Hi everyone.
Can it be shown that the logic linked to the SK-Loops technique is a logical subgroup of the more general MSLS's technique? If this were not the case, there are some examples of SK-loops that cannot be represented with an MSLS.
Ciao a Tutti
Paolo
SK-Loops and MSLS's
Re: SK-Loops and MSLS's
Hi Ajò,
I would say yes and no. Maybe. As far as I'm concerned, SK-Loop is a well-known and pretty well-defined Rank 0 pattern family, while MSLS is more of a fuzzy method to find certain types of Rank 0 patterns instead of a clear description of such patterns. To me MSLS seems so vaguely defined that I don't really know which patterns are definitely included and which are not.
However, I recall seeing that David himself (the creator of MSLS) considered things like Sue-de-Coqs as MSLS, so I guess it's pretty inclusive. Therefore I'm quite sure that SK-Loops should be included as well, because they're among the most easily recognizable non-trivial Rank 0 patterns. As far as I see, they can be described as both MSNS (cell truths) and MSHS (house truths) types of MSLS. For example, here's how I'd see the Easter Monster SK-Loop both ways:
As MSNS: (16x16 truths\links, Rank 0): {28N1379 1379N28 \ 38r2 45r8 48c2 39c8 27b19 16b37} => 13 eliminations
As MSHS: (16x16 truths\links, Rank 0): {1267R28 1267C28 \ 27b19 16b37 2n56 8n45 56n2 45n8} => 13 eliminations
Like I said, I don't really know if they're MSLS or not, but I don't much care either. They're valid Rank 0 patterns, which is all that matters. If someone spots them as SK-Loops, great. If someone spots them as MSLS, great. Personally I'm quite happy to deal with the generic set logic directly without any complicating layers on top of it. The only real value I see in MSLS is in its process which might help to spot some typical Rank 0 patterns. Personally I think it should stop there and use standard set logic notation (like I did above) to describe those found patterns instead of using a confusing hybrid approach David favored.
I'd also like to see an unambiguous definition of which Rank 0 patterns are actually counted as MSLS. Is it only those that have either all cells (MSNS) or all houses (MSHS) as truths or are more complicated combos included as well? Do houses include only rows and columns or are boxes included as well? I haven't seen these types of things specified anywhere, and I don't really like to deal with fuzzy concepts.
Ajò Dimonios wrote:Can it be shown that the logic linked to the SK-Loops technique is a logical subgroup of the more general MSLS's technique?
I would say yes and no. Maybe. As far as I'm concerned, SK-Loop is a well-known and pretty well-defined Rank 0 pattern family, while MSLS is more of a fuzzy method to find certain types of Rank 0 patterns instead of a clear description of such patterns. To me MSLS seems so vaguely defined that I don't really know which patterns are definitely included and which are not.
However, I recall seeing that David himself (the creator of MSLS) considered things like Sue-de-Coqs as MSLS, so I guess it's pretty inclusive. Therefore I'm quite sure that SK-Loops should be included as well, because they're among the most easily recognizable non-trivial Rank 0 patterns. As far as I see, they can be described as both MSNS (cell truths) and MSHS (house truths) types of MSLS. For example, here's how I'd see the Easter Monster SK-Loop both ways:
As MSNS: (16x16 truths\links, Rank 0): {28N1379 1379N28 \ 38r2 45r8 48c2 39c8 27b19 16b37} => 13 eliminations
As MSHS: (16x16 truths\links, Rank 0): {1267R28 1267C28 \ 27b19 16b37 2n56 8n45 56n2 45n8} => 13 eliminations
Like I said, I don't really know if they're MSLS or not, but I don't much care either. They're valid Rank 0 patterns, which is all that matters. If someone spots them as SK-Loops, great. If someone spots them as MSLS, great. Personally I'm quite happy to deal with the generic set logic directly without any complicating layers on top of it. The only real value I see in MSLS is in its process which might help to spot some typical Rank 0 patterns. Personally I think it should stop there and use standard set logic notation (like I did above) to describe those found patterns instead of using a confusing hybrid approach David favored.
I'd also like to see an unambiguous definition of which Rank 0 patterns are actually counted as MSLS. Is it only those that have either all cells (MSNS) or all houses (MSHS) as truths or are more complicated combos included as well? Do houses include only rows and columns or are boxes included as well? I haven't seen these types of things specified anywhere, and I don't really like to deal with fuzzy concepts.
-

SpAce - Posts: 2671
- Joined: 22 May 2017
Re: SK-Loops and MSLS's
Sk loop is a generic msls, where 4 digits locked in 16 cells over 4 sectors.
Its the easiest one to code for sure
Are they subgroups no, the difference between msls and sk loop is that a sk loop is defined by the original pattern.
Which is where msls advanced cases are derives, it can also find the smaller versions 2 digits 4 cells 2 sectors(xy loop)
Multifish/sharks on the other hand is a variation of msls using fish logic to prove the same eliminations as found by msls both of these are different on how they use data, end results are similar depending on the elimination routines programmed
Multi Fish limited to hidden sets (same as n fish)
Msls use a combination of hidden/naked marked as "home" or "away" to perform hidden or naked eliminations(see space comments)
Its the easiest one to code for sure
Are they subgroups no, the difference between msls and sk loop is that a sk loop is defined by the original pattern.
Which is where msls advanced cases are derives, it can also find the smaller versions 2 digits 4 cells 2 sectors(xy loop)
Multifish/sharks on the other hand is a variation of msls using fish logic to prove the same eliminations as found by msls both of these are different on how they use data, end results are similar depending on the elimination routines programmed
Multi Fish limited to hidden sets (same as n fish)
Msls use a combination of hidden/naked marked as "home" or "away" to perform hidden or naked eliminations(see space comments)
Some do, some teach, the rest look it up.
stormdoku
stormdoku
-

StrmCkr - Posts: 1513
- Joined: 05 September 2006
Re: SK-Loops and MSLS's
Hi StrmCkr.
So every Sk-Loop always implies an MSLS, even if its logic is apparently different and easier to program. This makes me deduce that an Almost (+1) Sk-Loop can always be replaced by an Almost-MSLS. In this way it is easy to demonstrate the property that reported PJP (PHILL) regarding the Almost (+1) Sk-Loop. http://forum.enjoysudoku.com/sk-and-related-loops-t35883.html.
Ciao a Tutti
Paolo
StrmCkr wrote:
Sk loop is a generic msls, where 4 digits locked in 16 cells over 4 sectors.
Its the easiest one to code for sure.
So every Sk-Loop always implies an MSLS, even if its logic is apparently different and easier to program. This makes me deduce that an Almost (+1) Sk-Loop can always be replaced by an Almost-MSLS. In this way it is easy to demonstrate the property that reported PJP (PHILL) regarding the Almost (+1) Sk-Loop. http://forum.enjoysudoku.com/sk-and-related-loops-t35883.html.
Ciao a Tutti
Paolo
- Ajò Dimonios
- Posts: 213
- Joined: 07 November 2019
Re: SK-Loops and MSLS's
StrmCkr wrote:Sk loop is a generic msls, where 4 digits locked in 16 cells over 4 sectors.
..
Are they subgroups no, the difference between msls and sk loop is that a sk loop is defined by the original pattern.
I see a bit of a contradiction in these two lines. Yeah, SK-Loops are not normally defined as MSLS (which I guess didn't even exist when SteveK made his discovery), but that doesn't stop seeing them as logical subtypes (i.e. subgroups) of the MSLS family (and it as a logical subtype of more generic Rank 0 patterns, etc). I thought that was what the OP asked.
It's a good question too. Someone should have constructed a logical hierarchy of all of these poorly defined types a long time ago. Learning them would be a zillion times easier if their mutual relationships were clearly defined. Now we probably have lots of people who think that SK-Loops, MSLS, Multi-Fish, and what not, are all somehow totally different patterns in a flat hierarchy, which simply isn't true. I know I was very confused for a long time, though I think I've slowly learned to see through the smoke and mirrors.
As far as I understand, those patterns are hierarchical, with MSLS on the top (most generic) and SK-Loop at the bottom (most specific). Both SK-Loops and Multi-Fish (that don't use cell truths) are subtypes of MSLS. As far as I understand, SK-Loops are also subtypes of Multi-Fish when seen as an MSHS. Here's my attempt to build such a hierarchy:
- Code: Select all
Alien Fish
|
---------+---------
| |
Rank 0 Rank 1+
|
-------------+------------
| |
MSLS other
|
--------------+----------------+
| |
MSNS MSHS
| |
-------+------- -----+---------+-------------
| | | | |
DDS other Multi-Fishes 1-digit-fishes other
| |
---+--- ---+---
| | | |
SK-Loop other SK-Loop other
--
Alien Fish : any {truths \ links} pattern using Allan Barker's generic set logic.
(optionally modified with Obi-Wahn's duplicates to avoid triplets)
Of course I don't know if it's at all correct, because neither MSLS nor Multi-Fish are clearly defined anywhere. I'm working on the assumption that MSNS includes patterns that have only cells as truths (with any link types) and MSHS includes patterns with only houses as truths (with any link types). Any mixed truth lists would be considered "other", including multi-fish that use cells as truths (dropping some of champagne's specimens out). If those rules are relaxed, there's no longer any logic in the hierarchy and it falls like a house of cards. (I'm fine with that option too, because then I just keep dealing with Alien Fishes directly.)
Now, even if that's somewhat correct, I have some specific questions left. Are MSLS so generic that they somehow include all Rank 0 patterns? If that's the case, then the first "other" should be moved one level lower next to MSHS. Even if that's not the case (my assumption), can we assume that all MSLS are strictly either MSNS or MSHS types (using my definitions above)? I think it makes the most sense, keeping the hierarchy simple and well-defined. I think the whole idea of such named subtypes should be that they're tightly defined patterns and possible to spot in the grid using relatively simple procedures. Anything more complex should be considered just generic Rank 0 patterns.
What do you think?
--
Edit. As I suspected, many of my assumptions were incorrect, as demonstrated by the following discussions. Here's a new diagram of my current understanding of the hierarchy.
Last edited by SpAce on Wed Dec 04, 2019 9:21 am, edited 1 time in total.
-

SpAce - Posts: 2671
- Joined: 22 May 2017
Re: SK-Loops and MSLS's
Ajò Dimonios wrote:This makes me deduce that an Almost (+1) Sk-Loop can always be replaced by an Almost-MSLS. In this way it is easy to demonstrate the property that reported PJP (PHILL) regarding the Almost (+1) Sk-Loop.
Did you read what I said about the almost-SK-Loop and its usefulness? Notice that Phil pretty much agreed. That approach wouldn't be very high on my list.
-

SpAce - Posts: 2671
- Joined: 22 May 2017
Re: SK-Loops and MSLS's
Hi all,
As reference.
Tarx0104
Above puzzle that Phil's solver cannot find SK loop, Exocet, MSLS. My post for this one here was lost in the May 2009 crash of the Players’ Forums.
For this one, my first post was based on viewing AALS(34578)r238c1 then after that Ronk & Allan Barker did show that using AAHS(14)r1256c1 is simpler.
Present as diagram: => r5c179<>6
The same way to eliminate: r5c139<>8 => (68)r5c46 and the puzzle downgrade to ER9.2
From Xsudo’s library (V.99m) based on AAHS(14)r1256c1
Tarx0104 56 Candidates, Raw Rank = 10 (linksets - sets)
17 Sets = {4R19 6R9 8R1 1468C1 468C5 1468C9 5N46}
27 Links = {4r257 6r3567 8r2568 16n1 27n5 46n9 1b1 4b159 6b567 8b356}
2 AURs = (84)R51C64, (64)R95C64 AUR points {aur 8r1c6 4r5c4 6r9c6 }
37 Eliminations, 1 Assignment --> r6c1<>1345, r2c468<>8, r5c179<>6, r5c139<>8, r7c246<>6, r1c1<>347, r3c67<>6, r4c45<>6, r4c45<>8, r5c46<>4, r6c57<>6, r6c58<>8, r8c34<>8, r46c9<>4, r1c2<>1, r6c9<>5, r1c1=1
P/s: I don't know there are some puzzles on hardest list like this one (except tarx0105) or not


totuan
As reference.
Tarx0104
- Code: Select all
000050009006000100089100040200005000090010030000207000001000800040001060900020017
Above puzzle that Phil's solver cannot find SK loop, Exocet, MSLS. My post for this one here was lost in the May 2009 crash of the Players’ Forums.
For this one, my first post was based on viewing AALS(34578)r238c1 then after that Ronk & Allan Barker did show that using AAHS(14)r1256c1 is simpler.
- Code: Select all
*-----------------------------------------------------------------------------*
| 1347 1237 2347 | 34678 5 23468 | 2367 278 9 |
| 3457 2357 6 | 34789 34789 23489 | 1 2578 2358 |
| 357 8 9 | 1 367 236 | 23567 4 2356 |
|-------------------------+-------------------------+-------------------------|
| 2 1367 3478 | 34689 34689 5 | 4679 789 1468 |
| 45678 9 4578 | 468 1 468 | 24567 3 24568 |
| 134568 1356 3458 | 2 34689 7 | 4569 589 14568 |
|-------------------------+-------------------------+-------------------------|
| 3567 23567 1 | 345679 34679 3469 | 8 259 2345 |
| 3578 4 23578 | 35789 3789 1 | 2359 6 235 |
| 9 356 358 | 34568 2 3468 | 345 1 7 |
*-----------------------------------------------------------------------------*
Present as diagram: => r5c179<>6
- Code: Select all
AALS(34578)r238c1 A*ALS(45678)r5c146
|| ||
(357)r238c1--(357=6)r7c1-----(6)r5c1
|| | ||
|| -----------------(57)r5c1
|| ||
|| (468)r5c146*
||
(4)r2c1-----(4)r2c5
|| | ||
|| | (4)r46c5-(4=68)r5c46*
|| | ||
|| | (4)r7c5----------(4)r7c9-----------------------------------
|| | || |
|| | AUR(48)r15c46 || |
|| | || || |
|| ----(4)r1c13 || |
|| || || |
|| (6)r5c46* || |
|| || || |
|| (8)r1c8----------(8)r2c9 A*ALS(24568)r5c146 |
|| | || || |
|| | (235)r278c9--(235=6)r3c9-(6)r5c9 |
|| | || | || |
|| | || -------------(25)r5c9 |
|| | || || |
|| | AALS(23458)r278c9 (468)r5c469* |
|| | |
(8)r8c1-----(8)r8c5 | (4)r7c5-----------------------------------
|| | ||
(8)r2c5----------(4)r2c5
|| ||
|| (4)r46c5-(4=68)r5c46*
||
(8)r46c5-(8=46)r5c46*
The same way to eliminate: r5c139<>8 => (68)r5c46 and the puzzle downgrade to ER9.2
From Xsudo’s library (V.99m) based on AAHS(14)r1256c1
Tarx0104 56 Candidates, Raw Rank = 10 (linksets - sets)
17 Sets = {4R19 6R9 8R1 1468C1 468C5 1468C9 5N46}
27 Links = {4r257 6r3567 8r2568 16n1 27n5 46n9 1b1 4b159 6b567 8b356}
2 AURs = (84)R51C64, (64)R95C64 AUR points {aur 8r1c6 4r5c4 6r9c6 }
37 Eliminations, 1 Assignment --> r6c1<>1345, r2c468<>8, r5c179<>6, r5c139<>8, r7c246<>6, r1c1<>347, r3c67<>6, r4c45<>6, r4c45<>8, r5c46<>4, r6c57<>6, r6c58<>8, r8c34<>8, r46c9<>4, r1c2<>1, r6c9<>5, r1c1=1
P/s: I don't know there are some puzzles on hardest list like this one (except tarx0105) or not
totuan
- totuan
- Posts: 272
- Joined: 25 May 2010
- Location: vietnam
Re: SK-Loops and MSLS's
Hi totuan! Good to see you still here!
Very nice! I'm still wondering about how you actually find such complex yet neat moves, and can also notate them so cleanly. Impressive as usual!
Is that possible??? Wow. So the raw rank is 10, yet it can get all those eliminations as if they were Rank 0? It must have some serious triplet magic going on. I can't say that I can see how it all works but I trust it does if you say so.
I can see the URs but what does "AUR points" mean? How are the URs actually integrated with the set logic here? I've never used XSudo, but based on the documentation I've thought that their guardians would be added as a virtual set (with corresponding links). Apparently that's not exactly how it works here. Can you explain this part a bit more? Personally I might have seen something like this as a virtual set: {4r1c13 4r9c7 6r9c2 8r1c8}.
totuan wrote:Present as diagram: => r5c179<>6
The same way to eliminate: r5c139<>8 => (68)r5c46 and the puzzle downgrade to ER9.2
Very nice! I'm still wondering about how you actually find such complex yet neat moves, and can also notate them so cleanly. Impressive as usual!
From Xsudo’s library (V.99m) based on AAHS(14)r1256c1
Tarx0104 56 Candidates, Raw Rank = 10 (linksets - sets)
...
37 Eliminations, 1 Assignment --> r6c1<>1345, r2c468<>8, r5c179<>6, r5c139<>8, r7c246<>6, r1c1<>347, r3c67<>6, r4c45<>6, r4c45<>8, r5c46<>4, r6c57<>6, r6c58<>8, r8c34<>8, r46c9<>4, r1c2<>1, r6c9<>5, r1c1=1
Is that possible??? Wow. So the raw rank is 10, yet it can get all those eliminations as if they were Rank 0? It must have some serious triplet magic going on. I can't say that I can see how it all works but I trust it does if you say so.
17 Sets = {4R19 6R9 8R1 1468C1 468C5 1468C9 5N46}
27 Links = {4r257 6r3567 8r2568 16n1 27n5 46n9 1b1 4b159 6b567 8b356}
2 AURs = (84)R51C64, (64)R95C64 AUR points {aur 8r1c6 4r5c4 6r9c6 }
I can see the URs but what does "AUR points" mean? How are the URs actually integrated with the set logic here? I've never used XSudo, but based on the documentation I've thought that their guardians would be added as a virtual set (with corresponding links). Apparently that's not exactly how it works here. Can you explain this part a bit more? Personally I might have seen something like this as a virtual set: {4r1c13 4r9c7 6r9c2 8r1c8}.
-

SpAce - Posts: 2671
- Joined: 22 May 2017
Re: SK-Loops and MSLS's
Hi SpAce,
Thanks, perhaps I was just lucky
I don’t know, Allan’s solver do that. My moves only 06 eliminations
Again, Allan’s solver do that. But as a habit I usually use AUR instead of UR and I don't remember some name of techniques.
For Xsudo, you can see on Allan’s solver that download here . I don’t study how Allan’s solver works so I cannot explain for you more, sorry about that.
P/s: I think puzzles with base like (468)r5c46 in tarx0104 can solve the same way, but I have not yet study more...
totuan
SpAce wrote:Very nice! I'm still wondering about how you actually find such complex yet neat moves, and can also notate them so cleanly. Impressive as usual!
Thanks, perhaps I was just lucky
SpAce wrote:From Xsudo’s library (V.99m) based on AAHS(14)r1256c1
Tarx0104 56 Candidates, Raw Rank = 10 (linksets - sets)
...
37 Eliminations, 1 Assignment --> r6c1<>1345, r2c468<>8, r5c179<>6, r5c139<>8, r7c246<>6, r1c1<>347, r3c67<>6, r4c45<>6, r4c45<>8, r5c46<>4, r6c57<>6, r6c58<>8, r8c34<>8, r46c9<>4, r1c2<>1, r6c9<>5, r1c1=1
Is that possible??? Wow. So the raw rank is 10, yet it can get all those eliminations as if they were Rank 0? It must have some serious triplet magic going on. I can't say that I can see how it all works but I trust it does if you say so.
I don’t know, Allan’s solver do that. My moves only 06 eliminations
SpAce wrote:I can see the URs but what does "AUR points" mean?
Again, Allan’s solver do that. But as a habit I usually use AUR instead of UR and I don't remember some name of techniques.
SpAce wrote: How are the URs actually integrated with the set logic here? I've never used XSudo, but based on the documentation I've thought that their guardians would be added as a virtual set (with corresponding links). Apparently that's not exactly how it works here. Can you explain this part a bit more? Personally I might have seen something like this as a virtual set: {4r1c13 4r9c7 6r9c2 8r1c8}.
For Xsudo, you can see on Allan’s solver that download here . I don’t study how Allan’s solver works so I cannot explain for you more, sorry about that.
P/s: I think puzzles with base like (468)r5c46 in tarx0104 can solve the same way, but I have not yet study more...
totuan
- totuan
- Posts: 272
- Joined: 25 May 2010
- Location: vietnam
Re: SK-Loops and MSLS's
correctAUR should mean Almost Unique Rectangle.
Some do, some teach, the rest look it up.
stormdoku
stormdoku
-

StrmCkr - Posts: 1513
- Joined: 05 September 2006
Re: SK-Loops and MSLS's
totuan wrote:Thanks, perhaps I was just lucky
Somehow I don't think that's the reason
For Xsudo, you can see on Allan’s solver that download here .
I would have downloaded it a long time ago, but I'm a Mac user. I should probably install Windows in a virtual machine, but I haven't got around to do that because I have no other use for it. I guess XSudo would be a good enough reason, though. It can clearly perform miracles, so there would be much to learn, I'm sure, even if a lot of it is not really humanly applicable.
-

SpAce - Posts: 2671
- Joined: 22 May 2017
Re: SK-Loops and MSLS's
Hi creint,
Thanks! I appreciate it.
Yes, I know. It's an obsolete name from the days when UR was interpreted to mean just the deadly rectangle itself. The modern meaning of UR is exactly the same as what AUR used to mean (i.e. deadly rectangle + guardians), though it's sometimes used in its old meaning too. None of that makes a lot of sense, actually, but it is what it is.
Anyway, it's better to use just UR these days to avoid more confusion. No player in the forum Puzzles section calls anything "AUR", and if someone does, it raises eyebrows. Personally I use "UR" to mean the full pattern (with guardians), and sometimes "DR" to refer to the deadly rectangle alone if it needs to be isolated for some reason (rarely). That makes the most sense to me, if you think about the names.
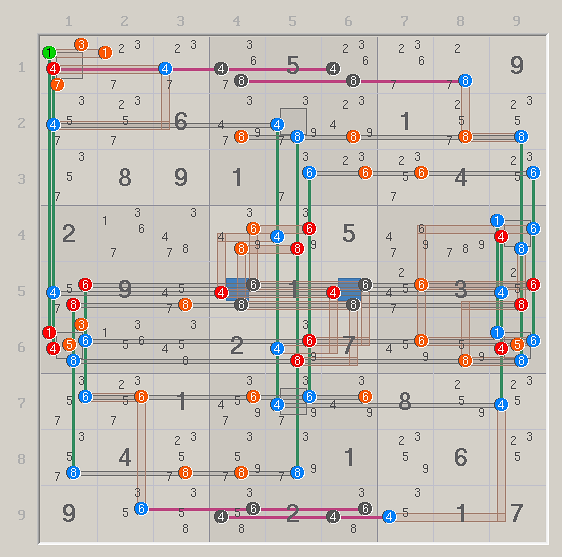
Anyway, I'm just wondering how exactly XSudo used the (A)URs here, but I'll try and figure it out. Maybe your picture helps!
--
Added. Looks like I found some relevant background information from A.B. himself that might help too.
creint wrote:An image for Space.
Thanks! I appreciate it.
AUR should mean Almost Unique Rectangle.
Yes, I know. It's an obsolete name from the days when UR was interpreted to mean just the deadly rectangle itself. The modern meaning of UR is exactly the same as what AUR used to mean (i.e. deadly rectangle + guardians), though it's sometimes used in its old meaning too. None of that makes a lot of sense, actually, but it is what it is.
Anyway, it's better to use just UR these days to avoid more confusion. No player in the forum Puzzles section calls anything "AUR", and if someone does, it raises eyebrows. Personally I use "UR" to mean the full pattern (with guardians), and sometimes "DR" to refer to the deadly rectangle alone if it needs to be isolated for some reason (rarely). That makes the most sense to me, if you think about the names.
Anyway, I'm just wondering how exactly XSudo used the (A)URs here, but I'll try and figure it out. Maybe your picture helps!
--
Added. Looks like I found some relevant background information from A.B. himself that might help too.
-

SpAce - Posts: 2671
- Joined: 22 May 2017
Re: SK-Loops and MSLS's
Hi Paolo
Your original question comes down to what you regard as an SK loop and what you regard as an MSLS. For example, I have found that all "vanilla" SK loops (all links double) have a corresponding MSLS. However, variant SK loops, a large number of which are on my website, mostly don't. In contrast, a great many of the MSLS's that I have documented do not have an SK loop.
I agree that MSLS's are not well defined, and I can't claim my coding is anything special, so when I say I don't find them in puzzles with variant SK loops, perhaps someone else will.
Cheers, Phil
Your original question comes down to what you regard as an SK loop and what you regard as an MSLS. For example, I have found that all "vanilla" SK loops (all links double) have a corresponding MSLS. However, variant SK loops, a large number of which are on my website, mostly don't. In contrast, a great many of the MSLS's that I have documented do not have an SK loop.
I agree that MSLS's are not well defined, and I can't claim my coding is anything special, so when I say I don't find them in puzzles with variant SK loops, perhaps someone else will.
Cheers, Phil
- pjb
- 2014 Supporter
- Posts: 2749
- Joined: 11 September 2011
- Location: Sydney, Australia
Re: SK-Loops and MSLS's
Hi Phil,
Good of you to chime in.
Exactly. It's an unfortunate situation that exact definitions are lacking for some of the most important advanced patterns. That said, I actually found a relatively decent definition of Multi-Fish, so I have to (at least partly) absolve champagne In fact, I would suggest that you'd add that (or a similar definition) to your Multi-Fish help file, because now it only describes (and links to) David's search procedure (part of MSLS) which is not a definition of multi-fish at all. That's quite confusing, actually, because it mixes the concepts of multi-fish and MSLS without defining either. Besides, it kind of gives the false idea that David invented the multi-fish concept itself. Similarly, your help file for MSLS doesn't define it at all, but links to David's shark thread which must be the most confusing piece I've read on the forum. (Then again, I guess there's no good definition of MSLS anywhere to link to.)
In fact, I would suggest that you'd add that (or a similar definition) to your Multi-Fish help file, because now it only describes (and links to) David's search procedure (part of MSLS) which is not a definition of multi-fish at all. That's quite confusing, actually, because it mixes the concepts of multi-fish and MSLS without defining either. Besides, it kind of gives the false idea that David invented the multi-fish concept itself. Similarly, your help file for MSLS doesn't define it at all, but links to David's shark thread which must be the most confusing piece I've read on the forum. (Then again, I guess there's no good definition of MSLS anywhere to link to.)
I hope you take those comments as very friendly and constructive criticism! I'm sure we're all grateful for your awesome solver that has these patterns covered at all!
They do, as far as I understand.
I would probably see it exactly the other way. Based on a very small sample size, many of them probably wouldn't make any sense to me as loops. On the other hand, I would probably see all of them as MSLS -- the way I understand that poorly defined concept. For example, if I take your first variant example:
I really don't see any loop there (yes, I understand how you see it), but it's easy as a cell-based Rank 0 pattern:
16x16 Alien Fish (Rank 0): {47N1289 5689N37 \ 1r47 1c7 7c3 3b469 46b67 5b49 9b479} => 11 eliminations (same as your "variant SK Loop")
Now, is that not a Multi-Sector Naked Set (all base sets being cells), in other words one of the two types of MSLS patterns? Or is there a more restrictive definition somewhere?
That must certainly be true, SK-Loop being the rarest and the most specific named Rank 0 pattern.
Glad to hear that I'm not alone with that view! Well, actually I'm not that glad, because I was hoping you'd have some insider information having personally discussed it with David when implementing your code. I've seen bits and pieces around the forum, and based on those I've tried to gain an idea, but it's far from clear. I really haven't seen anywhere any kind of a complete definition of MSLS, just examples of it. And, since I can't (under)stand David's "simplified" notations and the whole concept of "truth balancing" (supposedly simple too), I pretty much skip them unless I bother to convert them into standard truths and links (which I find easy to understand -- unless they're like totuan's example).
I'm thinking the whole idea probably started as David's private synonym for DDS which he called DLS (without really acknowledging they were the same thing -- only that his chosen name was better). Then, at some unknown point in time he apparently extended it with multiple houses per digit (already envisioned and implemented by Obi-Wahn in the DDS thread), as well as the hidden side of things (also not a new idea), and started calling it MSLS, including the complementary MSNS and MSHS points of view. Only there's no clear documentation of what they're supposed to mean and include exactly. One can only deduce from posts like this, this, this, and this, that the concept is pretty inclusive. Then came "sharks", and soon the whole MSLS thing started to revolve around them and "truth balancing" and search procedures for multi-fish, blurring any chance of clearer definitions for the actually included (and not included) patterns.
That's my biggest problem with the whole MSLS thing -- on the one hand it's supposedly a type of pattern but it's actually defined as a fuzzy (but apparently effective) search procedure only (as far as I know). They should be two completely separate things, each defined on its own -- especially since the search procedure probably doesn't find all types of patterns that apparently should be included under the MSLS umbrella (based on the observations above). One should be able to look for MSLS patterns any way they like and know with certainty when they've found one (or not), without needing to know anything about "home" and "away" sets etc. Similarly one should be able to use David's clever search algorithm and use any applicable name and notation for the found patterns. Now the two concepts are neatly mixed up, like good old spaghetti code.
Anyway, based on those little pieces, my current take is that MSNS is any Rank 0 pattern with only cells as base sets (and obviously houses as covers), i.e. extended DDS, while MSHS is any Rank 0 pattern with only houses as base sets (and anything as covers) -- including most (at least row/col-based) multi-fish without base-cells. Is that anywhere close to the truth? Who the hell knows, but I can't think of any other clear-cut definition that would make sense to me. Are there MSLS patterns with mixed sets as bases? I have no idea. I do know that champagne's multi-fish do include such things. Are they counted as MSLS patterns too? If so, then I don't think they can be purely MSHS types.
Based on those presumed definitions, it seems to me that your implementation covers most of the complicated MSNS types (as MSLS), while most of the complicated MSHS types are found as Multifish. What it probably doesn't cover is the simpler types that are usually seen as other patterns (such as Sue de Coq), and apparently also some more complicated types (that are for example found as "variant SK-Loops"). But, I could be completely wrong... That's just the way it seems to me based on a very small sample size and limited understanding.
Last but not least, I don't want this to sound like I'm bashing David. After all, I'm possibly the only avid and grateful user of GEM. His work on the JExocet is obviously extraordinary, and I'm sure his MSLS/multi-fish search procedure is very clever. He just didn't do a very good job of separating procedure from pattern, so now it seems that no one has a clear idea of what patterns are actually counted (and not) as MSLS.
Good of you to chime in.
pjb wrote:Your original question comes down to what you regard as an SK loop and what you regard as an MSLS.
Exactly. It's an unfortunate situation that exact definitions are lacking for some of the most important advanced patterns. That said, I actually found a relatively decent definition of Multi-Fish, so I have to (at least partly) absolve champagne
I hope you take those comments as very friendly and constructive criticism! I'm sure we're all grateful for your awesome solver that has these patterns covered at all!
For example, I have found that all "vanilla" SK loops (all links double) have a corresponding MSLS.
They do, as far as I understand.
However, variant SK loops, a large number of which are on my website, mostly don't.
I would probably see it exactly the other way. Based on a very small sample size, many of them probably wouldn't make any sense to me as loops. On the other hand, I would probably see all of them as MSLS -- the way I understand that poorly defined concept. For example, if I take your first variant example:
- Code: Select all
....1.......234.....15.62....2.7.8...6.....9.4.......5..8.2.7...5.....6.3.......4
I really don't see any loop there (yes, I understand how you see it), but it's easy as a cell-based Rank 0 pattern:
16x16 Alien Fish (Rank 0): {47N1289 5689N37 \ 1r47 1c7 7c3 3b469 46b67 5b49 9b479} => 11 eliminations (same as your "variant SK Loop")
Now, is that not a Multi-Sector Naked Set (all base sets being cells), in other words one of the two types of MSLS patterns? Or is there a more restrictive definition somewhere?
In contrast, a great many of the MSLS's that I have documented do not have an SK loop.
That must certainly be true, SK-Loop being the rarest and the most specific named Rank 0 pattern.
I agree that MSLS's are not well defined
Glad to hear that I'm not alone with that view! Well, actually I'm not that glad, because I was hoping you'd have some insider information having personally discussed it with David when implementing your code. I've seen bits and pieces around the forum, and based on those I've tried to gain an idea, but it's far from clear. I really haven't seen anywhere any kind of a complete definition of MSLS, just examples of it. And, since I can't (under)stand David's "simplified" notations and the whole concept of "truth balancing" (supposedly simple too), I pretty much skip them unless I bother to convert them into standard truths and links (which I find easy to understand -- unless they're like totuan's example).
I'm thinking the whole idea probably started as David's private synonym for DDS which he called DLS (without really acknowledging they were the same thing -- only that his chosen name was better). Then, at some unknown point in time he apparently extended it with multiple houses per digit (already envisioned and implemented by Obi-Wahn in the DDS thread), as well as the hidden side of things (also not a new idea), and started calling it MSLS, including the complementary MSNS and MSHS points of view. Only there's no clear documentation of what they're supposed to mean and include exactly. One can only deduce from posts like this, this, this, and this, that the concept is pretty inclusive. Then came "sharks", and soon the whole MSLS thing started to revolve around them and "truth balancing" and search procedures for multi-fish, blurring any chance of clearer definitions for the actually included (and not included) patterns.
That's my biggest problem with the whole MSLS thing -- on the one hand it's supposedly a type of pattern but it's actually defined as a fuzzy (but apparently effective) search procedure only (as far as I know). They should be two completely separate things, each defined on its own -- especially since the search procedure probably doesn't find all types of patterns that apparently should be included under the MSLS umbrella (based on the observations above). One should be able to look for MSLS patterns any way they like and know with certainty when they've found one (or not), without needing to know anything about "home" and "away" sets etc. Similarly one should be able to use David's clever search algorithm and use any applicable name and notation for the found patterns. Now the two concepts are neatly mixed up, like good old spaghetti code.
Anyway, based on those little pieces, my current take is that MSNS is any Rank 0 pattern with only cells as base sets (and obviously houses as covers), i.e. extended DDS, while MSHS is any Rank 0 pattern with only houses as base sets (and anything as covers) -- including most (at least row/col-based) multi-fish without base-cells. Is that anywhere close to the truth? Who the hell knows, but I can't think of any other clear-cut definition that would make sense to me. Are there MSLS patterns with mixed sets as bases? I have no idea. I do know that champagne's multi-fish do include such things. Are they counted as MSLS patterns too? If so, then I don't think they can be purely MSHS types.
Based on those presumed definitions, it seems to me that your implementation covers most of the complicated MSNS types (as MSLS), while most of the complicated MSHS types are found as Multifish. What it probably doesn't cover is the simpler types that are usually seen as other patterns (such as Sue de Coq), and apparently also some more complicated types (that are for example found as "variant SK-Loops"). But, I could be completely wrong... That's just the way it seems to me based on a very small sample size and limited understanding.
Last but not least, I don't want this to sound like I'm bashing David. After all, I'm possibly the only avid and grateful user of GEM. His work on the JExocet is obviously extraordinary, and I'm sure his MSLS/multi-fish search procedure is very clever. He just didn't do a very good job of separating procedure from pattern, so now it seems that no one has a clear idea of what patterns are actually counted (and not) as MSLS.
-

SpAce - Posts: 2671
- Joined: 22 May 2017