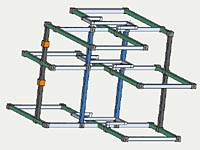
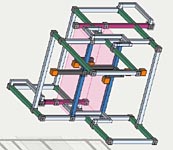
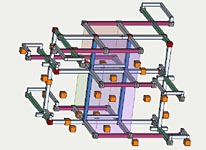
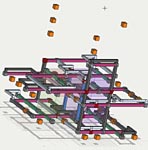
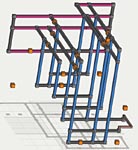
More Monster Loops, Structure and Symmetry
Fata Morgana, Platinum Blond, structure and symmetry
A lot of information has come out about large symmetrical loops in monster puzzles since the initial discovery of the SK loop. Trying to see how the pieces fit together, I have come across a few possibly interesting points. Although the following relates to a number of threads, it doesn't really fit any so pardon the new thread. One relevant thread is Champagne's most recent bi bi pattern in hardest puzzles. Another is The Illusion of Fata Morgana
Two puzzles in particular make good examples, Fata Morgana, and Platinum Blond. One because it has been well studied and the other because it has not. The following examples are included in a somewhat logical order.
(EM=Easter Monster, FM=Fata Morgana, PB=Platinum Blond)
EM Easter Monster and the SK Loop
FM Original Loop-1, BB Sets
FM Applying ttt's AUR Solution
FM Combining ttt's AUR and Original Loop 1
FM Loop 2, Additional Constraints
FM Full Loop Solution
PB Initial Loop
PB Initial Loop Morph
PB Full Solution with AURs
PB What is This?
More Monster Loops, Structure and Symmetry
22 posts
• Page 1 of 2 • 1, 2
More Monster Loops, Structure and Symmetry
by Allan Barker » Sat Jan 17, 2009 2:15 am
Last edited by Allan Barker on Thu Jan 29, 2009 9:03 am, edited 5 times in total.
- Allan Barker
- Posts: 266
- Joined: 20 February 2008
by Allan Barker » Sat Jan 17, 2009 2:17 am
Some Relavant Information
AURs, Uniqueness and Sudoku Set Logic
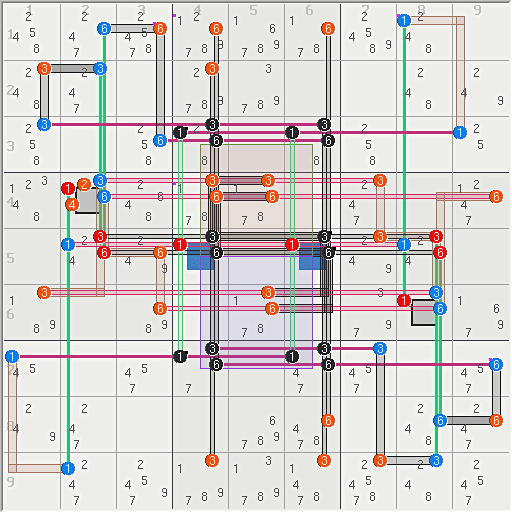
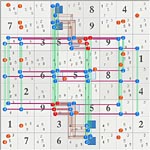
After some effort, I recently added uniqueness capabilities to my set solver/analyzer. This integrates AURs and MUGs as logical entities to the existing set and linkset logic. Once a UR is designated, the software can use any combination of sets to implement strong inferences derived from multiple UR constraints. This allows UR and uniqueness to be used during searches. In diagrams, a UR is rectangle and usually 4 additional base sets that contain the derived strong inference. This is logically the same as common AUR usage and notationally consistent with the set logic.
Key to grids
Solid, colored lines/bars are base (constraint) sets.
Hollow, shaded lines/bars are weak cover (constraint) sets.
Eliminated candidates are orange/red
Black Shaded cover sets are Rank 0, like those of a continuous NL or most fish.
MUGs are made of multiple 8 candidate AURs.
AURs, Uniqueness and Sudoku Set Logic
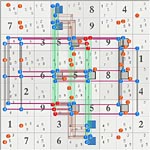
After some effort, I recently added uniqueness capabilities to my set solver/analyzer. This integrates AURs and MUGs as logical entities to the existing set and linkset logic. Once a UR is designated, the software can use any combination of sets to implement strong inferences derived from multiple UR constraints. This allows UR and uniqueness to be used during searches. In diagrams, a UR is rectangle and usually 4 additional base sets that contain the derived strong inference. This is logically the same as common AUR usage and notationally consistent with the set logic.
Key to grids
Solid, colored lines/bars are base (constraint) sets.
Hollow, shaded lines/bars are weak cover (constraint) sets.
Eliminated candidates are orange/red
Black Shaded cover sets are Rank 0, like those of a continuous NL or most fish.
MUGs are made of multiple 8 candidate AURs.
- Allan Barker
- Posts: 266
- Joined: 20 February 2008
by Allan Barker » Sat Jan 17, 2009 2:19 am
Some Logical Processes in Monster Puzzles
EM Easter Monster and the SK Loop
The original SK loop from Easter Monster uses 16 base sets and 16 cover sets to make what is logically equivalent to a continuous nice loop. All 13 eliminations occur because all the cover sets are rank 0.
16 Sets = {1267R2 1267R8 1267C2 1267C8}
16 Links = {56n2 8n4 28n5 2n6 45n8 1b37 2b19 6b37 7b19}
13 Eliminations
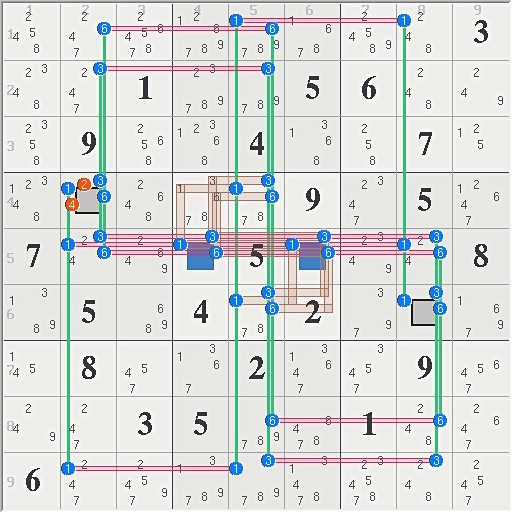
FM Original Loop-1 and BB (bi-bi) Sets
The first and easiest to find FM loop uses 3 floors of digits 136. It is the simplest example of a BB pattern with the first bi- pair in r5c46 (strong sets) and the second -bi pair in r4c2 and r6c8 (weak sets). The weak sets are highlighted black because they are rank 0 and can thus cause eliminations. The weak links in bi-bi groups are almost always rank 0, which is often not true of other weak links in the pattern.
11 Sets = {1C258 3C258 6C258 5N46}
14 Links = {1r159 3r259 6r158 4n2 6n8 136b5}
2 Eliminates = r4c2<>24
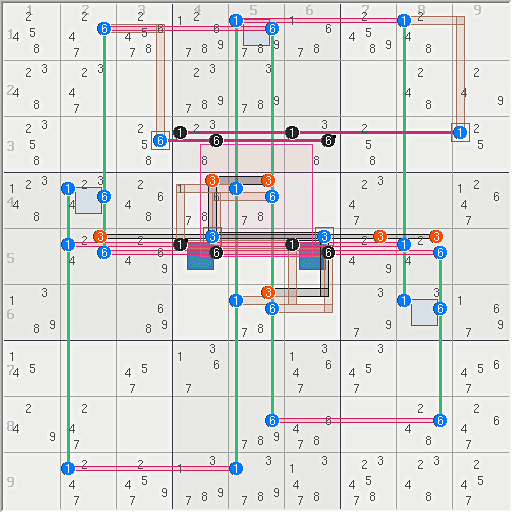
FM Applying ttt's AUR Solution
This is ttt's first solution AURhere that uses digit levels 1 and 6 and an AUR in r35c46. that combines with the loops on levels 1 and 6 to force 3r5c46 true, which eliminates the 6 3s in sets 3r5 and 3b5. Note: that ttt's AUR requires a weak cell set in r1c5 (which is in his diagram!) The BB pattern is not functional because there is no loop or other logic in the level 3 floor thus BB sets r4c2 and r6c8 are not rank 0.
10 Sets = {16R3 1C258 6C258 5N46}
15 Links = {1r159 3r5 6r158 4n2 1n5 6n8 6b1 1b3 136b5}
1 AUR = (16)r35c46
6 Eliminates = r4c45<>3, r5c278<>3, r6c5<>3
FM Combining ttt's AUR and Original Loop 1
If the AUR solution is combined with the original loop, several more eliminations appear including those in r4c2<>24 and 5 new digit 3 eliminations. The 5 new digit 3 eliminations occur because the AUR forces the entire level 3 floor to rank 0, as noted by the black cover-set highlights. There are now 13 eliminations.
13 Sets = {16R3 1C258 3C258 6C258 5N46}
17 Links = {1r159 3r259 6r158 4n2 1n5 6n8 6b1 1b3 136b5}
1 AUR = (16)r35c46
13 Eliminations = r2c14<>3, r4c2<>24, r4c45<>3, r5c278<>3, r6c5<>3, r9c467<>3
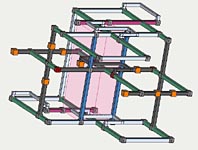
FM Loop 2, Additional Constraints
The AUR above uses 2 row base sets 16R3 as part of its strong inference. The original FM Loop-2 below uses 6 column bases sets and 6 row base sets that include 16R3 used by the AUR. This loop eliminates 24r4c2 and 6 additional candidates in levels 3 and 6. The extra eliminations occur because 4 extra cell link sets in r37c46 introduce new constraints that make levels 3 and 6 rank 0. These 4 cell sets are not used to cover the logic and are not considered cover sets.
14 Sets = {136R3 136R7 136C2 136C8 5N46}
21 Links = {136r5 136c4 136c6 4n2 37n4 37n6 6n8 1b37 3b19 6b19}
8 Eliminations = r1c3<>6, r2c1<>3, r4c2<>2, r4c2<>4, r5c3<>6, r5c7<>3, r8c9<>6, r9c7<>3
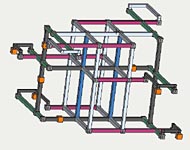
FM Full Loop Solution
What happens if the AUR is integrated with the FM Loop 2? The initial answer is nothing unless all of the Loop 1 base sets are added, which will cause 15 eliminations.
However, Loop 2 defines an inner rectangle whose corners are r37c46. This rectangle also encloses 4 possible AURs. When all 4 AUR are added to the Loop 2 logic the result now produces 32 eliminations all based on the original 14 base sets, and no further integration produces additional eliminations. This pretty much destroys FM .
14 Sets = {136R3 136R7 136C2 136C8 5N46}
27 Links = {1r5 3r456 6r456 136c4 136c6 4n2 6n8 1b37 3b14569 6b14569}
4 AURs = (13)r35c46 + (16)r35c46 + (13)r57c46 + (16)r57c46
32 Eliminations
Platinum Blond
Platinum Blond makes a good comparison because it is both different and difficult. It does not share the same symmetry as many other puzzles however, like Golden Nugget, it can be morphed to a more symmetric form. Platinum Blond is also short because it uses floors 678 making it very short in 3D images. Platinum Blond also has some surprises.
PB Initial Loop
An initial search on PB shows a loop similar to Golden Nugget with a pair of strong cell sets (BB pattern) in box 3. However, it has 3 weak cell sets that are all rank 0 and cause eliminations. This is perhaps a bi-tri. Once major difference is the pattern uses a digit 4 base set. This loop makes 6 eliminations.
12 Sets = {679R3 679R4 4679R7 12N7}
15 Links = {6c157 7c167 9c257 47n8 7n9 679b3}
6 Eliminations = r4c8<>234, r7c8<>231
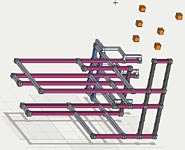
PB Initial Loop Morph
Platinum Blond is morphed to a form similar to FM and 4 AURs are added to the same locations that were used in FM.
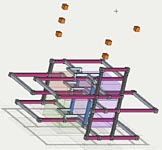
PB Full Solution, 36 Eliminations
A search discovers a solution of the same type as the FM full loop solution above, which uses all the same logical methods. This results in 36 eliminations.
18 Sets = {679R2 679R5 4679R8 679C3 679C7 46N5}
29 Links = {7r7 4c4 6c158 7c459 9c2458 28n4 8n6 4b8 6b357 7b14589 9b15689}
4 AURs = (67)r46c35 + (69)r46c35 + (67)r46c57 + (69)r46c57
36 Eliminations =
r2c4<>2, r2c4<>3, r2c4<>4, r2c4<>6, r2c5<>7, r2c5<>9, r3c1<>7, r3c5<>7,
r4c1<>7, r4c2<>9, r4c5<>6, r4c8<>9, r4c9<>7, r5c4<>7, r5c4<>9, r5c6<>7,
r5c6<>9, r6c1<>7, r6c2<>9, r6c4<>7, r6c4<>9, r6c5<>6, r6c8<>9, r6c9<>7,
r7c4<>7, r7c9<>7, r8c4<>2, r8c4<>3, r8c4<>6, r8c5<>7, r8c5<>9, r8c6<>1, r8c6<>6, r9c4<>9, r9c5<>9,r9c8<>9
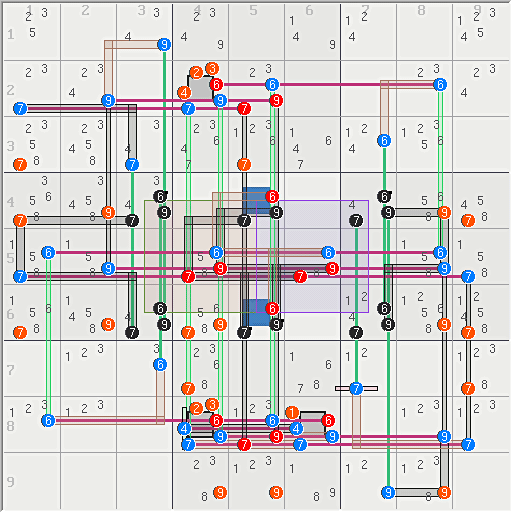
PB What is This? 17 More Eliminations
However, the Platinum Blond story is not finished, as perhaps that of other monsters. The following 17 eliminations are from completely different logic, which is also not based on floors. It has some resemblance to and SK loop because it is rank 0 with equal numbers of base and cover sets however, it is geometrically different from an SK loop and cannot be morphed into one.
It is made of from hidden and naked AALS and one additional set.
1) A hidden row AALS (4 rows with digits in 6 columns) in row 1.
2) An AALS in row 3. (digits 123467)
3) An AALS in row 7 (digits 123678)
4) An AALS in row 9 (digits 12389)
5) A box set 8B9.
16 Sets = {1235R1 3N3467 7N3467 9N467 8B9}
16 Links = {467r3 678r7 89r9 1c67 2c47 3c34 1n19}
17 ELiminations = r1c9<>4, r2c4<>23, r3c15<>7, r3c2<>4, r3c58<>6,
r4c3<>3, r6c7<>12, r7c9<>7, r8c4<>23, r8c6<>1, r9c58<>9
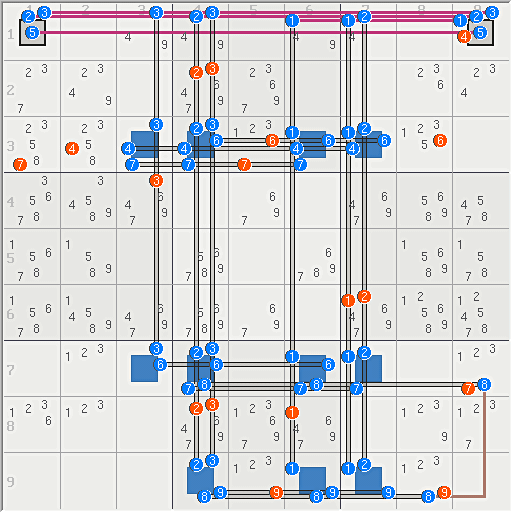
EM Easter Monster and the SK Loop
The original SK loop from Easter Monster uses 16 base sets and 16 cover sets to make what is logically equivalent to a continuous nice loop. All 13 eliminations occur because all the cover sets are rank 0.
16 Sets = {1267R2 1267R8 1267C2 1267C8}
16 Links = {56n2 8n4 28n5 2n6 45n8 1b37 2b19 6b37 7b19}
13 Eliminations
FM Original Loop-1 and BB (bi-bi) Sets
The first and easiest to find FM loop uses 3 floors of digits 136. It is the simplest example of a BB pattern with the first bi- pair in r5c46 (strong sets) and the second -bi pair in r4c2 and r6c8 (weak sets). The weak sets are highlighted black because they are rank 0 and can thus cause eliminations. The weak links in bi-bi groups are almost always rank 0, which is often not true of other weak links in the pattern.
11 Sets = {1C258 3C258 6C258 5N46}
14 Links = {1r159 3r259 6r158 4n2 6n8 136b5}
2 Eliminates = r4c2<>24
FM Applying ttt's AUR Solution
This is ttt's first solution AURhere that uses digit levels 1 and 6 and an AUR in r35c46. that combines with the loops on levels 1 and 6 to force 3r5c46 true, which eliminates the 6 3s in sets 3r5 and 3b5. Note: that ttt's AUR requires a weak cell set in r1c5 (which is in his diagram!) The BB pattern is not functional because there is no loop or other logic in the level 3 floor thus BB sets r4c2 and r6c8 are not rank 0.
10 Sets = {16R3 1C258 6C258 5N46}
15 Links = {1r159 3r5 6r158 4n2 1n5 6n8 6b1 1b3 136b5}
1 AUR = (16)r35c46
6 Eliminates = r4c45<>3, r5c278<>3, r6c5<>3
FM Combining ttt's AUR and Original Loop 1
If the AUR solution is combined with the original loop, several more eliminations appear including those in r4c2<>24 and 5 new digit 3 eliminations. The 5 new digit 3 eliminations occur because the AUR forces the entire level 3 floor to rank 0, as noted by the black cover-set highlights. There are now 13 eliminations.
13 Sets = {16R3 1C258 3C258 6C258 5N46}
17 Links = {1r159 3r259 6r158 4n2 1n5 6n8 6b1 1b3 136b5}
1 AUR = (16)r35c46
13 Eliminations = r2c14<>3, r4c2<>24, r4c45<>3, r5c278<>3, r6c5<>3, r9c467<>3
FM Loop 2, Additional Constraints
The AUR above uses 2 row base sets 16R3 as part of its strong inference. The original FM Loop-2 below uses 6 column bases sets and 6 row base sets that include 16R3 used by the AUR. This loop eliminates 24r4c2 and 6 additional candidates in levels 3 and 6. The extra eliminations occur because 4 extra cell link sets in r37c46 introduce new constraints that make levels 3 and 6 rank 0. These 4 cell sets are not used to cover the logic and are not considered cover sets.
14 Sets = {136R3 136R7 136C2 136C8 5N46}
21 Links = {136r5 136c4 136c6 4n2 37n4 37n6 6n8 1b37 3b19 6b19}
8 Eliminations = r1c3<>6, r2c1<>3, r4c2<>2, r4c2<>4, r5c3<>6, r5c7<>3, r8c9<>6, r9c7<>3
FM Full Loop Solution
What happens if the AUR is integrated with the FM Loop 2? The initial answer is nothing unless all of the Loop 1 base sets are added, which will cause 15 eliminations.
However, Loop 2 defines an inner rectangle whose corners are r37c46. This rectangle also encloses 4 possible AURs. When all 4 AUR are added to the Loop 2 logic the result now produces 32 eliminations all based on the original 14 base sets, and no further integration produces additional eliminations. This pretty much destroys FM .
14 Sets = {136R3 136R7 136C2 136C8 5N46}
27 Links = {1r5 3r456 6r456 136c4 136c6 4n2 6n8 1b37 3b14569 6b14569}
4 AURs = (13)r35c46 + (16)r35c46 + (13)r57c46 + (16)r57c46
32 Eliminations
Platinum Blond
Platinum Blond makes a good comparison because it is both different and difficult. It does not share the same symmetry as many other puzzles however, like Golden Nugget, it can be morphed to a more symmetric form. Platinum Blond is also short because it uses floors 678 making it very short in 3D images. Platinum Blond also has some surprises.
PB Initial Loop
An initial search on PB shows a loop similar to Golden Nugget with a pair of strong cell sets (BB pattern) in box 3. However, it has 3 weak cell sets that are all rank 0 and cause eliminations. This is perhaps a bi-tri. Once major difference is the pattern uses a digit 4 base set. This loop makes 6 eliminations.
12 Sets = {679R3 679R4 4679R7 12N7}
15 Links = {6c157 7c167 9c257 47n8 7n9 679b3}
6 Eliminations = r4c8<>234, r7c8<>231
PB Initial Loop Morph
Platinum Blond is morphed to a form similar to FM and 4 AURs are added to the same locations that were used in FM.
PB Full Solution, 36 Eliminations
A search discovers a solution of the same type as the FM full loop solution above, which uses all the same logical methods. This results in 36 eliminations.
18 Sets = {679R2 679R5 4679R8 679C3 679C7 46N5}
29 Links = {7r7 4c4 6c158 7c459 9c2458 28n4 8n6 4b8 6b357 7b14589 9b15689}
4 AURs = (67)r46c35 + (69)r46c35 + (67)r46c57 + (69)r46c57
36 Eliminations =
r2c4<>2, r2c4<>3, r2c4<>4, r2c4<>6, r2c5<>7, r2c5<>9, r3c1<>7, r3c5<>7,
r4c1<>7, r4c2<>9, r4c5<>6, r4c8<>9, r4c9<>7, r5c4<>7, r5c4<>9, r5c6<>7,
r5c6<>9, r6c1<>7, r6c2<>9, r6c4<>7, r6c4<>9, r6c5<>6, r6c8<>9, r6c9<>7,
r7c4<>7, r7c9<>7, r8c4<>2, r8c4<>3, r8c4<>6, r8c5<>7, r8c5<>9, r8c6<>1, r8c6<>6, r9c4<>9, r9c5<>9,r9c8<>9
PB What is This? 17 More Eliminations
However, the Platinum Blond story is not finished, as perhaps that of other monsters. The following 17 eliminations are from completely different logic, which is also not based on floors. It has some resemblance to and SK loop because it is rank 0 with equal numbers of base and cover sets however, it is geometrically different from an SK loop and cannot be morphed into one.
It is made of from hidden and naked AALS and one additional set.
1) A hidden row AALS (4 rows with digits in 6 columns) in row 1.
2) An AALS in row 3. (digits 123467)
3) An AALS in row 7 (digits 123678)
4) An AALS in row 9 (digits 12389)
5) A box set 8B9.
16 Sets = {1235R1 3N3467 7N3467 9N467 8B9}
16 Links = {467r3 678r7 89r9 1c67 2c47 3c34 1n19}
17 ELiminations = r1c9<>4, r2c4<>23, r3c15<>7, r3c2<>4, r3c58<>6,
r4c3<>3, r6c7<>12, r7c9<>7, r8c4<>23, r8c6<>1, r9c58<>9
Last edited by Allan Barker on Tue Jan 20, 2009 9:41 pm, edited 1 time in total.
- Allan Barker
- Posts: 266
- Joined: 20 February 2008
by Allan Barker » Sat Jan 17, 2009 2:25 am
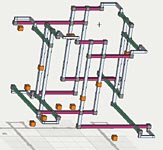
Relevant Diagrams
.
.
Last edited by Allan Barker on Fri Jan 16, 2009 10:31 pm, edited 1 time in total.
- Allan Barker
- Posts: 266
- Joined: 20 February 2008
by Allan Barker » Sat Jan 17, 2009 2:30 am
Thumbs to 3D Images
These are 3D images of above 2D grids.
Original SK Loop from Easter Monster
Fata Morgana Part 1
Fata Morgana Part 2
Platinum Blond
These are 3D images of above 2D grids.
Original SK Loop from Easter Monster
Fata Morgana Part 1
Fata Morgana Part 2
Platinum Blond
- Allan Barker
- Posts: 266
- Joined: 20 February 2008
by champagne » Sat Jan 17, 2009 4:20 am
Hi Alan,
Huge and impressive work.
I did not know you were so close to merging AUR logic with your base logic.
I will be very short in time next days to dig in that. I would just stress on tthree points after a quick reading.
1) I noticed that many eliminations based on AUR can be found in a bi-floors analysis. this can help the players. It is what I called the "double XWing"
2) Platinium Blond is not a full "bi bi", but not so far and has three elementary "bi bi" with one cell in common. You are far ahead of me, but as "ttt" solved it, I think it will be in due time an easy extension of the process.
3) For the players, a SLG for a full "bi bi" is very easy to build following these guidelines.
3.1 four cells 2 are Sets (the base of the "bi bi") 2 are linksets (the target of the "bi bi")
3.2 Other Sets are in the direction (row or column) of the base, linksets in the other direction. One box linkset is added for each digit in the box containing the base
3.3 Sets and linksets can be searched in each floor just looking for the minimum necessary to establish the "bi bi"elementary property.
I am convinced this is true but it must be checked. The underlying assumption is that the base is always in the same box.
The process can be achieve by a human. No need for a computer. Nevertheless, it is necessary to have the good nose and to smell where that animal can be. As "ttt" said, it can be easier for a computer than for a human to see it.
champagne
ps: the statistics made on the frequency of that pattern let think as you say that most "hardest puzzles" will be solved in a much easier way. As far as I could see, "bi bi" are not always as active as in Golden Nugget. it would be interesting to know what you find in Silver Plate which seems to resist more.... and some puzzle have none of the two patterns SK;BB
Huge and impressive work.
I did not know you were so close to merging AUR logic with your base logic.
I will be very short in time next days to dig in that. I would just stress on tthree points after a quick reading.
1) I noticed that many eliminations based on AUR can be found in a bi-floors analysis. this can help the players. It is what I called the "double XWing"
2) Platinium Blond is not a full "bi bi", but not so far and has three elementary "bi bi" with one cell in common. You are far ahead of me, but as "ttt" solved it, I think it will be in due time an easy extension of the process.
3) For the players, a SLG for a full "bi bi" is very easy to build following these guidelines.
3.1 four cells 2 are Sets (the base of the "bi bi") 2 are linksets (the target of the "bi bi")
3.2 Other Sets are in the direction (row or column) of the base, linksets in the other direction. One box linkset is added for each digit in the box containing the base
3.3 Sets and linksets can be searched in each floor just looking for the minimum necessary to establish the "bi bi"elementary property.
I am convinced this is true but it must be checked. The underlying assumption is that the base is always in the same box.
The process can be achieve by a human. No need for a computer. Nevertheless, it is necessary to have the good nose and to smell where that animal can be. As "ttt" said, it can be easier for a computer than for a human to see it.
champagne
ps: the statistics made on the frequency of that pattern let think as you say that most "hardest puzzles" will be solved in a much easier way. As far as I could see, "bi bi" are not always as active as in Golden Nugget. it would be interesting to know what you find in Silver Plate which seems to resist more.... and some puzzle have none of the two patterns SK;BB
- champagne
- 2017 Supporter
- Posts: 7455
- Joined: 02 August 2007
- Location: France Brittany
by Allan Barker » Tue Jan 20, 2009 10:56 pm
Symmetry Properties and Smart Logic
Many of the toughest puzzles share a degree of symmetry that results in large symmetrical structures. SK loops are large but logically simple and uniform. By contrast, structures like those of FM have distinct parts that operate to implement a specific global function.
The symmetry of such structures can lead to very simple solutions. Below are two FM style loops using the digits 159, for clarity. The first loop has 3 rotationally symmetric layers that are identical. The second loop is the same except that layer 1 is anti-symmetric from the others.
Note the first loop. Fully symmetrical structures cannot produce an asymmetrical solution. Thus, no solution can choose between the 3 sets of candidates in the two cell sets in r5c46 because these cells contain only two truths. In the case of this particular loop, there is no solution at all.
In the second loop, anti-symmetric layer 1 breaks the 3-way symmetry, which allows a solution. However, any solution must treat layers 5 and 9 exactly the same, and must therefore contain [59][59]. In other words, any solution based on this symmetry can only remove the digits [1][1]. As expected, this loop has a solution that removes both 1s (eliminations are in red). In the case of FM, this virtually solves the puzzle.
3 Symmetrical Layers
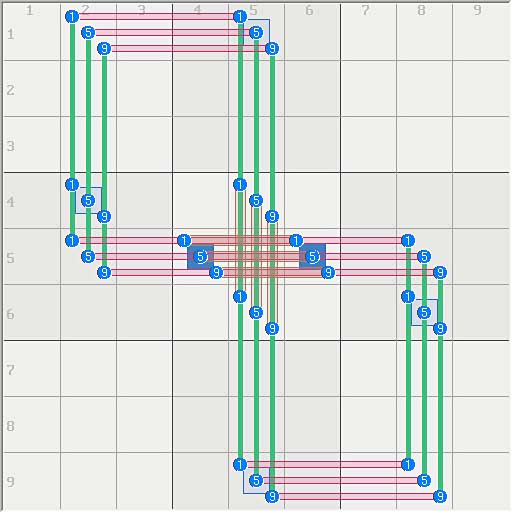
2 Symmetrical, 1 Anti-Symmetrical Layers
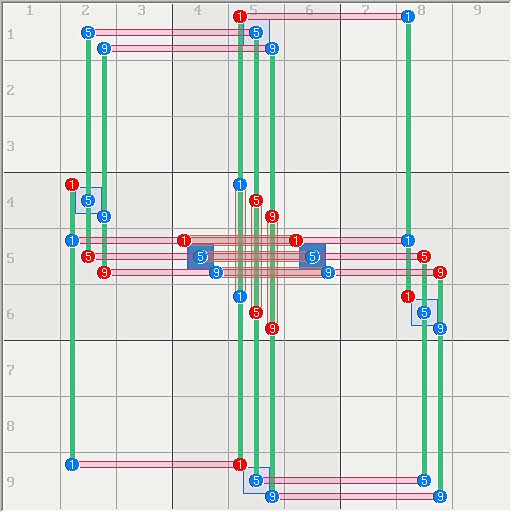
Silver Plate
Although puzzles like Silver Plate have 4 layers, one of the layers is incomplete thus there are still 2 identical layers. If the symmetrical solution is imposed on Silver Plate, (r6c5<>1, r6c56<>3) the loop produces the following eliminations and the puzzle collapses to a whimp.
The symmetry argument seems to work for 4 layer puzzles, so far there is no good proof that the solution must choose the 2 identical layers. Some more work needs to be done to define the conditions under which this is true.
Many of the toughest puzzles share a degree of symmetry that results in large symmetrical structures. SK loops are large but logically simple and uniform. By contrast, structures like those of FM have distinct parts that operate to implement a specific global function.
The symmetry of such structures can lead to very simple solutions. Below are two FM style loops using the digits 159, for clarity. The first loop has 3 rotationally symmetric layers that are identical. The second loop is the same except that layer 1 is anti-symmetric from the others.
Note the first loop. Fully symmetrical structures cannot produce an asymmetrical solution. Thus, no solution can choose between the 3 sets of candidates in the two cell sets in r5c46 because these cells contain only two truths. In the case of this particular loop, there is no solution at all.
In the second loop, anti-symmetric layer 1 breaks the 3-way symmetry, which allows a solution. However, any solution must treat layers 5 and 9 exactly the same, and must therefore contain [59][59]. In other words, any solution based on this symmetry can only remove the digits [1][1]. As expected, this loop has a solution that removes both 1s (eliminations are in red). In the case of FM, this virtually solves the puzzle.
3 Symmetrical Layers
2 Symmetrical, 1 Anti-Symmetrical Layers
Silver Plate
Although puzzles like Silver Plate have 4 layers, one of the layers is incomplete thus there are still 2 identical layers. If the symmetrical solution is imposed on Silver Plate, (r6c5<>1, r6c56<>3) the loop produces the following eliminations and the puzzle collapses to a whimp.
The symmetry argument seems to work for 4 layer puzzles, so far there is no good proof that the solution must choose the 2 identical layers. Some more work needs to be done to define the conditions under which this is true.
- Allan Barker
- Posts: 266
- Joined: 20 February 2008
by Allan Barker » Thu Jan 29, 2009 11:51 pm
Set Logic Diagrams and Recent BB Pattern Solutions
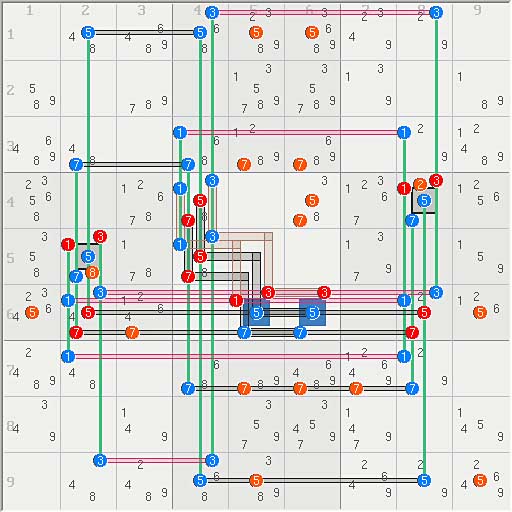
The following diagrams show some of the base/cover set solutions for 4 puzzles recently studied/solved using BB patterns here bi bi pattern in hardest puzzles and here AIC's net equivalent to forcing net. The puzzles include tarx0134, coly013, and coly510, and ducdiamond1. All puzzles are morphed to help show symmetry. These solutions show how much damage a pair of exocets can do to a puzzle. AUR logic and symmetry are not used. Tarx0134 and ducdiamond1 have a lot of variety (not all shown), including a stealth exocet?.( Tarx0134-B).
Solutions for Coly510 and ducdiamond1 are from RonK, who has been helping to test out a new set logic editor.Thanks, Ron.
Note 1: Base sets are solid colors, cover sets are shaded colors. Black shaded color indicates rank 0 cover sets. These often correspond to the second part of a BB pattern.
tarx0134
A) Tarx0134, Digits 3458, 18 base sets, 23 eliminations
B) Tarx0134, Digits 3458, 18 base sets, no primary BB pair, 31 eliminations
C) Tarx0134, Digits 3458, 18 base sets, row/column/box design, 31 eliminations
D) Tarx0134, Digits 348, 12 base sets, <extra digit 5 set>, 17 eliminations
Coly013
A) Coly013, Digits 1689, 16 base sets, 30 eliminations
B) Coly013, Digits 1689, 16 base sets, 46 eliminations, [extra cover sets]
Coly510
A) Coly510, Digits 1247, 16 base sets, 29 eliminations
B) Coly510, Digits 1247, 16 base sets, 40 eliminations [extra cover sets]
ducdiamond1
Example A is RonK's fully integrated SK loop and "core" loop. Example B shows the stand alone core that uses 4 row base sets from the SK loop.
A) ducdiamond1 , Digits 1267, 20 base sets, 31 eliminations [full solution, morphed]
B) ducdiamond1 , Digits 1267, 12 base sets, 10 eliminations [unmorphed]
C) ducdiamond1 , Digits 16[27, single bi-value set], 12 base sets, 4 eliminations [unmorphed]
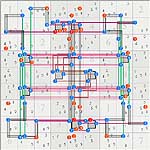
The following diagrams show some of the base/cover set solutions for 4 puzzles recently studied/solved using BB patterns here bi bi pattern in hardest puzzles and here AIC's net equivalent to forcing net. The puzzles include tarx0134, coly013, and coly510, and ducdiamond1. All puzzles are morphed to help show symmetry. These solutions show how much damage a pair of exocets can do to a puzzle. AUR logic and symmetry are not used. Tarx0134 and ducdiamond1 have a lot of variety (not all shown), including a stealth exocet?.( Tarx0134-B).
Solutions for Coly510 and ducdiamond1 are from RonK, who has been helping to test out a new set logic editor.Thanks, Ron.
Note 1: Base sets are solid colors, cover sets are shaded colors. Black shaded color indicates rank 0 cover sets. These often correspond to the second part of a BB pattern.
tarx0134
- Code: Select all
+-----------------------------------------------------------------------------------------------+
| 1-567-8 7(58) 3 | 19(58) 167-89 67(58) | 2 19(5) 4 |
| 1578 9 17(4) | 2 178(3-4) -7(34-58) | 157 6 17(3) |
| 12-567 27(45) 12-467 | 19(345) 1-3-4679 67(345) | 8 19(35) 1-379 |
+-----------------------------------------------------------------------------------------------+
| 12358 -2(3458) 12-4 | 7 348 9 | 1-456 -1(3458) 1368 |
| 19(38) 6 19(4) | (3-48) 5 2 | 19(4) 7 19(38) |
| 35789 -7(3458) -479 | 6 348 1 | -459 -9(3458) 2 |
+-----------------------------------------------------------------------------------------------+
| 2-3679 27(3) 8 | 19(34) 12-3-4679 67(3-4) | 1-4679 19(4) 5 |
| 3679 1 679 | -9(3458) 3679(-48) -6-7(3458) | 679(4) 2 679(8) |
| 4 27 5 | 19(8) 1267-89 67(8) | 3 19(8) 167-89 |
+-----------------------------------------------------------------------------------------------+
A) Tarx0134, Digits 3458, 18 base sets, 23 eliminations
B) Tarx0134, Digits 3458, 18 base sets, no primary BB pair, 31 eliminations
C) Tarx0134, Digits 3458, 18 base sets, row/column/box design, 31 eliminations
D) Tarx0134, Digits 348, 12 base sets, <extra digit 5 set>, 17 eliminations
Coly013
- Code: Select all
+--------------------------------------------------------------------------------------+
| 3-67 3678 34-67 | (168) 12468 5 | 9 12678 -1247-8 |
| 5-67-9 6789 1 | (689) 24689 3 | 2457-8 2678 247-8 |
| 5(69) 2 45(6) | 7 -4(1689) 4(-1-6-8-9) | 45(8) 3 4(18) |
+--------------------------------------------------------------------------------------+
| 234-67 367 9 | 3568 3468 2468 | 1 278 2357-8 |
| 23(16) 5 23(6) | -3(1689) 7 -2(1689) | 23(8) 4 23(89) |
| -12347 137 8 | 1359 1349 1249 | 6 279 2357-9 |
+--------------------------------------------------------------------------------------+
| 23(169) 4 23(6) | 3(-1-6-8-9) -3(1689) 7 | 23(8) 5 23(189) |
| -12357-9 1379 2357 | 4 13589 (189) | 237-8 12789 6 |
| 8 13679 35-67 | 2 13569 (169) | 347 179 -1347-9 |
+--------------------------------------------------------------------------------------+
A) Coly013, Digits 1689, 16 base sets, 30 eliminations
B) Coly013, Digits 1689, 16 base sets, 46 eliminations, [extra cover sets]
Coly510
- Code: Select all
+-----------------------------------------------------------------------------------------------+
| -2569 -1569 125 | (127) 12367 8 | 12357 4 356-7 |
| 7 -1-4568 12458 | (124) 12346 9 | 1235 -1-23568 3568 |
| 68(24) 68(14) 3 | 5 -6(1247) 6(-1-2-4-7) | 9 -6-8(127) 68(7) |
+-----------------------------------------------------------------------------------------------+
| 3-4589 3-4589 4578 | 24789 -23-46-789 23467 | 2357 -2356-79 1 |
| 39(4) 39(14) 6 | -9(1247) 5 -3(1247) | 8 -3-9(27) 39(7) |
| 3589 2 1578 | 1789 -136-789 1367 | 357 356-79 4 |
+-----------------------------------------------------------------------------------------------+
| 38(24) 38(4) 9 | 8(-1-2-4-7) -8(1247) 5 | 6 -3-8(17) 38(7) |
| 1 -4568 458 | 3 4789 (47) | 457 5-789 2 |
| -23-458 7 2458 | 6 12489 (124) | 1345 -13589 3589 |
+-----------------------------------------------------------------------------------------------+
A) Coly510, Digits 1247, 16 base sets, 29 eliminations
B) Coly510, Digits 1247, 16 base sets, 40 eliminations [extra cover sets]
ducdiamond1
Example A is RonK's fully integrated SK loop and "core" loop. Example B shows the stand alone core that uses 4 row base sets from the SK loop.
A) ducdiamond1 , Digits 1267, 20 base sets, 31 eliminations [full solution, morphed]
- Code: Select all
+--------------------------------------------------------------------------------------+
| 1 49(67) 45-689 | 6789 5-6-789 3567 | 34-789 38(7) 2 |
| 89(7) 3 89(6) | -8-9(126-7) -8-9(126-7) 4 | 89(7) 5 89(1) |
| 45-789 49(7) 2 | 1789 -15-789 1357 | 6 38(17) -13489 |
+--------------------------------------------------------------------------------------+
| 23479 -4-9(1267) 13469 | 5 (1267) 8 | 2347 -3(1267) 1346 |
| 2457 8 1456 | (1267) 3 (1267) | 2457 9 1456 |
| 2357 (1267) 1356 | 4 (1267) 9 | 23578 -3-8(1267) 13568 |
+--------------------------------------------------------------------------------------+
| -23489 49(2) 7 | 2689 -245-689 256 | 1 38(26) 35-689 |
| 89(2) 5 89(1) | 3 -8-9(1-267) (1-267) | 89(2) 4 89(6) |
| 6 49(12) -13489 | 1289 -1-24589 125 | -23589 38(2) 7 |
+--------------------------------------------------------------------------------------+
B) ducdiamond1 , Digits 1267, 12 base sets, 10 eliminations [unmorphed]
C) ducdiamond1 , Digits 16[27, single bi-value set], 12 base sets, 4 eliminations [unmorphed]
- Code: Select all
+--------------------------------------------------------------------------------------+
| 1 45689 4679 | 3567 56-789 6789 | 378 34789 2 |
| 45789 2 479 | 1357 15-789 1789 | 1378 6 13489 |
| 789 89(6) 3 | 4 -789(126) -7-8-9(126) | 5 789 89(1) |
+--------------------------------------------------------------------------------------+
| 23479 13469 124679 | 8 (1267) 5 | 12367 2347 1346 |
| 2457 45(16) 8 | (1267) 3 (1267) | 9 2457 45(16) |
| 2357 1356 1267 | 9 (1267) 4 | 123678 23578 13568 |
+--------------------------------------------------------------------------------------+
| 289 89(1) 5 | -2(167) -289(167) 3 | 4 289 89(6) |
| 23489 7 249 | 256 -245689 2689 | 2368 1 35689 |
| 6 13489 1249 | 125 1-24589 1289 | 238 23589 7 |
+--------------------------------------------------------------------------------------+
- Allan Barker
- Posts: 266
- Joined: 20 February 2008
by champagne » Fri Jan 30, 2009 11:08 pm
Hi Allan,
Not that much time to spread the free time on to many topics, but if you need some interestng puzzles to study, I am for the time being weighing a 1500 puzzles lot from coloin with several where Exocets are true killers (unchecked). If you want to increase your sample file, I can, with the authorization of coloin, share some of them with you. I can also give you several where no exocet seem to work properly.
All these puzzles have the requirements to enter the group of top hardest without exocets.
champagne
Not that much time to spread the free time on to many topics, but if you need some interestng puzzles to study, I am for the time being weighing a 1500 puzzles lot from coloin with several where Exocets are true killers (unchecked). If you want to increase your sample file, I can, with the authorization of coloin, share some of them with you. I can also give you several where no exocet seem to work properly.
All these puzzles have the requirements to enter the group of top hardest without exocets.
champagne
- champagne
- 2017 Supporter
- Posts: 7455
- Joined: 02 August 2007
- Location: France Brittany
by Allan Barker » Sat Jan 31, 2009 1:42 am
champagne wrote:Hi Allan,
If you want to increase your sample file, I can, with the authorization of coloin, share some of them with you. I can also give you several where no exocet seem to work properly.
champagne
Hi Champage,
I would love to see them. Please make sure to include to strangest.
Allan
- Allan Barker
- Posts: 266
- Joined: 20 February 2008
by champagne » Sat Jan 31, 2009 3:44 pm
Hi Allan,
I am not sure I have identified the "strangest", but I can feed you (thanks to coloin) with various examples:
2 puzzles from a previous lot
#y707 is a puzzle the former version could not solve. It is solved without exocets using your model. It becomes nearly human with 2 exocets
It deteriorates with the new one and I did not have time to dig in it. Again 2 exocets and a significant fall.
This is a lot whith the small exocet, starting fom a bi value cell. I did not even had a look at them but the results are very surprising.
cola199 is a mixture of a smal exocet and a 1234 1234 pattern. "??" means I faced a problem to fix.
Just one more example of a 123 123 pattern. It seem that for such pattern, exocet gives always good results;
2 puzzles to investigate, no Exocet, but likely (at least in the second one) some fying fishes effects.
And a final lot with one or 2 Exocets. I gave examples as in 093 of puzzles where the solver finds an exocet with an AC of more than 2 cells.
In that lot, some exocets are efficient, some are not.
Should be noticed also that the scan comes after "easy" moves have been done. May be this explain the 3 exocets found in a259.
Last point, there are similarities in patterns. This likely comes from the process applied to create these puzzles.
I am not sure I have identified the "strangest", but I can feed you (thanks to coloin) with various examples:
2 puzzles from a previous lot
#y707 is a puzzle the former version could not solve. It is solved without exocets using your model. It becomes nearly human with 2 exocets
- Code: Select all
.1......87..4....9..3.9.5....9.6...5.....23..1.....6....6.8..5....2......4.7..... #coly707 63.1 217K BBr12c7 r4c8 r7c9 BBr56c9 r3c8 r7c7 12.7 print 51K
It deteriorates with the new one and I did not have time to dig in it. Again 2 exocets and a significant fall.
- Code: Select all
.1...2..8.4......9..3.8.5....8.6...5...7..3..4.....6....6.9..5.2....1........7... #coly885 85.0 325K BBr12c r4c8 r7c9 BB56c9 r3c8 r7c7 10.1 print 34K
This is a lot whith the small exocet, starting fom a bi value cell. I did not even had a look at them but the results are very surprising.
cola199 is a mixture of a smal exocet and a 1234 1234 pattern. "??" means I faced a problem to fix.
- Code: Select all
3.........9.4...6...7.3...5.2..48..........2.6.92.......5...1.7.6.9...8......1... #cola091 (50.2) 54.1 496K 1BB<< r4c3 r5c4 r6c8 6.6 105K
.....1..87.......9..3.9.5....9.6...5.7...23..1..4..6....6.3..5..........2....4... #cola095 (16.6) 10.1 136K 1BB<< r5c9 r3c8 r7c7 1BB<< r6c9 r3c8 r7c7 1.7 32K
........6..3.8..9..4.....85..5.9...8.7...2...1..4.......6.3...92....73.....1..... #cola199 (33.0) 14.0 243K 1BB<< r8c9 r2c7 r4c8 BBr89c9 r2c7 r4c8 ???
.....2..67..1....9..3.9.5....8.6...5.....43.....2..8....6.8..5.4.........7...1... #cola317 (79.7) 17.0 151K 1BB<< r2c7 r4c8 r7c9 4.7 69K
.....4..67..1....9..3.9.5....8.3...5...2..3.....4..8....9.8..5.2....1....7....... #cola351 (56.5) 48.0 466K 1BB<< r2c7 r4c8 r7c9 5.5 110K
7.......84.......9..3.9.5....8.6...5...1..3...2...46....9.8..5.2....1....7....... #cola646 (68.7) 65.5 668K 1BB<< r6c9 r3c8 r7c7 4.4 96K
Just one more example of a 123 123 pattern. It seem that for such pattern, exocet gives always good results;
- Code: Select all
5......8......5.63..3.8.9....8.5...9...2.....1....4.....9.6..3.2.........4.1..7.. #cola010 (50.8) 35.3 432K 3BBr12c7 r4c8 r7c9 5.8 154K
2 puzzles to investigate, no Exocet, but likely (at least in the second one) some fying fishes effects.
- Code: Select all
1.....5...8.6...2...3.....7.9.86........49.8.......2.......73...2.9.....5.7.....1 #cola036 (44.8)21.4 441K 34.9 256K
..1...5...8.2...6.3.......7.6.92........4..9.......8.6.....51...4.6.....5.7.....3 #cola607 (60.8)32.0 398K 38.0 229K
And a final lot with one or 2 Exocets. I gave examples as in 093 of puzzles where the solver finds an exocet with an AC of more than 2 cells.
In that lot, some exocets are efficient, some are not.
Should be noticed also that the scan comes after "easy" moves have been done. May be this explain the 3 exocets found in a259.
Last point, there are similarities in patterns. This likely comes from the process applied to create these puzzles.
- Code: Select all
.1......67.......9..6.9.5....8.3...5.....23.....4..8....3.8..5..7...1....2...4... #cola076 (26.6) 13.4 180K BBr12c7 r4c8 r7c9 BBr56c9 r3c8 r7c7 15.1 113K
.2.....83.......95..8.5......6.3...9.7...2...1..4.......9.6..3....7.....4....16.. #cola093 (30.1) 15.2 260K BBr3c1246 r4c8 r7c9 BBr12c7 r4c8 r7c9 21.5 170K
...7....3.......85..3.5..9...5.8...9.7...2...1..4.......9.6..3.4....1....2....6.. #cola117 (34.3) 13.9 243K BBr12c7 r4c8 r7c9 17.6 151K
.2......8...4....3..3.9.5....8.6...51.....9...7....6....6.8..5.7....1...2....4... #cola239 (43.9) 46.9 315K BBr12c7 r4c8 r7c9 BBr56c9 r3c8 r7c7 8.7 33K
.....7..3.......89..6.9..5...9.3...6.7...2...1..4.......5.8..9..2.1.....4.....6.. #cola259 (26.3) 11.6 240K BBr3c1246 r4c8 r7c9 BBr12c7 r4c8 r7c9 BBr5689c9 r3c7 r4c8 26.6 208K
.1......67.......9..3.9.5....8.6...52.....3.......48....9.3..5..7...1....2.4..... #cola268 (56.9) 46.1 320K BBr12c7 r4c8 r7c9 BBr56c9 r3c8 r7c7 8.7 33K
........5.8.4...9.3.....7...2..48..........2.6.92.........7.1...6.8...4...5..1..3 #cola548 (11.2) 13.0 144K BBr4c13 r5c4 r6c8 BBr6c56 r4c8 r5c2 14.8 138K
- champagne
- 2017 Supporter
- Posts: 7455
- Joined: 02 August 2007
- Location: France Brittany
by ronk » Sun Feb 01, 2009 12:05 am
champagne wrote:Last point, there are similarities in patterns. This likely comes from the process applied to create these puzzles.
Yes, I see several coly510-like puzzles in that set. coly707, for example, has exactly the same pattern as coly510.
Several of the solving methods for these monsters are based on symmetry, and several of us will be tempted to morph the puzzle to visualize this symmetry. Therefore, I've used gsf's solver to obtain a "best symmetry" for all 18 of coloin's puzzles that you've posted. Hopefully then, we can all be posting the same morph.
#!sudoku -c1,morph,msym,osym,orig,name,t1,t2,size,other
........2..9.8.6...4.2.7.....5....63....5....89....5...7.....1...3.6.9..1....4...,p-4,d-10,.1......87..4....9..3.9.5....9.6...5.....23..1.....6....6.8..5....2......4.7.....,coly707,63.1,,217K,BBr12c7 r4c8 r7c9 BBr56c9 r3c8 r7c7 12.7 print 51K
........7..8.9.6...2.7.1.....5....63....5....98....5.......2.4...3.6.8..41.......,p-2,p-11,.1...2..8.4......9..3.8.5....8.6...5...7..3..4.....6....6.9..5.2....1........7...,coly885,85,,325K,BBr12c r4c8 r7c9 BB56c9 r3c8 r7c7 10.1 print 34K
........3..3..57...4..6..9..2....9.6....2....8.4....2..9..8..6....1.75..1........,p-2,h-10,3.........9.4...6...7.3...5.2..48..........2.6.92.......5...1.7.6.9...8......1...,cola091,50.2,54.1,496K,1BB<< r4c3 r5c4 r6c8 6.6 105K
........7..7..21...3..6..9..5....6.3....5....8.9....5..9..3..6.......4..1....4..2,p-4,a-10,.....1..87.......9..3.9.5....9.6...5.7...23..1..4..6....6.3..5..........2....4...,cola095,16.6,10.1,136K,1BB<< r5c9 r3c8 r7c7 1BB<< r6c9 r3c8 r7c7 1.7 32K
........1.6...9.3...2.3.7..4..8.5........6....3.9...8...1.....4.5...8.9.7.....2..,d-3,a-11,........6..3.8..9..4.....85..5.9...8.7...2...1..4.......6.3...92....73.....1.....,cola199,33,14,243K,1BB<< r8c9 r2c7 r4c8 BBr89c9 r2c7 r4c8 ???
.....7......4....7..8.6.3....5....69....5....38....5....6.8.9..4....1.2..2......1,p-4,a-9,.....2..67..1....9..3.9.5....8.6...5.....43.....2..8....6.8..5.4.........7...1...,cola317,79.7,17,151K,1BB<< r2c7 r4c8 r7c9 4.7 69K
.....7......2....7..8.9.3....5....69....5....38....5....3.8.9..24......1...1...4.,p-4,p-11,.....4..67..1....9..3.9.5....8.3...5...2..3.....4..8....9.8..5.2....1....7.......,cola351,56.5,48,466K,1BB<< r2c7 r4c8 r7c9 5.5 110K
........1.....1.4...9.8.6....5....63....5....89....5....3.9.8.....7...2.74...2...,p-4,d-10,7.......84.......9..3.9.5....8.6...5...1..3...2...46....9.8..5.2....1....7.......,cola646,68.7,65.5,668K,1BB<< r6c9 r3c8 r7c7 4.4 96K
........2..1...4...8...9.5....6.35...3..9..8...58......9.3...6...2......4...7...1,p-4,d-8,5......8......5.63..3.8.9....8.5...9...2.....1....4.....9.6..3.2.........4.1..7..,cola010,50.8,35.3,432K,3BBr12c7 r4c8 r7c9 5.8 154K
........2.68..9...94.....8.....1...5...3..7....6..8.2....75.1....9..2...7.......3,d-5,d-6,1.....5...8.6...2...3.....7.9.86........49.8.......2.......73...2.9.....5.7.....1,cola036,44.8,21.4,441K,34.9 256K
........5..9..2.6..42..........1.7.....3..5....6..8.4.8...5...1.9...6...6..7..3..,d-5,d-6,..1...5...8.2...6.3.......7.6.92........4..9.......8.6.....51...4.6.....5.7.....3,cola607,60.8,32,398K,38 229K
........7...7.2.1...8.3.6....5....69....5....83....5....3.8.9...2.1.4...4........,p,d-12,.1......67.......9..6.9.5....8.3...5.....23.....4..8....3.8..5..7...1....2...4...,cola076,26.6,13.4,180K,BBr12c7 r4c8 r7c9 BBr56c9 r3c8 r7c7 15.1 113K
........7..9..3.6.4...6.1.....5.9.....8....5..2.3.8.....69...3..7....2..1.......4,d-4,a-12,.2.....83.......95..8.5......6.3...9.7...2...1..4.......9.6..3....7.....4....16..,cola093,30.1,15.2,260K,BBr3c1246 r4c8 r7c9 BBr12c7 r4c8 r7c9 21.5 170K
........6.89....3.35...9.......7...2...1..4....3..5.9.....2.1....5..8.6.7..4.....,d-3,h-13,...7....3.......85..3.5..9...5.8...9.7...2...1..4.......9.6..3.4....1....2....6..,cola117,34.3,13.9,243K,BBr12c7 r4c8 r7c9 17.6 151K
........4...1.4.....6.8.9....5....83....5....69....5....8.6.3...1.7.2...7......2.,p-2,p-9,.2......8...4....3..3.9.5....8.6...51.....9...7....6....6.8..5.7....1...2....4...,cola239,43.9,46.9,315K,BBr12c7 r4c8 r7c9 BBr56c9 r3c8 r7c7 8.7 33K
........6.85....9.39...6.......1...4...7..2....6..9.5.....4.1....9..3.8.7..2.....,d-3,a-11,.....7..3.......89..6.9..5...9.3...6.7...2...1..4.......5.8..9..2.1.....4.....6..,cola259,26.3,11.6,240K,BBr3c1246 r4c8 r7c9 BBr12c7 r4c8 r7c9 BB r5689c9 r3c7 r4c8 26.6 208K
.....4......1....4..9.3.6....5....38....5....96....5....3.9.8..7......2..1.7.2...,p-4,d-9,.1......67.......9..3.9.5....8.6...52.....3.......48....9.3..5..7...1....2.4.....,cola268,56.9,46.1,320K,BBr12c7 r4c8 r7c9 BBr56c9 r3c8 r7c7 8.7 33K
.....5......7....3..4.9.8....2....96....2....84....2....8.4.6..1....3.5..7.1.....,p-2,h-10,........5.8.4...9.3.....7...2..48..........2.6.92.........7.1...6.8...4...5..1..3,cola548,11.2,13,144K,BBr4c13 r5c4 r6c8 BBr6c56 r4c8 r5c2 14.8 138K
The file is compatible with Excel's csv format and gsf's solver. The first five data fields are ...
1) the morphed "best symmetric" puzzle
2) a measure of symmetry for the morph
3) a measure of symmetry for the original
4) the original puzzle, and
5) the puzzle name
champagne, I've retained all your data and columnized it (in Excel) as best I could.
[edit: corrected data errors]
- ronk
- 2012 Supporter
- Posts: 4764
- Joined: 02 November 2005
- Location: Southeastern USA
by Allan Barker » Wed Feb 04, 2009 1:52 am
Cola036 - Private Morph
Hi Champagne,
I took a look at Cola036 and found the following 4 layer loop that eliminates 26 candidates, 29 with a few more cover sets. It is obviously related to the same kind of patterns as in other puzzles. The major difference seems to be the requirment for 3 strong cell sets in the center box. Similar to other monster loops, it has two symmetric layers, a 90 degree rotationally symmetric layer, and a slightly distorted layer.
The morph that makes the logic symetrical (at least for this puzzle) is very different from the morph in the list of gsf's best symmetry morphs, above.
Thumbs
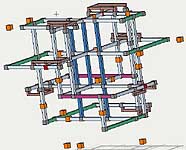
Hi Champagne,
I took a look at Cola036 and found the following 4 layer loop that eliminates 26 candidates, 29 with a few more cover sets. It is obviously related to the same kind of patterns as in other puzzles. The major difference seems to be the requirment for 3 strong cell sets in the center box. Similar to other monster loops, it has two symmetric layers, a 90 degree rotationally symmetric layer, and a slightly distorted layer.
Ronk wrote:Several of the solving methods for these monsters are based on symmetry, and several of us will be tempted to morph the puzzle to visualize this symmetry. Therefore, I've used gsf's solver to obtain a "best symmetry" for all 18 of coloin's puzzles that you've posted. Hopefully then, we can all be posting the same morph.
The morph that makes the logic symetrical (at least for this puzzle) is very different from the morph in the list of gsf's best symmetry morphs, above.
- Code: Select all
cola036,44.8,21.4,441K,34.9 256K
1.....5...8.6...2...3.....7.9.86........49.8.......2.......73...2.9.....5.7.....1 --original--
........2.68..9...94.....8.....1...5...3..7....6..8.2....75.1....9..2...7.......3 --best symmetry--
..1...5...8.6...2.3.......7.9.8.6.........2......94.8.....7.3.2.2.9.....7.5.....1 --this one--
+--------------------------------------------------------------------------------------------------------+
| 2469 46(7) 1 | 24(37) 248(-3) 289(37) | 5 469(3) -34689 |
| 49(5) 8 479 | 6 -4(135) -9(1357) | 149 2 349 |
| 3 456 2469 | 245(1) 24-58(-1) 2589(1) | -14689 469(1) 7 |
+--------------------------------------------------------------------------------------------------------+
| 124(5) 9 2347 | 8 -12-3-5 6 | 147 -4(1357) 34(5) |
| -1468(-5) 46(1357) -346-78 | (1357) (135) (1357) | 2 469(1357) -3469(-5) |
| 126(5) -6(1357) 2367 | 12357 9 4 | 167 8 36(5) |
+--------------------------------------------------------------------------------------------------------+
| -14689 46(1) 4689 | 45(1) 7 58(1) | 3 456 2 |
| 1468 2 3468 | 9 -4-6-8(135) -8(135) | 4678 -4-6(57) 468(5) |
| 7 46(3) 5 | 24(3) 2468(-3) 28(3) | 4689 469 1 |
+--------------------------------------------------------------------------------------------------------+
Thumbs
- Allan Barker
- Posts: 266
- Joined: 20 February 2008
by ronk » Wed Feb 04, 2009 10:21 am
That's a very nice result for cola036. I worked on it for some time and found nothing. Actually, I found one elimination only to later discover there was a hidden single in that cell.
Different goals. For two morphs with equal distances from perfect symmetry, gsf's algorithm chooses the morph with the lowest row-order minimum lexicographical order of the clues, where all clues are considered to be of equal value. Therefore, I think the greater the distance from perfect symmetry, the less likely it will produce the logical symmetry we want.
Particularly disruptive are rows or columns with zero or one clue(s). However, even in those cases gsf's best symmetry result can still be helpful. For example, for the cola036 puzzle of your example, the best symmetry is d-5. You could have retained d-5 symmetry and still had reasonable logical symmetry with a single (r1,r4)(c1,c4) morph.
In any case, gsf's distance result, "d-5" for this example, provides a goal to maintain during manual morphing.
Allan Barker wrote:The morph that makes the logic symetrical (at least for this puzzle) is very different from the morph in the list of gsf's best symmetry morphs, above.
Different goals. For two morphs with equal distances from perfect symmetry, gsf's algorithm chooses the morph with the lowest row-order minimum lexicographical order of the clues, where all clues are considered to be of equal value. Therefore, I think the greater the distance from perfect symmetry, the less likely it will produce the logical symmetry we want.
Particularly disruptive are rows or columns with zero or one clue(s). However, even in those cases gsf's best symmetry result can still be helpful. For example, for the cola036 puzzle of your example, the best symmetry is d-5. You could have retained d-5 symmetry and still had reasonable logical symmetry with a single (r1,r4)(c1,c4) morph.
- Code: Select all
. 1 . | . . . | . . *5
3 . . | . . . | 7 . .
. . 8 | . . *6 | . 2 .
----------+-----------+----------
. . . | . . . | . . 2
. . *9 | . 6 8 | . . .
. . . | *9 4 . | . 8 .
----------+-----------+----------
*7 5 . | . . . | 1 . .
. . 2 | . . 9 | . . .
. . . | 7 . . | . . 3
'*' marks the 5 clue distance from perfect diagonal symmetry
In any case, gsf's distance result, "d-5" for this example, provides a goal to maintain during manual morphing.
- ronk
- 2012 Supporter
- Posts: 4764
- Joined: 02 November 2005
- Location: Southeastern USA
by champagne » Wed Feb 04, 2009 3:53 pm
Allan Barker wrote:Cola036 - Private Morph
Hi Champagne,
I took a look at Cola036 and found the following 4 layer loop that eliminates 26 candidates, 29 with a few more cover sets. It is obviously related to the same kind of patterns as in other puzzles. The major difference seems to be the requirment for 3 strong cell sets in the center box. Similar to other monster loops, it has two symmetric layers, a 90 degree rotationally symmetric layer, and a slightly distorted layer.
Hi Allan,
With a base of three cells this is quite different. t would be easier to studyit with your usual list of set, linksets, eliminations.
champagne
- champagne
- 2017 Supporter
- Posts: 7455
- Joined: 02 August 2007
- Location: France Brittany
22 posts
• Page 1 of 2 • 1, 2
