The New Sudoku Players' Forum

by **Mauriès Robert** » Tue Dec 03, 2019 8:23 am

Hi Champagne and SpAce,
I am not familiar with this notion of MSLS, so I have trouble following your discussions.
Where can we find the definition of an MSLS and the demonstration of the eliminations that the MSLS produces?
Thank you to you.
Robert

by **SpAce** » Tue Dec 03, 2019 9:50 am

Hi eleven,

eleven wrote:Thanks for those 5 lines, SpAce. I never bothered to read about MSLS, because i thought, it is useless to search for one manually. So i did not understand the (your) notation too. But looking at this for 15 minutes made it clear.

Glad to hear that! I also avoided MSLS for a long time because David's explanations made my head ache. The spotting procedure seemed simple enough, but the weird balance calculations and elimination checks and pretty much everything else were lost on me (and still are). I simply refuse to use techniques that I don't understand even if they're demonstrably effective, so I never bothered with it until now. For me the key was to see it through the normal set logic POV which David tried to desperately avoid.

And yes, it could be found manually - though i would have to be very bored to try it.

It actually seems very easy, at least with the simple examples where the two complementary groups of digits can be quickly identified and the Rank 0 balance is found without any adjustments. The potential for such patterns is also easy to see if you just look at the givens (and solved cells if any). If two groups of them (4+5 digits, covering all nine) form two imaginary rectangle-patterns with little overlap in either rows or columns, you probably have an MSLS. Or so it seems with my minimal sample size so far. For example, let's look at David's original Shark puzzle (another one of yours, it seems):

David P Bird wrote:.......89.5.1.....6....31...7...16......9..2...8.....4..4.2....7..5..3...6...7... 3329 eleven 991 11.20 1.20 1.20 713 B4B

To identify the two groups of digits and any misfits I colored the solved cells:

digit groups: Show

Then I completed their rectangles:

rectangles: Show

So, we have the blue group with (2489) and the beige group with (13567), as well as the cyan 6r5c3 which is inside the wrong rectangle (we'll just ignore it for now, hoping it won't cause trouble). By David's conventions, those two digit groups would be called Home and Away based on the number of digits (Home: 4, Away: 5), but it's totally arbitrary because they have no designated roles. In set logic terms, one will be used for row links and the other for column links, if we're looking for a naked MSLS with cell truths as usual, but they can be either way. They can also be used as row truths or column truths in a hidden MSLS or a multi-fish, but that's a bit more complicated scenario (see examples below). (Just in case, "truth" is Allan Barker's synonym for a base set, and "link" for a cover set).

In some situations there's only one easy way the Home and Away digit groups can be assigned for rows and columns (like in the previous 16x16 example I couldn't make it work with the Home in rows). Here it doesn't matter at all. I guess one way to see that is that the intersection cells, which become the naked truths, are unoccupied both ways. Again coloring helps (me):

intersections: Show

The dark green highlights the Home-rows + Away-columns intersections, and the light green vice versa. We can see that they form two non-overlapping rectangles, one 5x4 and the other 4x5 in this case, and neither contains any solved cells. Depending on our choice, one or the other will contain the 20 cell truths that feed our row and column links. Either way no eliminations occur in those cells. Eliminations can only happen within the empty cells of the Home (blue) and Away (beige) rectangles and either can only eliminate candidates from its own digit group. The eliminations are the same regardless of which of the two naked MSLSs is used (if both are usable), and at least in this case they're the same for any other Rank 0 pattern I've found based on those two digit groups as well.

So, let's assume we assign the Home to the rows and the Away to the columns. Thus the dark green intersections become the cell truths whose candidates need to be covered by the Home-rows (blue) and Away-columns (beige):

MSNS 1: Show

As said, the truths are the 20 intersection cells of the Home-rows and Away-columns (r1567c12467 for the N-allergic). All of their candidates are covered by the row and column links; rows covering the (still unsolved) Home-digits and columns covering the (still unsolved) Away-digits, so none in the intersection cells is left uncovered (because together the links cover all nine digits and the intersections are hit by both). Since the number of truths and links is the same (20) we have Rank 0 without any need for balancing, and all covered non-base candidates can be eliminated as in any Rank 0 situation. Looks like the misfit cyan 6r5c3 didn't bother us after all. (It will, very slightly, with the hidden variants and multi-fishes below.)

The other way (Home-columns, Away-rows), i.e. light green cell truths, works just as well in this case:

MSNS 2: Show

Those were both naked MSLS, i.e. using cell truths. What about the hidden variant which uses rows and columns as truths and cells as links? We can produce those too using the same digit groups and rows and columns, if we flip them around:

MSHS 1: Show

MSHS 2: Show

Obviously those pure hidden locked sets with all cell links didn't make much sense in this case, and I'm not sure they ever do with these large MSLS patterns. However, we can also use just one of the digit groups for both truths and links (one role in rows and the other in columns, or possibly a mix) to get much more efficient patterns with house truths. If I've now understood things correctly, those would be examples of the elusive Multi-Fishes. A couple of them:

MF 1: Show

MF 2: Show

MF 3: Show

MF 4: Show

Those are all hand-crafted, so I can't guarantee they're flawless. Can anyone find other variants, perhaps multi-fish with mixed rows and columns? Box sets?

[Added:] This base/cover, home/away thingie only confused me. If you have 16 digits in 16 cells, you can eliminate them outside in the units, wherever one is restricted.

Of course. Isn't that the definition of a multi-sector naked set, so the name fits? It just sounds a bit weird if stated like that because we only have 9 distinct digits, after all

Whatever it's called, it boils down to 16 cells with 16 digit covers, which is a straight-forward base\cover Rank 0 situation. For me it's the simplest way to look at it anyway. If you have another way to see it, like you apparently do with the simpler DDS situations (where there's only one cover sector for each digit, thus max 9 sectors), that's great. In reality, that's a base\cover problem too.

So what is this distinction for ?

Well, no matter how you see it and what you call it, I just think it gets much harder with larger patterns and multiple covers per digit. Or can you spot the 16 or 20 cells whose candidates can be covered with exactly as many houses just by looking at the pm? I surely can't. Even if I know the cells, I need to color and write down the covers to be sure the counts match and nothing is missed. Can you do that otherwise?

The bigger problem is spotting those cells anyway, and that's where David's method of identifying those two groups of digits really helps. With that it's relatively easy to spot the potential for such large-scale Rank 0 patterns and then find the truths and links for them. I think that's the real piece of gold in David's method, and everything else is there just to confuse people

At least I don't see much need for his complicated counting methods, which I still don't even understand (and probably won't care to learn). For me, after spotting the pattern potential, it becomes a normal set logic problem of finding a Rank 0 balance between truths and links, and I don't see anything in David's methods that would simplify that (or make it anything else, really).

by **SpAce** » Tue Dec 03, 2019 10:53 am

Hi Robert,

Mauriès Robert wrote:I am not familiar with this notion of MSLS, so I have trouble following your discussions.

May I ask what kind of notion of MSLS you do have then?

Where can we find the definition of an MSLS

Nowhere, it seems. That's been my point the whole time. I'd love to see one too!

and the demonstration of the eliminations that the MSLS produces?

Does my previous post help at all? I'm very much a novice with MSLS, though. But if I got that right, then I guess I've just learned something.

In any case, this is David's original document about using MSLS. Unfortunately it skips the definition phase.

Added. The one thing that David, and pretty much everyone else except champagne, usually fail to mention is that you really need to understand Allan Barker's set logic for any of it to make sense. Both MSLS and Multi-Fish depend on it. (David just didn't admit it about MSLS.)

by **SpAce** » Tue Dec 03, 2019 11:20 am

champagne wrote:the answer is a practical view. 4 digits is likely the maximum for a human solver. In fact, often, a 5 digit multi-fish gives the same eliminations as another 4 digits multi fish.

Ok, thanks! Are the four multi-fish in my demo above correct and acceptable to you? They're the first multi-fishes I've spotted, or rather transformed from the MSLS I actually spotted. There are both 4-digit and 5-digit versions of the same thing, using both rows and columns (but no mix) as truths.

It seems to me that the right answer is more on the truths size (valid also for MSLS). In a human rank 0 logic (forget our friend "ttt" he can produce non human solutions) the truths size to search is in the range 12/20

Can a rectangular cell-based (naked) MSLS even be larger than 20 truths? Somehow it seems like the 4x5 must be the max size, but could there be larger ones too? Same question about the multi-fish.

by **pjb** » Tue Dec 03, 2019 11:48 am

Hi Robert

Regarding your request for working examples of MSLS's and also multifish, my website (philsfolly.net.au) can offer a large number of both. I started out basing my algorithms on posts by David Bird (SpAce has given links to him above) and gained a lot more insights from Leren in this forum.

Phil

by **Ajò Dimonios** » Tue Dec 03, 2019 1:23 pm

Hi at all
I would like to add a general question to what Robert did about MSLS. Can any of you tell me where to find the proof of the "Rank 0" law that Allan Barker mentions in his publication http://sudoku.allanbarker.com/sweb/general.htm. "Rank 0: Any non-base candidate contained in any link can be eliminated."?

thank you all
Paolo

by **SpAce** » Tue Dec 03, 2019 1:34 pm

Ajò Dimonios wrote:I would like to add a general question to what Robert did about MSLS. Can any of you tell me where to find the proof of the "Rank 0" law that Allan Barker mentions in his publication http://sudoku.allanbarker.com/sweb/general.htm. "Rank 0: Any non-base candidate contained in any link can be eliminated."?

What do you mean by proof? I think the reason is said pretty clearly right above it on that page, but I guess you don't count it as proof:

Allan Barker wrote:One simple approach uses the fact that there is one true candidate in each base set (truth). The number of true candidates is thus equal to the number of base sets. When all candidates in the base sets are covered by links, all the true candidates in the base sets must also be in the links.

In other words, if the number of links and truths is equal (Rank 0), every link must be occupied by a true base candidate. Thus all other candidates in the links must be false.

by **Ajò Dimonios** » Tue Dec 03, 2019 3:31 pm

Hi Space.
I wondered if there was a proof of this general law because for me it is not so immediate to establish its validity when the number of links and truths exceeds 4. Generally it is tempting to prove it by checking the combinations when the number of links and the number of truths is high but this is certainly not the way to face and solve the problem.

Ciao
Paolo

by **StrmCkr** » Tue Dec 03, 2019 4:39 pm

Code: Select all
Sets:
Bn = units of the base set
Base (size N): B = B1 + B2 ... + BN
Base Intersect: BI = B1*B2 + B1*B3 ... + B1*BN + B2*B3 ... + (BN-1)*BN

Cn = units of the cover set
Cover (size N): C = C1 + C2 ... + CN
Cover Intersect: CI = C1*C2 + C1*C3 ... + C1*CN + C2*C3 ... + (CN-1)*CN

Hidden Pattern: H = (B \ C) + BI
Exclusion: E = (C \ B) + CI

Symbol Key:
'+' <=> union ('|' in C++)
'*' <=> intersection ('&' in C++)
'\' <=> substraction ('X & ~Y' in C++)

Conjecture:

If the "hidden set" is empty,
then the "exclusion set" is empty also.

yes

1. exclusions in C\B

B will supply the digit N times (not less since none in BI);
all N will be in C (since none in B\C);
this supplies the full quota of the digit for the N units of C,
therefore, exclude it elswhere in C (i.e. in C\B).

2. exclusions in CI

placing the digit in CI would satisfy 2 (or more) units of C,
so C could only take N-1 of the total N supplied by B.

anyone wants to phrase it more formally?

User avatar
Pat

Posts: 3870
Joined: 18 July 2005

Top

Here you go, this is the math proof for rank zero+, muti fish, n fish, msls

Base count = cover count => rank 0.

by **Mauriès Robert** » Tue Dec 03, 2019 5:03 pm

Hi SpAce and Phil,
Thank you for your answers to my questions.
I know MSLS only through the discussions I had with Paolo (Ajò Dimonios ) on this subject and also by consulting Phil's website which I often use.
I understand that MSLS is a special provision G1 consisting of NxP cells located at the intersection of N rows and P columns, and meeting the following two conditions:

Condition 1)
E1 and E2 being two separate sets whose meeting E1UE2 is composed of the 9 occurrences 1,2, ...9;
The candidates of the NxP RiCj cells of G1 are distributed as shown in the figure below, where :
Aij = all RiCj candidates whose occurrences belong to E1.
Bij = all RiCj candidates whose occurrences belong to E2.

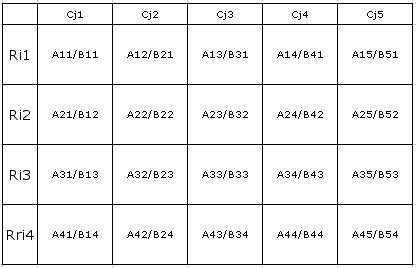
Condition 2)
- K1 being the sum in all the lines of G1, the number of occurrences of E1 already placed (revealed) and the number of occurrences of E1 that can be placed in these lines without leading to a contradiction in the lines of G1.
- K2 being the sum in all the columns of G1, the number of occurrences of E2 already placed (revealed) and the number of occurrences of E2 that can be placed in these columns without leading to a contradiction in CG1.
G1 is such that K1+ K2 = NxP (equilibrium)

Under two conditions I can demonstrate the eliminations associated with the MSLS.

However, I have difficulty seeing the relationship with Allan Parker's principles.
So I will read the writings of David Bird and Allan Parker to try to understand.

Sincerely
Robert

by **champagne** » Tue Dec 03, 2019 6:19 pm

Mauriès Robert wrote:Hi Champagne and SpAce,
I am not familiar with this notion of MSLS, so I have trouble following your discussions.
Where can we find the definition of an MSLS and the demonstration of the eliminations that the MSLS produces?
Thank you to you.
Robert

Hi Robert,
More after the previous answers if it can help.

I am not a specialist of the MSLS patterns, but let me try a "very simple" answer.

Just assume that we stay in the pure rank 0 logic, with sets limited to cells and "digit x unit" sets;
(in a set, one and only one candidate must be true).

In our pure rank 0 logic,
truths (base sets) are disjoints
links
hit all candidates of the sets
are disjoints

Note: to answer to another remark about a proof over 4 truths, in such a situation each assignment in a base set kills one base set and one linkset. after "n" assignments, all base sets and all linksets are assigned. There is no room for other assignments in the linksets.

2 well known simplest examples of such rank 0

one where the base is purely digit x unit is the Xwing
one where the base is purely cells is the pair of bi values cells in the same unit with 2 digits (naked pair).

In both cases of theses basic moves, the eliminations are well known by any sudoku player.

We have here the simplest "multi fish"and MSLS patterns.

To take the MSLS somehow simplest case, if considering a group of cells you can find linksets creating the rank 0 logic, then you can apply the rank 0 common rule.

As link sets can here only be digit x unit sets, the cells must be split in a limited number of rows; columns and boxes, the only way to have a possibility to build disjoints linksets hitting all base cells.

We see here that base cells could be in a box, not in a row/column matrix. I don't know if this is in the scope of David's MSLS patterns.

by **eleven** » Tue Dec 03, 2019 9:11 pm

Let me try it a bit more formal:

You have a sub-puzzle built by the crossing cells of some units (rows/columns, ev. boxes). I call them cells as usual,
Alan Barker called them truths, no idea why. [Edit: This is not the hole truth (thanks SpAce), Barker's truth is something more general. It is not needed here]

A so-called link consists of all occurances of a digit in a unit of the sub-puzzle, i.e. it is a group of same digit candidates in the same unit, thus linked by the unit.

A digit in one defined link must not be part of another link (as champagne said, they have to be disjoint).

If you can group all candidates of the sub-puzzle into disjoint links, and get as much links as you have cells, you have, what we talk about here.
(This is the hard part, when you want to find one)

Now trivially only one candidate of each link can be placed in the sub-puzzle.
And at least one candidate of each link must be placed to fill all cells.
(For completeness: The sub-puzzle must have at least one solution, i.e. a valid placements in all cells, if the puzzle has one).

So you can eliminate all candidates outside a link in the same unit of the puzzle.

by **SpAce** » Tue Dec 03, 2019 10:13 pm

Hi eleven,

eleven wrote:You have a sub-puzzle built by the crossing cells of some units (rows/columns, ev. boxes). I call them cells as usual, Alan Barker called them truths, no idea why.

Just to be sure, "truth" is not a synonym for cell (which is a term Allan uses perfectly normally):

Allan Barker wrote:A truth is any set of candidates where one candidate is part of the solution, i.e., a true candidate. Every Sudoku grid has 324 native truths, one truth for each of the 81 cells and 9 truths for each of the 9 rows, columns, and boxes.

In other words, what you choose as your truths (base sets) and links (cover sets) in a particular piece of logic depends on the point of view, as every one of those 324 containers can be used in either role.

Cells are truths only in the cell-centric MSNS and its simpler DDS subtypes (such as Sue de Coq) and of course basic one-sector naked subsets (all Rank 0 patterns), as well as Rank 1 patterns such as (UVW)X(YZ)-Wings, etc. Its opposite POV uses houses as truths, which gives you the "hidden" counterparts, including MSHS, hidden Sue de Coqs, and basic one-sector hidden subsets. In such hidden patterns cells are links. Single-digit fishes have both house-truths and house-links. Multi-Fishes use a combo of both (mostly house truths with possibly some cells mixed in, and the same for links). Generic AICs and nets can have any combinations, when written in set logic (i.e. as "Alien Fishes" in my terms).

by **eleven** » Tue Dec 03, 2019 10:46 pm

Please don't slay me with names.

I corrected my post concerning Alan's truths.
Now i remember, that exactly this definition of a truth let me stop reading many years ago. What should that be ? I pick 15 arbitrary candidates from the grid, and if one of them is part of the solution, that collection is a truth?

Concerning the hidden multisets: As you said, we cannot have the ones without the others. So do they need another proof ? If so, i am sure you can do it.

by **SpAce** » Tue Dec 03, 2019 11:19 pm

eleven wrote:Now i remember, that exactly this definition of a truth let me stop reading many years ago. What should that be ? I pick 15 arbitrary candidates from the grid, and if one of them is part of the solution, that collection is a truth?

I've never liked that unintuitive terminology either, but it is what it is. I would have preferred sticking to "base sets" and "cover sets", because they're at least somewhat understood by most who've used basic fishes. Anyway:

Code: Select all: "truth" <-> "base set" <-> "strong inference set" <-> "at least one must be true" "link " <-> "cover set" <-> "weak inference set" <-> "at most one can be true"

Native sets of candidates (cells, n-rows, n-cols, n-boxes) can be used in either role because they have exactly one true candidate. That's not true about derived strong and weak inference sets which are usually applicable in one or the other role only.

Concerning the hidden multisets: As you said, we cannot have the ones without the others. So do they need another proof ? If so, i am sure you can do it.

What do you mean? Did you see my horrible 39-truth MSHS transformations in this post?

The New Sudoku Players' Forum

SK-Loops and MSLS's

Re: SK-Loops and MSLS's

Re: SK-Loops and MSLS's

Re: SK-Loops and MSLS's

Re: triple point and rank 0 lgic

Re: SK-Loops and MSLS's

Re: SK-Loops and MSLS's

Re: SK-Loops and MSLS's

Re: SK-Loops and MSLS's

Re: SK-Loops and MSLS's

Re: SK-Loops and MSLS's

Re: SK-Loops and MSLS's

Re: SK-Loops and MSLS's

Re: SK-Loops and MSLS's

Re: SK-Loops and MSLS's

Re: SK-Loops and MSLS's