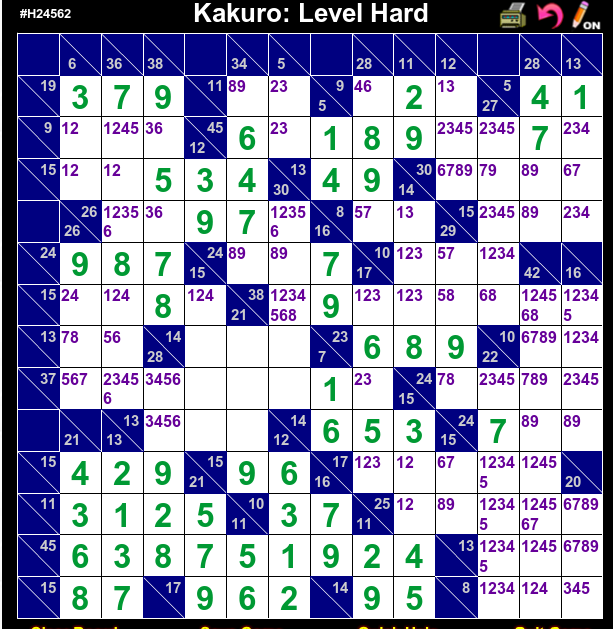
Well, I solved H24562 using trial and error, with the emphasis on error, but then I realized that it can be solved completely deductively, in hindsight. I had gotten to this point without T&E, which is about the point where I was stuck previously:
- H24562-1.png (94.13 KiB) Viewed 1583 times
(I think I probably accidentally erased a candidate, leading to an incorrect deduction.)
Anyway, I was stuck, so I decided to try T&E. I assumed r2c3 = 6, and after some time I got a contradiction:
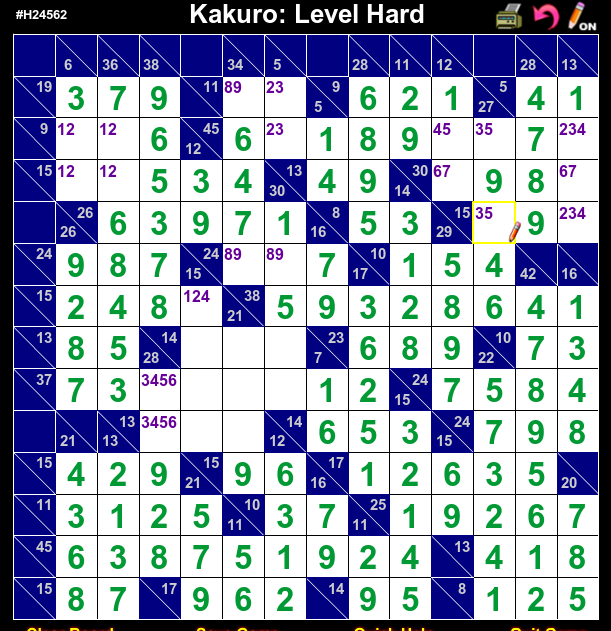
- H24562-2.png (91.93 KiB) Viewed 1583 times
Now I knew that r2c3 = 3, but that hardly propagated at all, except to tell me r2c2 = 45. (I use this notation to mean that r2c2 is one of 4 and 5.) I tried T&E again, therefore assuming r2c2=5 and got a contradiction, after about as much work as I'd needed before. Now however, the fact that r2c2 = 4, propagated to all parts of the puzzle, but I got a contradiction at the very end. I tried again, being as careful as I could, and once again got a contradiction. I therefore decided that I must have made a mistake after assuming r2c2 = 5. (Of course, I might have made a mistake earlier, but you're always stuck with the assumption that what you've done so far is correct, in chain kind of logical reasoning.)
Under that view of the matter, T&E and just shown r2c2<>4 so r2c2=5. I plugged that in again, and this time I was able to complete the puzzle.
While working the puzzle so many times, I noticed that under every path, I got r4c6 = 1, and that this had many consequences. I thought that if I could deduce this directly, I might be able to solve the puzzle without T&E. Go back to the first puzzle above, and note that in the first segment in row 4, the unknown cells must collective be 136 or 235. Suppose first that r4c6 = 36. Then r4c2=1, r3c2 = 2, r6c2 = 4, r2c2 = 5, r7c2 = 6. But then r7c1 = 7, so we must have r8c1 = 6, r6c1 = 4, but this is a contradiction, since we already decided r6c2 = 4. Now we can erase the candidates 3 and 6 from r4c6.
Suppose then that r4c6 = 25. Then r4c3 = 3, r2c3 = 6, and r2c2 = 12. Then we have the same contradiction as before, because r6c2 = 4, r2c2 = 5, r7c2 = 6, and we again have n r7c1 = 7, r8c1 = 6, r6c1 = 4.
At this point, we known that r4c6 = 1, and it turns out to be straightforward to complete the puzzle.
This is all easier to visualize that it may seem when written out, though I did it over in my head several times to be sure I wasn't making a mistake. Of course, I wouldn't even have tried this but for my experience with T&E.
Denis, do you happen to have analyzed this one?

