The New Sudoku Players' Forum

[Mathimagics]

Surprisingly there appears to be little information available on this topic - for a given grid size N, what is the minimum number of clues needed to fix a unique solution to a Futoshiki puzzle, or a Sudoshiki puzzle?

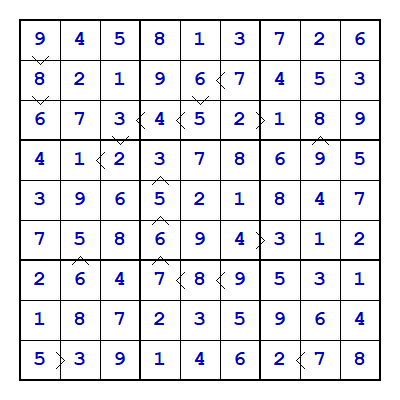
A Sudoshiki puzzle here is assumed to be a Futoshiki puzzle on a standard Sudoku grid (eg: 9 3x3 regions, 8 2x4 regions, 6 2x3 regions, etc).

Since clues can be in two forms - givens and relationships - a puzzle has 3 basic attributes:

• N - the grid size
• G - the number of givens
• R - the number of relationship clues (<, >)

A puzzle, FP(N, G, R) or SI(N, G, R) (SI for Sudoshiki, aka Sudoku Inequality) is minimal if removal of any given or relationship causes the puzzle to have multiple solutions.

My primary interest is in puzzles with G = 0, but I will in time take a look at puzzles with G > 0.

Searching for minimal cases is a time-consuming business, so my results for N > 5 are by no means definitive, but here they are:

Code: Select all

Minimal Futoshiki/Sudoshiki (no givens)

  N      R(FP)    R(SI)
----------------------- 
  4        4        3

  5        6

  6        9        8

  7       15

  8       24       19

  9       36       27



If anybody is aware of any examples of smaller R I'd be glad to hear from you, of course!

[Mathimagics]

Here is a case of SI(9, 0, 27):

Minimal Sudoshiki, N = 9, G = 0, R = 27

SImin9_R27.jpg (21.49 KiB) Viewed 2260 times

Solution:

Hidden Text: Show

456289173
318476259
729531468
934712586
581643792
672958341
243867915
165394827
897125634

[Mathimagics]

The smallest R for which an FP(7, 0, R) has been found so far is 15. Here is one example:

Example #7a: FP(N=7, G=0, R=15)

Fmin7_G0_R15.jpg (13.49 KiB) Viewed 2235 times

Solution:

Hidden Text: Show

7134256
4325761
6413572
1547623
2761345
3256417
5672134

[Mathimagics]

Now consider the following table, where we consider min R for various G:

Code: Select all

Minimal R for N = 7
-------------- 
  G     R
-------------- 
  0    15
  1    14
  2    13 
  3    12
  4    11   (example given below)
  5    10
  6     9


These are the minimal R cases found so far for given G, after a week of 4-core searching. We might be forgiven for thinking that the total hints, H = G + R, is always at least 15, however this is demonstrably false.

Consider cases at the other extreme, ie. with R = 0. These correspond to standard Latin Square/Sudoku puzzles, and hence minimal G corresponds to the size of the smallest critical set for the given solution. For N = 7 we know that G can be as low as 12.

Also, for standard Sudoku we know that G can be as low as 17, whereas the smallest R we have found so far, (ie: for G = 0), is 27.

Here is an example of an FP(7, 4, 11) puzzle:

Example #7b: FP(N=7, G=4, R=11)

Fmin7_G4_R11.jpg (14.16 KiB) Viewed 2235 times

Solution:

Hidden Text: Show

6135247
1467352
5713624
2351476
7246135
4672513
3524761

[Pat]

A Sudoshiki puzzle here is assumed to be a Futoshiki puzzle on a standard Sudoku grid (eg: 9 3x3 regions, 8 2x4 regions, 6 2x3 regions, etc)

or include jigSu-shiki ?
(Futoshiki in a jigsaw-SuDoku)

advantage —
allows all puzzle-sizes (e.g. 7-squared)

but a vast task,
to review all possible box-shapes for jigsaw——

[Mathimagics]

or include jigSu-shiki ? (Futoshiki in a jigsaw-SuDoku)

SudokuXtra refers to these as "Jigsaw Inequality" puzzles. I'll call them JI for short, to go with FP and SI.

but a vast task, to review all possible box-shapes for jigsaw——

Indeed! By my count, for N = 7, there are 158,747,952 different (contiguous) jigsaw layouts to consider.

We do know that JI(N, N-1, 0) puzzles exist, ie. with G = N - 1 and R = 0. And conversely, JI(N, 0, N-1) puzzles exist, also (although not very interesting ones).

[Mathimagics]

I have found cases of 14-hint puzzles for N = 7.

These were found by looking at FP(7, 14, 0) instances, ie: latin squares of order 7 with MCS = 14 (Minimal Critical Set size).

I then used a GR-trade process - this involves trying to replace givens with relationships, ie {-G, +R}. This is still a slow process, since all symbol-permutations need to be considered, but it is at least a focused one.

The largest trade discovered so far is 10 - ie: we get a FP(7, 4, 10) puzzle. One example is given below:

[ EDIT ] this image deleted 23/10/2021

Solution:

Hidden Text: Show

7654312
1423576
3542761
4165237
5371624
6217453
2736145

[Mathimagics]

For N = 7, we know that the smallest known MCS is 12, so theoretically we have 12-hint puzzles possible.

These cases are less productive. The underlying latin square has one basic form, ie. each row/col is simply a rotation of the first (the basic form is the back-circulant LS). I did find one trade of size 4, which gives a G=8, R=4 puzzle:

N = 7, G = 8, R = 4

Fmin7_G8_R4.jpg (14.23 KiB) Viewed 2216 times

Solution:

Hidden Text: Show

7364251
3642517
6425173
4251736
2517364
5173642
1736425

[blue]

Here are some more G=0, "low R" puzzles -- no idea if the R's are the minimums for G=0.
They're in the format that you and Denis Berthier developed.
For 6x6 and 8x8 Sudoshiki, the layout is with boxes that are 2 cells tall by 3 or 4 cells wide.

Code: Select all

Futoshiki:

7x7 - 12 clues
---<---------------------<-<>----<--------
--->---------->>--------->>>------>-------

8x8 - 18 clues
------>--------<--->--------------><--<-----------------
----->>-->>>----------<----------<---<<---<<------<-----

9x9 - 24 clues
-----------<<-----<---<<---<----<-------<------->--------->-->>-->-<----
----->-------->>-->----<->--<----------------->--->-------------->------

Sudoshiki:

6x6 - 7 clues
--------<------>---------->>--
-------->>------>-------------

8x8 - 15 clues
----------<----------<--->>------<---------------->---->
--<--------<----->---->--------------------->>------>>--

9x9 - 19 clues
------------<-----<<->---<------------------->-----<<----------->-----<-
>>-----------<---->--------<<<--->------------------------<-------------


[Mathimagics]

Great work, blue!

My search technique clearly leaves something to be desired! How did you find these?

Updated table:

Code: Select all

Minimal Relationships (no givens)

      Futoshiki Sudoshiki
  N        R        R 
----------------------- 
  4        4        3
  5        6
  6        9        7
  7       12
  8       18       15
  9       24       19


[Mathimagics]

.
Update (2 June 2022)

Following some recent postings related to this topic, I have finally built a SAT solver for Sudoshiki (aka Sudoku Greater Than, Sudoku Inequality), and on checking the 19R example given by blue above, I find that puzzle to be invalid (multiple solutions):

Code: Select all

Blue: 9x9 - 19 clues
------------<-----<<->---<------------------->-----<<----------->-----<-
>>-----------<---->--------<<<--->------------------------<-------------

Base Clause count = 11988
Clause count = 12672, Ineqs = 19
Solving GT
NS = 2 (maybe more)
792413865165829734843675129237961458659384217418257693524138976381796542976542381
792413865165829734843675129237961458659384217418257693524138976386792541971546382


I have verified that both of these solutions reported by the solver are valid.

[creint]

Code: Select all

Blue: 9x9 - 19 clues
------------<-----<<->---<------------------->-----<<----------->-----<-
>>-----------<---->--------<<<--->------------------------<-------------

Has an single solution confirmed by logic < SE 10 and SAT solvers:

Code: Select all

9 4 5 8 1 3 7 2 6
8 2 1 9 6 7 4 5 3
6 7 3 4 5 2 1 8 9
4 1 2 3 7 8 6 9 5
3 9 6 5 2 1 8 4 7
7 5 8 6 9 4 3 1 2
2 6 4 7 8 9 5 3 1
1 8 7 2 3 5 9 6 4
5 3 9 1 4 6 2 7 8

You could have pasted this in my solver (in newer versions empty grid not required):

Code: Select all

.................................................................................
------------<-----<<->---<------------------->-----<<----------->-----<-
>>-----------<---->--------<<<--->------------------------<-------------

After running Sat4J or MiniSatExe you can get the cnf which in this case is 11215 clauses.

In your solution 1
r2c56 contradicts r2c5 > r2c6
r12c1 contradicts r1c1 > r1c2
Totaling 6 vertical conflicts.

[Mathimagics]

.
Hi creint!

Thanks for that info, that helped me identify the problem immediately - we are using different puzzle string forms.

I have always used left-to-right, row by row format for both the horizontal and vertical clue strings. That makes it easier (for me, at least) to build strings from puzzle images.

You, and blue have both used top-down, column by column, for the vertical clue string.

So for blue's 19 clue spec:

Code: Select all

------------<-----<<->---<------------------->-----<<----------->-----<-
>>-----------<---->--------<<<--->------------------------<-------------


To use in my solver & image rendering I need to convert that to:

Code: Select all

------------<-----<<->---<------------------->-----<<----------->-----<-
>-------->--->------>----<----<--------<------<-<-----------------------


And hey, presto, I now find the unique solution that you identified.

Cheers
MM

[Mathimagics]

I have finally found a painless way to "publish" images so I no longer have to rely on attachments.

So here is blue's record-setting 19-clue Sudoshiki, with its solution:

[blue]

Hi guys,

Will one or both of you please confirm that this one is valid too ?

Code: Select all

17-clue 9x9 Sudoshiki

.................................................................................
----------<------<--------->---->---------------->---<---->>-->---------
------------>>----<--->->-------------->----------->----->--------------

+-----------+-----------+-----------+
| .   .   . | .   .   . | .   .   . |
|           | v         |           |
| .   .   . < .   .   . | .   .   . |
|           |           |     v     |
| .   . < . | .   .   . | .   .   . |
+-------- ^ +-----------+-----------+
| .   .   . | . > .   . | .   .   . |
|           |           | v         |
| . > .   . | .   .   . | .   .   . |
|     v     |           |           |
| .   .   . | .   .   . | .   .   . |
+---- v ----+-----------+-----------+
| .   . > . | .   .   . < .   .   . |
|         v |           |           |
| .   .   . > . > .   . | . > .   . |
|           |     v     |           |
| .   .   . | .   .   . | .   .   . |
+-----------+-----------+-----------+

Solution:

Hidden Text: Show

Code: Select all

158964327497832561623175849346751298982643175571298634265487913814329756739516482

+-----------+-----------+-----------+
| 1   5   8 | 9   6   4 | 3   2   7 |
|           | v         |           |
| 4   9   7 < 8   3   2 | 5   6   1 |
|           |           |     v     |
| 6   2 < 3 | 1   7   5 | 8   4   9 |
+-------- ^ +-----------+-----------+
| 3   4   6 | 7 > 5   1 | 2   9   8 |
|           |           | v         |
| 9 > 8   2 | 6   4   3 | 1   7   5 |
|     v     |           |           |
| 5   7   1 | 2   9   8 | 6   3   4 |
+---- v ----+-----------+-----------+
| 2   6 > 5 | 4   8   7 < 9   1   3 |
|         v |           |           |
| 8   1   4 > 3 > 2   9 | 7 > 5   6 |
|           |     v     |           |
| 7   3   9 | 5   1   6 | 4   8   2 |
+-----------+-----------+-----------+


Cheers,
Blue.

Edit: Fixed the solution. It was for a different puzzle !
Thanks Colin.