The New Sudoku Players' Forum

[denis_berthier]

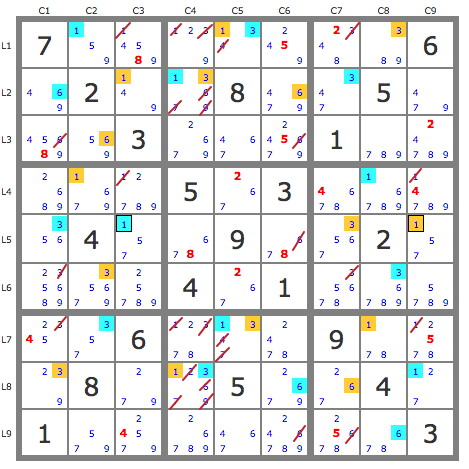
Code: Select all

   +-------+-------+-------+
   ! 7 . . ! . . . ! . . 6 !
   ! . 2 . ! . 8 . ! . 5 . !
   ! . . 3 ! . . . ! 1 . . !
   +-------+-------+-------+
   ! . . . ! 5 . 3 ! . . . !
   ! . 4 . ! . 9 . ! . 2 . !
   ! . . . ! 4 . 1 ! . . . !
   +-------+-------+-------+
   ! . . 6 ! . . . ! 9 . . !
   ! . 8 . ! . 5 . ! . 4 . !
   ! 1 . . ! . . . ! . . 3 !
   +-------+-------+-------+


7.......6.2..8..5...3...1.....5.3....4..9..2....4.1.....6...9...8..5..4.1.......3
SER = 8.9


[Leren]

Code: Select all

*--------------------------------------------------------------------------------*
| 7       159     458-19   | 1239    13      2459     | 248-3   389     6        |
|*469     2      *149      | 13679   8       679-4    |*347     5      *479      |
| 458-69  569     3        | 2679    467     245679   | 1       789     248-79   |
|--------------------------+--------------------------+--------------------------|
|*2689    1679   *12789    | 5       267     3        |*4678    1679-8 *14789    |
|*356     4      *157      | 678     9       678      |*3567    2      *157      |
|*235689  3679-5 *25789    | 4       267     1        |*35678   3679-8 *5789     |
|--------------------------+--------------------------+--------------------------|
| 245-3   357     6        | 12378   13      2478     | 9       178     258-17   |
|*239     8      *279      | 13679-2 5       679-2    |*267     4      *127      |
| 1       579     245-79   | 26789   467     246789   | 258-67  678     3        |
*--------------------------------------------------------------------------------*

You can start out with a Multifish or MSLS. This MSLS has 20 Cells r24568 c1379 : 20 Links; 4r2 48r4 5r5 58r6 & 2r8 ; 369c1 179c3 367c7 179c9 ; 2b4 ; 20 eliminations as marked. Haven't worked out a cute finish yet . Leren

<edit> Moved eliminations from Row 4 to Row 3. Thanks to SpAce for spotting the typo. Leren

[pjb]

Just to be different, I found a "variant" SK loop with same 20 eliminations. Apologies if the loop troubles you.

Variant SK loop: (4=169)r2c13 - (169=5)r13c2 - (5=379)r79c2 - (379=2)r8c13 - (2=167)r8c79 - (167=8)r79c8 - (8=379)r13c8 - (379=4)r2c79 - loop
Following I could only find a tedious sequence of forcing chains, ALSs, etc which I won't bore you with.
Phil

[Ajò Dimonios]

27 eliminations by crossing the conjugate tracks T (1r4c8) and T (1r7c8)

[SpAce]

I think Phil's "variant SK-Loop" is the most obvious opening volley here, hinted by the box-diagonals. Here presented as a non-rectangular MSLS and a mutant Multifish:

Code: Select all

  \b1:169          \b7:379                          \b3:379           \b9:167
           \5                                                \8
.--------------------------.----------------------.---------------------------.
|  7       *159     458-19 | 1239     13   2459   |  248-3   *389      6      |
| *469      2      *149    | 13679    8    679-4  | *347      5       *479    | \4
|  458-69  *569     3      | 2679     467  245679 |  1       *789      248-79 |
:--------------------------+----------------------+---------------------------:
|  2689     1679    12789  | 5        267  3      |  4678     1679-8   14789  |
|  356      4       157    | 678      9    678    |  3567     2        157    |
|  235689   3679-5  25789  | 4        267  1      |  35678    3679-8   5789   |
:--------------------------+----------------------+---------------------------:
|  245-3   *357     6      | 12378    13   2478   |  9       *178      258-17 |
| *239      8      *279    | 13679-2  5    679-2  | *267      4       *127    | \2
|  1       *579     245-79 | 26789    467  246789 |  258-67  *678      3      |
'--------------------------'----------------------'---------------------------'

MSLS: 16x16 {28N1379 1379N28 \ 2r8 4r2 5c2 8c8 169b1 379b3 379b7 167b9} => 20 elims

Code: Select all

  \b1:169  \46n    \b7:379                            \b3:379  \46n     \b9:167
           *13679                                              *13679
.--------------------------.------------------------.---------------------------.
|  7^       159     458-19 |  1239     13    2459   |  248-3    389      6^     |
|  469      2       149    | \13679    8    \679-4  |  347      5        479    | *13679  \n46
|  458-69   569     3^     |  2679     467   245679 |  1^       789      248-79 |
:--------------------------+------------------------+---------------------------:
|  2689    \1679    12789  |  5        267   3^     |  4678    \1679-8   14789  |
|  356      4       157    |  678      9^    678    |  3567     2        157    |
|  235689  \3679-5  25789  |  4        267   1^     |  35678   \3679-8   5789   |
:--------------------------+------------------------+---------------------------:
|  245-3    357     6^     |  12378    13    2478   |  9^       178      258-17 |
|  239      8       279    | \13679-2  5    \679-2  |  267      4        127    | *13679  \n46
|  1^       579     245-79 |  26789    467   246789 |  258-67   678      3^     |
'--------------------------'------------------------'---------------------------'

MF (13679 RC): 20x20 {13679R28 13679C28 \ 169b1 379b3 379b7 167b9 46n28 28n46} => 20 elims (the same)

--
They're the same eliminations as with Leren's MSLS.

The rest is probably not interesting, but I'll be glad to stand corrected.

--
Edit. Corrected a typo of my own: in both grids b1:139 --> b1:169.

[Mauriès Robert]

Hi all,
He will have escaped to nobody the beautiful loops on the 1's and 3's which, taken separately, generate 12 eliminations (six 1's and six 3's). But, as Paolo points out, with two tracks generated by a pair of 1's (strongly linked) it is 27 eliminations that we get as we see on the puzzle1.
Note that both tracks have 15 marked candidates each.
Robert

puzzle1: Show

[Leren]

Code: Select all

*--------------------------------------------------------------------------------*
| 7       159     458      | 29      13      2459     | 248     389     6        |
| 469     2       149      | 13      8       679      | 347     5       479      |
| 58      569     3        | 2679    467     245679   | 1       789     248      |
|--------------------------+--------------------------+--------------------------|
| 2689    1679    2789     | 5       267     3        | 4678    1679    4789     |
| 356     4       157      | 678     9       678      | 3567    2       157      |
| 25689   3679    25789    | 4       267     1        | 5678    3679    5789     |
|--------------------------+--------------------------+--------------------------|
| 245     357     6        | 278     13      2478     | 9       178     258      |
| 239     8       279      | 13      5       679      | 267     4       127      |
| 1       579     245      | 26789   467     246789   | 258     678     3        |
*--------------------------------------------------------------------------------*

After the MSLS/Multifish/SK Loop I found Swordfishes on 1 and 3, an M ring and a Skyscraper, that gets to this position.

As Phil said, after that it gets very tedious. Hodoku agrees. Maybe denis can show us the way. Leren

[denis_berthier]

The original puzzle is in W7. If you want the full resolution path from the start, just ask me.
The underlying pattern is as symmetric as one may hope and it can therefore be expected to have some special elimination rules. But do they simplify it much?

I'll start with Leren's first PM, after his 20 eliminations:

Code: Select all

(solve-sukaku-grid
   *--------------------------------------------------------------------------------*
   ! 7       159     458      ! 1239    13      2459     ! 248     389     6        !
   ! 469     2       149      ! 13679   8       679      ! 347     5       479      !
   ! 458     569     3        ! 2679    467     245679   ! 1       789     248      !
   !--------------------------+--------------------------+--------------------------!
   ! 2689    1679   12789     ! 5       267     3        ! 4678    1679   14789     !
   ! 356     4      157       ! 678     9       678      ! 3567    2      157       !
   ! 235689  3679   25789     ! 4       267     1        ! 35678   3679   5789      !
   !--------------------------+--------------------------+--------------------------!
   ! 245     357     6        ! 12378   13      2478     ! 9       178     258      !
   ! 239     8      279       ! 13679   5       679      ! 267     4      127       !
   ! 1       579     245      ! 26789   467     246789   ! 258     678     3        !
   *--------------------------------------------------------------------------------*
)

The gain can't be neglected, as we jump down from W7 to W5. Nevertheless, the end is not very simple.

Code: Select all

***********************************************************************************************
***  SudoRules 20.1.s based on CSP-Rules 2.1.s, config = W+SFin
***  Using CLIPS 6.32-r774
***********************************************************************************************
215 candidates, 1247 csp-links and 1247 links. Density = 5.42%
finned-x-wing-in-columns: n4{c5 c3}{r9 r3} ==> r3c1 ≠ 4
swordfish-in-columns: n3{c2 c5 c8}{r6 r7 r1} ==> r7c4 ≠ 3, r6c7 ≠ 3, r6c1 ≠ 3, r1c4 ≠ 3
swordfish-in-columns: n1{c2 c5 c8}{r4 r1 r7} ==> r7c4 ≠ 1, r4c9 ≠ 1, r4c3 ≠ 1, r1c4 ≠ 1
hidden-pairs-in-a-block: b2{r1c5 r2c4}{n1 n3} ==> r2c4 ≠ 9, r2c4 ≠ 7, r2c4 ≠ 6
hidden-pairs-in-a-column: c4{n1 n3}{r2 r8} ==> r8c4 ≠ 9, r8c4 ≠ 7, r8c4 ≠ 6
whip[4]: b3n2{r3c9 r1c7} - r1n8{c7 c3} - r1n4{c3 c6} - r3n4{c5 .} ==> r3c9 ≠ 8
z-chain[3]: r3c9{n2 n4} - b2n4{r3c5 r1c6} - c6n5{r1 .} ==> r3c6 ≠ 2
whip[5]: c1n4{r7 r2} - b1n6{r2c1 r3c2} - c2n5{r3 r1} - b1n1{r1c2 r2c3} - b1n9{r2c3 .} ==> r7c1 ≠ 5
biv-chain[4]: r7n5{c9 c2} - r7n3{c2 c5} - r8c4{n3 n1} - c9n1{r8 r5} ==> r5c9 ≠ 5
biv-chain[4]: r5c9{n7 n1} - c3n1{r5 r2} - r2c4{n1 n3} - c7n3{r2 r5} ==> r5c7 ≠ 7
z-chain[5]: c7n3{r5 r2} - r2c4{n3 n1} - c3n1{r2 r5} - r5n5{c3 c1} - r5n3{c1 .} ==> r5c7 ≠ 6
whip[5]: b9n1{r7c8 r8c9} - r5c9{n1 n7} - c7n7{r6 r2} - r2n3{c7 c4} - c4n1{r2 .} ==> r7c8 ≠ 7
biv-chain[3]: r7c8{n8 n1} - r7c5{n1 n3} - r1n3{c5 c8} ==> r1c8 ≠ 8
whip-bn[4]: b3n2{r3c9 r1c7} - b3n8{r1c7 r3c8} - b9n8{r7c8 r9c7} - b9n5{r9c7 .} ==> r7c9 ≠ 2
t-whip[4]: r1n8{c7 c3} - r3c1{n8 n5} - r1n5{c3 c6} - r1n4{c6 .} ==> r1c7 ≠ 2
hidden-single-in-a-block ==> r3c9 = 2
whip[1]: r3n4{c6 .} ==> r1c6 ≠ 4
naked-pairs-in-a-column: c9{r5 r8}{n1 n7} ==> r6c9 ≠ 7, r4c9 ≠ 7, r2c9 ≠ 7
hidden-pairs-in-a-row: r1{n4 n8}{c3 c7} ==> r1c3 ≠ 5
biv-chain[4]: b3n7{r3c8 r2c7} - r2n3{c7 c4} - r8c4{n3 n1} - r8c9{n1 n7} ==> r9c8 ≠ 7
whip[1]: b9n7{r8c9 .} ==> r8c3 ≠ 7, r8c6 ≠ 7
whip[1]: b7n7{r9c2 .} ==> r4c2 ≠ 7, r6c2 ≠ 7
biv-chain[4]: c1n4{r7 r2} - r2n6{c1 c6} - r8c6{n6 n9} - r8c3{n9 n2} ==> r7c1 ≠ 2
naked-single ==> r7c1 = 4
whip[1]: r7n2{c6 .} ==> r9c4 ≠ 2, r9c6 ≠ 2
biv-chain[4]: r2c9{n4 n9} - r1c8{n9 n3} - r2n3{c7 c4} - r2n1{c4 c3} ==> r2c3 ≠ 4
singles ==> r1c3 = 4, r1c7 = 8, r3c1 = 8
whip[1]: c1n5{r6 .} ==> r5c3 ≠ 5, r6c3 ≠ 5
singles ==> r9c3 = 5, r9c7 = 2, r7c9 = 5
naked-pairs-in-a-row: r5{c3 c9}{n1 n7} ==> r5c6 ≠ 7, r5c4 ≠ 7
whip[1]: b5n7{r6c5 .} ==> r3c5 ≠ 7, r9c5 ≠ 7
naked-pairs-in-a-column: c5{r3 r9}{n4 n6} ==> r6c5 ≠ 6, r4c5 ≠ 6
whip[1]: b5n6{r5c6 .} ==> r5c1 ≠ 6
biv-chain[3]: r8c6{n9 n6} - r8c7{n6 n7} - r2n7{c7 c6} ==> r2c6 ≠ 9
biv-chain[3]: r2c6{n7 n6} - r3c5{n6 n4} - r9n4{c5 c6} ==> r9c6 ≠ 7
biv-chain[3]: r2c6{n7 n6} - b1n6{r2c1 r3c2} - r3n5{c2 c6} ==> r3c6 ≠ 7
biv-chain[3]: c6n4{r3 r9} - r9c5{n4 n6} - r8c6{n6 n9} ==> r3c6 ≠ 9
biv-chain[3]: r5c6{n8 n6} - r8n6{c6 c7} - r9c8{n6 n8} ==> r9c6 ≠ 8
naked-triplets-in-a-block: b8{r8c6 r9c5 r9c6}{n9 n6 n4} ==> r9c4 ≠ 9, r9c4 ≠ 6
whip[1]: b8n9{r9c6 .} ==> r1c6 ≠ 9
biv-chain[3]: r9n9{c2 c6} - c6n4{r9 r3} - r3n5{c6 c2} ==> r3c2 ≠ 9
hidden-pairs-in-a-row: r3{n7 n9}{c4 c8} ==> r3c4 ≠ 6
singles ==> r5c4 = 6, r5c6 = 8
biv-chain[4]: r1c8{n9 n3} - r6n3{c8 c2} - r7c2{n3 n7} - r9c2{n7 n9} ==> r1c2 ≠ 9
whip[1]: b1n9{r2c3 .} ==> r2c9 ≠ 9
singles ==> r2c9 = 4, r4c7 = 4
whip[1]: c9n9{r6 .} ==> r4c8 ≠ 9, r6c8 ≠ 9
biv-chain[3]: r2n9{c3 c1} - r2n6{c1 c6} - r8c6{n6 n9} ==> r8c3 ≠ 9
naked-single ==> r8c3 = 2
biv-chain-rc[4]: r2c6{n7 n6} - r8c6{n6 n9} - r8c1{n9 n3} - r7c2{n3 n7} ==> r7c6 ≠ 7
stte

Note that the result isn't very different if I start from Leren's second PM (still in W5)


Hard world, isn't it?
Now I wonder: why did no-one come out with a full solution based on set coverings similar to those providing the first eliminations? Why do all these solvers work only for the largest coverings? What's missing in the covering algorithms?

[Leren]

Hi denis. The simple answer to your question is that all the fancy MSLS, Multifish, SK Loops etc are all Rank 0 moves, and this does not happen to be a Rank 0 friendly puzzle.

Mith has been feeding us with a lot of Rank 0 friendly puzzles recently and we've got all gotten lazy. Faced with a lot of chipping away to complete the puzzle, nobody really tried, except you.

Solving a puzzle with lots of moves, whilst minimising the complexity of each move at each point is what you have been demonstrating all along. A salutary lesson for the rest of us.

Leren

PS - chipping away with more moves in my solver but not forcing chains I can get to the following PM

Code: Select all

*--------------------------------------------------------------------------------*
| 7       159     458      | 29      13      2459     | 248     389     6        |
| 469     2       149      | 13      8       679      | 347     5       479      |
| 58      569     3        | 2679    467     45679    | 1       789     24       |
|--------------------------+--------------------------+--------------------------|
| 2689    1679    2789     | 5       267     3        | 4678    1679    4789     |
| 356     4       157      | 678     9       678      | 35      2       17       |
| 25689   3679    25789    | 4       267     1        | 5678    3679    5789     |
|--------------------------+--------------------------+--------------------------|
| 24      357     6        | 278     13      2478     | 9       178     58       |
| 239     8       279      | 13      5       679      | 267     4       127      |
| 1       579     245      | 26789   467     246789   | 258     678     3        |
*--------------------------------------------------------------------------------*

This has 7 fewer candidates than the previous one. Pasting this into Hodoku, it's first move is a (very tedious) forcing chain:

Forcing Chain Contradiction in c3 => r3c9=2r3c9<>2 r3c9=4 r2c79<>4 r2c13=4 r1c3<>4r3c9<>2 r8c9=2 r8c9<>1 r8c4=1 r2c4<>1 r2c3=1 r2c3<>4r3c9<>2 r3c9=4 r3c5<>4 r9c5=4 r9c3<>4

and there is lots more besides, the Hodoku score from that point being 4086. The Hodoku score for the original puzzle was 7830, so I simplified things a bit, but not too much.

Leren

[denis_berthier]

Hi denis. The simple answer to your question is that all the fancy MSLS, Multifish, SK Loops etc are all Rank 0 moves, and this does not happen to be a Rank 0 friendly puzzle.

Sure. But rank 0 puzzles are a statistical minority.

Mith has been feeding us with a lot of Rank 0 friendly puzzles recently and we've got all gotten lazy. Faced with a lot of chipping away to complete the puzzle, nobody really tried, except you.

I loved Mith's exceptional puzzles and I think many Sudoku players out there loved them, because they involve so many Subsets. I understand you've probably gotten lazy with them because you've already done too many of them. But don't forget the vast majority of players who don't spend their lives playing Sudoku, who hardly know what a Subset is and who still enjoy finding them. In the past years, this forum has become too navel-gazing.

Solving a puzzle with lots of moves, whilst minimising the complexity of each move at each point is what you have been demonstrating all along. A salutary lesson for the rest of us.

So, if understand you well: you are tired of rank 0 puzzles, you don't want to consider other puzzles involving different patterns, you need some novelty. What options are you left with? Time to try different kinds of puzzles (Kakuro, Futoshiki, ...)?

[denis_berthier]

Just seen your P.S.

PS - chipping away with more moves in my solver but not forcing chains I can get to the following PM

Code: Select all

*--------------------------------------------------------------------------------*
| 7       159     458      | 29      13      2459     | 248     389     6        |
| 469     2       149      | 13      8       679      | 347     5       479      |
| 58      569     3        | 2679    467     45679    | 1       789     24       |
|--------------------------+--------------------------+--------------------------|
| 2689    1679    2789     | 5       267     3        | 4678    1679    4789     |
| 356     4       157      | 678     9       678      | 35      2       17       |
| 25689   3679    25789    | 4       267     1        | 5678    3679    5789     |
|--------------------------+--------------------------+--------------------------|
| 24      357     6        | 278     13      2478     | 9       178     58       |
| 239     8       279      | 13      5       679      | 267     4       127      |
| 1       579     245      | 26789   467     246789   | 258     678     3        |
*--------------------------------------------------------------------------------*

This has 7 fewer candidates than the previous one. Pasting this into Hodoku, it's first move is a (very tedious) forcing chain:

Forcing Chain Contradiction in c3 => r3c9=2r3c9<>2 r3c9=4 r2c79<>4 r2c13=4 r1c3<>4r3c9<>2 r8c9=2 r8c9<>1 r8c4=1 r2c4<>1 r2c3=1 r2c3<>4r3c9<>2 r3c9=4 r3c5<>4 r9c5=4 r9c3<>4

Is this supposed to be a single chain (of length 9)?
If so, Hodoku is pretty bad at this point, as it misses a much shorter chain (length 5):

Code: Select all

(solve-sukaku-grid
   *--------------------------------------------------------------------------------*
   ! 7       159     458      ! 29      13      2459     ! 248     389     6        !
   ! 469     2       149      ! 13      8       679      ! 347     5       479      !
   ! 58      569     3        ! 2679    467     45679    ! 1       789     24       !
   !--------------------------+--------------------------+--------------------------!
   ! 2689    1679    2789     ! 5       267     3        ! 4678    1679    4789     !
   ! 356     4       157      ! 678     9       678      ! 35      2       17       !
   ! 25689   3679    25789    ! 4       267     1        ! 5678    3679    5789     !
   !--------------------------+--------------------------+--------------------------!
   ! 24      357     6        ! 278     13      2478     ! 9       178     58       !
   ! 239     8       279      ! 13      5       679      ! 267     4       127      !
   ! 1       579     245      ! 26789   467     246789   ! 258     678     3        !
   *--------------------------------------------------------------------------------*
)

***********************************************************************************************
***  SudoRules 20.1.s based on CSP-Rules 2.1.s, config = W+SFin
***  Using CLIPS 6.32-r774
***********************************************************************************************
193 candidates, 988 csp-links and 988 links. Density = 5.33%
whip[5]: b9n1{r7c8 r8c9} - c4n1{r8 r2} - r2n3{c4 c7} - b3n7{r2c7 r2c9} - r5c9{n7 .} ==> r7c8 ≠ 7
biv-chain[3]: r7c8{n8 n1} - r7c5{n1 n3} - r1n3{c5 c8} ==> r1c8 ≠ 8
t-whip[4]: r1n8{c7 c3} - r3c1{n8 n5} - r1n5{c3 c6} - r1n4{c6 .} ==> r1c7 ≠ 2
hidden-single-in-a-block ==> r3c9 = 2
whip[1]: r3n4{c6 .} ==> r1c6 ≠ 4
naked-pairs-in-a-column: c9{r5 r8}{n1 n7} ==> r6c9 ≠ 7, r4c9 ≠ 7, r2c9 ≠ 7
hidden-pairs-in-a-row: r1{n4 n8}{c3 c7} ==> r1c3 ≠ 5
biv-chain[4]: b3n7{r3c8 r2c7} - r2n3{c7 c4} - r8c4{n3 n1} - r8c9{n1 n7} ==> r9c8 ≠ 7
whip[1]: b9n7{r8c9 .} ==> r8c3 ≠ 7, r8c6 ≠ 7
whip[1]: b7n7{r9c2 .} ==> r4c2 ≠ 7, r6c2 ≠ 7
biv-chain[4]: c1n4{r7 r2} - r2n6{c1 c6} - r8c6{n6 n9} - r8c3{n9 n2} ==> r7c1 ≠ 2
naked-single ==> r7c1 = 4
whip[1]: r7n2{c6 .} ==> r9c4 ≠ 2, r9c6 ≠ 2
biv-chain[4]: r2c9{n4 n9} - r1c8{n9 n3} - r2n3{c7 c4} - r2n1{c4 c3} ==> r2c3 ≠ 4
singles ==> r1c3 = 4, r1c7 = 8, r3c1 = 8
whip[1]: c1n5{r6 .} ==> r5c3 ≠ 5, r6c3 ≠ 5
singles ==> r9c3 = 5, r9c7 = 2, r7c9 = 5
naked-pairs-in-a-row: r5{c3 c9}{n1 n7} ==> r5c6 ≠ 7, r5c4 ≠ 7
whip[1]: b5n7{r6c5 .} ==> r3c5 ≠ 7, r9c5 ≠ 7
naked-pairs-in-a-column: c5{r3 r9}{n4 n6} ==> r6c5 ≠ 6, r4c5 ≠ 6
whip[1]: b5n6{r5c6 .} ==> r5c1 ≠ 6
biv-chain[3]: r8c6{n9 n6} - r8c7{n6 n7} - r2n7{c7 c6} ==> r2c6 ≠ 9
biv-chain[3]: r2c6{n7 n6} - r3c5{n6 n4} - r9n4{c5 c6} ==> r9c6 ≠ 7
biv-chain[3]: r2c6{n7 n6} - b1n6{r2c1 r3c2} - r3n5{c2 c6} ==> r3c6 ≠ 7
biv-chain[3]: c6n4{r3 r9} - r9c5{n4 n6} - r8c6{n6 n9} ==> r3c6 ≠ 9
biv-chain[3]: r5c6{n8 n6} - r8n6{c6 c7} - r9c8{n6 n8} ==> r9c6 ≠ 8
naked-triplets-in-a-block: b8{r8c6 r9c5 r9c6}{n9 n6 n4} ==> r9c4 ≠ 9, r9c4 ≠ 6
whip[1]: b8n9{r9c6 .} ==> r1c6 ≠ 9
biv-chain[3]: r9n9{c2 c6} - c6n4{r9 r3} - r3n5{c6 c2} ==> r3c2 ≠ 9
hidden-pairs-in-a-row: r3{n7 n9}{c4 c8} ==> r3c4 ≠ 6
singles ==> r5c4 = 6, r5c6 = 8
biv-chain[4]: r1c8{n9 n3} - r6n3{c8 c2} - r7c2{n3 n7} - r9c2{n7 n9} ==> r1c2 ≠ 9
whip[1]: b1n9{r2c3 .} ==> r2c9 ≠ 9
singles ==> r2c9 = 4, r4c7 = 4
whip[1]: c9n9{r6 .} ==> r4c8 ≠ 9, r6c8 ≠ 9
biv-chain[3]: r2n9{c3 c1} - r2n6{c1 c6} - r8c6{n6 n9} ==> r8c3 ≠ 9
naked-single ==> r8c3 = 2
biv-chain-rc[4]: r2c6{n7 n6} - r8c6{n6 n9} - r8c1{n9 n3} - r7c2{n3 n7} ==> r7c6 ≠ 7
stte

Notice that, after the first whip[5], none of the patterns depends on the target(s) and almost all of them are very simple bivalue-chains (basics AICs).

[Leren]

I'm no expert on Hodoku. When I pasted the PM into it, the solution was shorter than the original puzzle, so AFAIK it takes all the missing candidates into account, but I could be wrong there, or there could be some option that I have not activated that might make it smarter. For the original puzzle Hodoku had one forcing chain :

Forcing Chain Contradiction in c3 => r1c6<>4 r1c6=4 r1c3<>4 r1c6=4 r3c56<>4 r3c9=4 r3c9<>2 r8c9=2 r8c9<>1 r8c4=1 r2c4<>1 r2c3=1 r2c3<>4r1c6=4 r7c6<>4 r7c1=4 r9c3<>4

that I think is a bit shorter . As I said, I'm no Hodoku expert. Maybe someone else can get it to work better.

Comparing your solution with Hodoku, I count 31 (non-single) moves for you and 27 for Hodoku, but they used two UR's, so maybe that is not a fair comparison. I tried to turn UR's off in Hodoku but for some reason it didn't work.

Leren

[denis_berthier]

Comparing your solution with Hodoku, I count 31 (non-single) moves for you and 27 for Hodoku, but they used two UR's, so maybe that is not a fair comparison. I tried to turn UR's off in Hodoku but for some reason it didn't work.

Even with the same set of rules, the number of moves strongly depends on many factors, such as the order they are applied. In particular, it is not stable under isomorphisms.

[Leren]

I suppose the main point is that the number of moves is "a lot" for those of us who are used to one or two trick moves to complete a puzzle.

I guess that's why no one else bothered. Of course I don't mean that to impugn your multi-move approach in any way. Keep it up.

Leren

[denis_berthier]

I've generated 1000 puzzles with this diagonals+centres pattern, ranging from SER 1.5 to 10.0.
I guess most of them will have a similar start and those with sufficiently low SER will be 1-step.

Here are the hardest two (SER 10.0 and 9.8):

Code: Select all

2.......8.3..2..1...6...4.....3.8....1..6..7....4.1.....4...6...7..9..3.8.......2 # 95550 FNBTHWXYKG C21.m/S8.f/M1.43.1 SER 10.0
1.......8.7..5..4...6...3.....7.6....4..9..2....2.5.....3...6...2..7..5.8.......1 # 92244 FNBTHWXYG C21.m/S8.f/M1.40.1  SER 9.8


It'd be interesting to see if the same covering technique can lower their ratings more than in the original puzzle.

If you want more of them, ask me.