The New Sudoku Players' Forum

by **StrmCkr** » Thu Nov 27, 2008 5:35 pm

ttt -you have to redesing the puzzle by removing the clue. in ss.

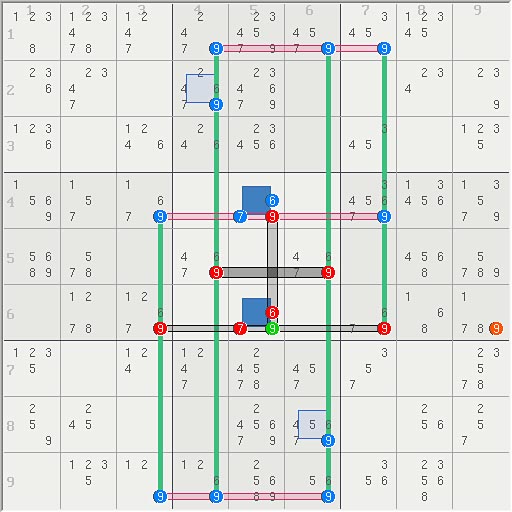
from there it leaves masive overlapped deadly patterns.
if you can spot them. you will see postions where the urs point out a positon that is a sinngle that are autoplaced even with out the given clue that was removed. ie hiddne in thed linked deadly patterns.

or they are expressed directly by sets of pairs that occur frequently at the same local with all possible subpuzzles.

or in some case the deadly patterns them selves give up a local that occurs often in all probable subpuzzle notations. ie. if the ur1.1 occurs there.(3 of 4 sells solve etc)

using uncompleted grids can show repeating patterns of occurances.
infernaces from there give additional clues how to solve.

thats how i see colin doing that...

it might also help if you had the program he uses to eliminated invalid clue from the beginnning...

problem with ss. is that in unvaldi grids you still must disable the "wrong" clue protection as it doesnt correctly display more then 1 valid subpuzzle.
it still trys to solve to 1 and disalows many valid moves.

colin your probly right on that one... i still have to go look at fm in depth more... mostly i was helping from other girds where i found the lil sk loop and allan mapped it out nicly.

problem is i make things very complicated...

i had two sk loops linked in tunsgton rod (one i found + normal one) and dropped it to singles basically in two move.

an overview.. basically if you remove a clue you are left with deadly patterns every where. if you disable them all or more importantly note where they are not. a single clue pattern is expressed by evaluating the potential solution counts.
(the same clues are given at specific locals due to other constraints)

basically the idea is that the same single clues are given from mutipoints of restrictions. if you remove some of those constraints others will still be there to express it as a singlton. basically your restricint the options and leaving non completed patterns which can be disabled as invalid.

by **champagne** » Thu Nov 27, 2008 9:56 pm

Hi ttt and strmckr,

tarek075 is clearly not easy, also cracked by my solver in a long and boring path.

I see your attempt to crack it thru our classical tools. Why not trying to catch Allan Barker point.

It seem to me that with symmetric diagrams, it is somehow possible.

Here was the diagram I produced

Code: Select all: 18 sets N45 N65 4679C3467 22 Linksets 4679B5 4R1347 6R3469 7R1467 9R1469 N24 N86 rank 4 7 triple points all linksets form N24 N86 4B5 4R4 4R1 4R3 4R7 <== 7 linksets | | | | | | | 4c7 ============= 447 417 437 | 4c3 ================= 413 433 473 4c6 | 486 456 ====== 416 436 | 7 triples points in sets N45 N65 4c4 424 | 454 ===== 414 434 474 V V V V | | | | N45 | | 445A 445A === 645B 645B =============745C 745C=========== 945D 945D | | | | | | | | | N65 | |=========== 665b | 665b==============765c ====765c ====== 965d= |= 965d | | | | | | | | | | 6c4 624 | ========== 654 ==|====|===|==634 | | | | | | 6c6 | 686 =============== 656 ==|===|===|== 696 | | | | | | 6c3 | | ==================== 643 663 633 | | | | | | 6c7 | | ==================== 647 667==|===697 | | | | | | | | | | | | | | | | | | | 7c4 724 | =================|====|===|===|===|== 754 | | 714 774 | | | 7c6 | 786 =================|====|===|===|===|== 756 | | 716 776 | | | 7c3 | | =================|====|===|===|===|====|===743 763 713 | | | | 7c7 | | =================|====|===|===|===|====|===746 766 | | | | | | | | | | | | | | | | | | | | 9c4 924 | =================|====|===|===|===|====|====|===|===|===|== 954 | | 914 994 9c6 986 =================|====|===|===|===|====|====|===|===|===|== 956 | | 916 996 9c3 =========================|====|===|===|===|====|====|===|===|===|== | 943 963 | 993 9c7 =========================|====|===|===|===|====|====|===|===|===|== | 947 967 917 | | | | | | | | | | | | | | | 15 linksets 6B5 6R4 6R6 6R3 6R9 7B5 7R4 7R6 7R1 7R7 9B5 9R4 9R6 9R1 9R9

Allan says it's not easy to apply the rules defining the regions and to establish rank 0 in such situations.

Let me try cutting first 2 of the three floors having 2 link sets. (supposed unoccupied in Allan method)

we come to that point

Code: Select all: 10 sets N45 N65 46C3467 12 Linksets 46B5 4R134 6R346 7R146 9R146 N24 N86 3 triple points all linksets form N24 N86 4B5 4R4 4R1 4R3 4R7 <== 7 linksets | | | | | | | 4c7 ============= 447 417 437 | 4c3 ================= 413 433 473 4c6 | 486 456 ====== 416 436 | 7 triples points in sets N45 N65 4c4 424 | 454 ===== 414 434 474 four seen as unoccupied | | | | N45 | | 445A 445A === 645B 645B =====//========745C == 945D | | | | N65 | |================ 665b 665b======//========765c == 965d= | | | | 6c4 624 | ============== 654====|===|==634 6c6 686 =============== 656 ==|===|===|== 696 6c3 ==================== 643 663 633 6c7 ==================== 647 667==|===697 | | | | | 5 linksets 6B5 6R4 6R6 6R3 6R9

Ths seem to be a global rank 2 situation that we could define as

original rank 4
four linksets suppressed => rank 0
but 2x2 triple poitns belonging to the same sets => rank 2 :?:

may be Allan will give a better explanation at that point

Let us try to cut now floor 4 as unoccupied

Code: Select all: N24 N86 | | | | N45 | | 445A =//== 645B 645B =====//========745C == 945D | | | | N65 | | =========== 665b | 665b======//========765c == 965d= | | | | 6c4 624 | =============== 654 ==|===|===|==634 6c6 686 =============== 656 ==|===|===|== 696 6c3 ==================== 643 663 633 6c7 ==================== 647 667==|===697 | | | | | 5 linksets 6B5 6R4 6R6 6R3 6R9

In that pattern sets N45 and N65 are now occupied in floor 6, if you cut known sets, you come to that situation

Code: Select all: N24 N86 6R3 6R9 | | 6c4 624 | =|==634 6c6 686 =|== 696 6c3 633 6c7 =====697

which seems to be the region in rank 0.

Due to global symmetry, there is not that much to do to cover all the field.

This seems relatively simple compare to other paths and leas to the first step:

r4c2 <> 2 r8c6 <>5

waiting now for Allan comments

champagne

by **champagne** » Sat Nov 29, 2008 3:09 am

Hi all,

I made a quick comparison between my standard process and Allan Barker model

Code: Select all: ........6..5..18...9...8.7....8.2.....3.1.2..4..5.3....6.....9...83..1..7.......4#tarx0075 1238 123478 1247 |2479 234579 4579 |3459 12345 6 236 2347 5 |24679 234679 1 |8 234 239 1236 9 1246 |246 23456 8 |345 7 1235 --------------------------------------------------------- 1569 157 1679 |8 4679 2 |345679 13456 13579 5689 578 3 |4679 1 4679 |2 4568 5789 4 1278 12679 |5 679 3 |679 168 1789 --------------------------------------------------------- 1235 6 124 |1247 24578 457 |357 9 23578 259 245 8 |3 245679 45679 |1 256 257 7 1235 129 |1269 25689 569 |356 23568 4

I summarize the sequence my solver got

2r8c2 5r8c6 6r5c1 5r5c8 8r5c8 2r2c4 6r2c4 4r1c2
4r3c5 4r1c8 5r8c9 4r3c4 5r7c6 3r1c7 7r5c9 7r8c6
7r1c4 7r7c9 3r2c1 7r4c9 6r3c3 6r4c1
7r1c5 9r6c9
7r6c9 7r7c7 7r8c5 2r8c9
1 r8c9=7 B

At that point, most of the print (310K) is covered.

If I apply Allan Barker model, I find the following eliminations:

2r4c2 5r8c6
4r1c28r3c4 6r6c8 7r1c25r6c2r7c9 9r6c9
2r6c3
1 r6c2=1

fist 2 lines seen and deeply studied before,

to ease the comparison, I sorted eliminations of my solver.

2r2c4 2r8c2 2r8c9
3r1c7 3r2c1
4r1c2 4r1c8 4r3c4 4r3c5
5r5c8 5r7c6 5r8c6 5r8c9
6r2c4 6r5c1 6r3c3 6r4c1
7r1c4 7r1c5 7r4c9 7r5c9 7r6c9 7r7c7 7r7c9 7r8c5 7r8c6
8r5c8
9r6c9

about half of the eliminations made following Allan model are missing in the solver path and the first assignment is very different.

Mixing both models should improve significantly the quality of the solution.

For the time being, the main drawback for Allan model is the time needed to extract the relevant Sets Linksets structures, but it's a new area to me.

champagne

by **Allan Barker** » Sat Nov 29, 2008 6:00 am

Rank 0 Question, tarek075

Champagne's 18 set initial loop:

Code: Select all: 18 sets N45 N65 4679C3467 22 Linksets 4679B5 4R1347 6R3469 7R1467 9R1469 N24 N86 rank 4

The question is why must the 2 linksets 2n4 and 8n6 always be occupied (rank 0) ? I think I have found a relatively simple layman's argument.

First, assume that all 4 layers are the same. The two central box cell sets 4N5, 6N5 contain one truth each, which must occupy two different layers because 4N5, 6N5 are connected at every layer by a central box 5 linkset.

Now look at the image for layer 9. It has 4 column sets with candidates in 7 rows (1245689) and is thus like a hidden AAALS. However, the cellset truth that occupies 9r5c6 (green) prevents (red) any of the 4 column truths from occupying r5 and r6. An occupied layer is therefore like an ALS. When 2 such ALS-like layers are connected through 2n4 and 8n6 they form an ALS loop, or rank 0. In simple terms, the only way to distribute the 8 column set truths must occupy 2n4 and 8n6.

Finally, only 2 of the 4 layers can be occupied but this will always occupy 2n4 and 8n6, which are therefore the only rank 0 linksets.

by **champagne** » Sat Nov 29, 2008 8:51 am

Hi Allan,

Too late to answer in the proper way to your post.

Some primary reactions you''ll find before I wake up.

1) Nice view to introduce a "dummy" '4' where it is missing in box 5. This gives a full symmetry to the diagram.

2) I guess your answer is correct. I was waiting for something more "academic".

Let me try one

In that ("now") fully symmetric diagram, you can cut any of three out the four digits floors (479 in my example).

I am convinced that the final status is "nodes/cells N2c4 n8c6 rank 0".

This comes out of the permutation analysis.

You are describing (subject to deeper analysis) how it can be focusing on floor '9'. The same is possible focusing on any floor.

I see 2 possibilities to justify the rank 0 region, all erasing floors:

a) Erasing a floor (2 triple points linkset form) each linkset has 2 triple points so you can not decrease rank by 2.You have to decrease it by one.

b) Assuming you have suppressed some triple points in a set, if you are adding more cuts in the same set, you can not account for more reduction in the count

c) If you cut triple points in such a way that all remainng candidates/nodes are occupied, then you can erase all occupied sets to find the remaining regions. If it is a set/link sets equilibrium, then it is rank 0.

The truth must somewhere in that area. :?:

BTW, I introduced some action in my prosess and I covered the full solution within your model.

Quick start as I said before, but very tough steps later and an overall process time 100 times higher than following my boring solution.

(All this subject to clearing bugs).

Still huge work to optimize the process

champagne

by **champagne** » Sat Nov 29, 2008 11:40 pm

Hi Allan,

Let me try again a more precise way to come to the conclusion just thinking about triple points.

After having thought what could be the specificity of my diagram (and of your first loop in Fata Morgana as well), I came to the conclusion that it starts from the fact that 2 triple points linkset form are attached to the same linkset (Box 5 sets for 679, extended to 4 if we add your "dummy").

When 2 triple points are attached to the same linkset, only 2 possibilities have to be considered :

. One triple point occupied
. No triple point occupied.

So in fact, (what I had seen) when you cut one floor, rank is decreased by one and not by 2.

you can cut in that way 2 of the four floors. You come to a situation globally rank2 .

Here is the second specificity with now two sets N45 N65 reduced to 2 triple points each,
.one of them must be valid in each set.
.eah box5 linkset will be occupied.

We are in that position in my diagram.

Code: Select all: 10 sets N45 N65 46C3467 12 Linksets 46B5 4R134 6R346 7R146 9R146 N24 N86 3 triple points all linksets form N24 N86 4B5 4R4 4R1 4R3 4R7 <== 7 linksets | | | | | | | 4c7 ============= 447 417 437 | 4c3 ================= 413 433 473 4c6 | 486 456 ====== 416 436 | 7 triples points in sets N45 N65 4c4 424 | 454 ===== 414 434 474 four seen as unoccupied | | | | N45 | | 445A 445A === 645B 645B =====//========745C == 945D | | | | N65 | |================ 665b 665b======//========765c == 965d= | | | | 6c4 624 | ============== 654====|===|==634 6c6 686 =============== 656 ==|===|===|== 696 6c3 ==================== 643 663 633 6c7 ==================== 647 667==|===697 | | | | | 5 linksets 6B5 6R4 6R6 6R3 6R9

Only one possibility in that rank 2 region : 665 occupied, 445 occupied

Erasing sets where the candidate is known lead to the region rank 0 as below.

Code: Select all: N24 N86 4R1 4R3 4R7 | | | | | 4c7 ============= 417 437 | 4c3 ================= 413 433 473 4c6 | 486 ====== 416 436 | 4c4 424 | ===== 414 434 474 6c4 624 | =============================634 6c6 686 ==============================|== 696 6c3 ==================== 663 633 6c7 ==================== 667==|===697 | | | 6R6 6R3 6R9

Whatever is the way you combine reduction fo the number of floors, N24 and N86 are always in the rank 0 subregion.

I feel much more confortable with such an explanation which is 100% sets/link sets application. I hope you will agree on that

champagne

by **champagne** » Sun Nov 30, 2008 4:13 am

Hi all,

Turning around Allan model, I think I got an easy explanation for the elimination of 2n2c4 and 5n8c6.

The start is all super candidates filling N45 and N65.
Six possibilities. 4&6 4&7 4&9 6&7 6&9.

Here is a diagram of the situation starting from N45;N65 filled by 4&9.

Code: Select all: 1238 123478 1247 |2479 234579 4579 |3459 12345 6 236 2347 5 |24679 234679 1 |8 234 239 1236 9 1246 |246 23456 8 |345 7 1235 --------------------------------------------------------- 1569 157 1679 |8 4 2 |35679 13456 13579 5689 578 3 |67 1 67 |2 4568 5789 4 1278 12679 |5 9 3 |679 168 1789 --------------------------------------------------------- 1235 6 124 |1247 24578 457 |357 9 23578 259 245 8 |3 245679 45679 |1 256 257 7 1235 129 |1269 25689 569 |356 23568 4

Code: Select all: N24 N86 4R1 4R3 4R7 | | x x x 4c7 ========417 437 | 4c3 =======413 433 473 4c6 | 486 416 436 | 4c4 424 | 414 434 474 9c4 924 | ========== = 914 994 9c6 986 =========== 916 996 9c3 =================== 943 | 993 9c7 =================== 947 917 x x x 9R4 9R1 9R9 extra candidates in raws play no role.

if(424 and 486) are False, we have a deadly pattern in floor 4
if(924 and 926) are Flase, we have a deadly pattern in floor 9.

Must have one of each. N24 and N86 are filled.

Same using any valid super candidate for N45;N56.

This is a quasi transcription of Allan Sets/ Link sets analysis

champagne

by **Allan Barker** » Sun Nov 30, 2008 4:31 am

Champagne, here is the headache you requested.

This is the official academic rank argument for this kind of loop,
0) The raw rank is linksets - basesets = 4.
1) Two triplets (and thus 4 linksets) must always be occupied thus the overall rank of the whole structure, anywhere cannot be more than 2.
2) The 2 occupied triplets can be anywhere but must be in two different layers.
3) Remember: unoccupied triplets lower the rank in the direction of their "strong-set" leg.
4) Thus, linksets on un-occupied floors will have a lower rank until a point of convergence (this is the hard part), including 2n4 and 8n6.
5) The real observable rank is always the worst case (highest) of different configurations. Since 2n4 and 8n6 are always in a lower rank region, they are rank 0. The linksets in the floors will not always be in a lower lank region therefore their rank is higher (actually they are rank 1, by measurement).

I have left out some of the tedious detail to keep it clean, so this would not be a proof. The proof would be the same but tedious. I do a lot of work to confirm such ideas before believing them.

If this picture is true, it predicts that:
1) 3 or more layers will all behave the same, i.e., only 2 rank 0 linksets, and
2) a two layer example will be completely rank 0 everywhere.

This you can confirm by using two layers, but you must also remove the extra (other layer) candidates from 46N5 to make the model work.

Whew. I have not yet finished studying your argument but it will be interesting to compare. There is also a strong relation between rank regions and rectangular sub regions in pigeon hole matrices.

I now have a collection of 6 different of loops that produce the same rank in different ways. These include loops with and with out the 46N5 sets, some with box 5 linksets, some with box 5 sets, and some with no box 5 sets linksets. I will try to post them somewhere soon, maybe on my website.

by **champagne** » Sun Nov 30, 2008 6:07 am

Allan Barker wrote:0) The raw rank is linksets - basesets = 4.
1) Two triplets (and thus 4 linksets) must always be occupied thus the overall rank of the whole structure, anywhere cannot be more than 2.
2) The 2 occupied triplets can be anywhere but must be in two different layers.
3) Remember: unoccupied triplets lower the rank in the direction of their "strong-set" leg.
4) Thus, linksets on un-occupied floors will have a lower rank until a point of convergence (this is the hard part), including 2n4 and 8n6.
5) The real observable rank is always the worst case (highest) of different configurations. Since 2n4 and 8n6 are always in a lower rank region, they are rank 0. The linksets in the floors will not always be in a lower lank region therefore their rank is higher (actually they are rank 1, by measurement).

0) and 2) no problem.

1) I guess this means that 2 triplets occupied is equivalent to lowering the linksets count by 2. This is not 100% clear to me.

Points 3) 4) 5) are coherent with my statements.

BTW, I made a full exploration of that puzzle. After a "relatively easy" start, I find terrible situations with necessity to combine five floors and huges SLG.

Did you try to solve it entirely :?:

champagne

by **Allan Barker** » Sun Nov 30, 2008 4:37 pm

Champagne wrote:I guess this means that 2 triplets occupied is equivalent to lowering the linksets count by 2. This is not 100% clear to me.

The heart of the rank concept is, how many linksets (cover sets) must I choose to guarantee that at least one has a truth? With 12 linksets and 10 truths, the answer is clearly 3 (rank 2). If however, at least one triplet (any one) is always occupied (occupying 2 linksets) the answer is 2 (rank1).

Point 3) is the other basic point about triplets. if occupied the global rank must be lower, if un-occupied the local set-branch rank must be lower, because it is now "covered" by 1 less cover set. In summary, the upper branch must always be lower.

Here in lies the shift from implication reasoning to a static global picture. There is a small but real similarity to arguments used in statistical thermodynamics, which also derives static global properties from arguments based on permutation states.

Champagne wrote:BTW, I made a full exploration of that puzzle. After a "relatively easy" start, I find terrible situations with necessity to combine five floors and huges SLG.
Did you try to solve it entirely

I gave up! I had the same experience, after several eliminations, it became clear that solving the puzzle would be a slow, tedious process. I still solve puzzles step by step by hand.

Note that Fata Morgana is just the opposite, after the initial-loops, it solves quite easily.

This one needs a name, a dark and sinister name.
.

by **ttt** » Sun Nov 30, 2008 9:33 pm

Hi All,
As reference on other view for tarx0075.

Code: Select all: *-----------------------------------------------------------------------------* | 1238 123478 12(47) | 2479 234579 4579 | 35(49) 12345 6 | | 23(6) 23(47) 5 | 2(4679) 23(4679)1 | 8 23(4) 23(9) | | 1236 9 12(46) | 246 23456 8 | 3(4)5 7 1235 | |-------------------------+-------------------------+-------------------------| | 1569 157 1(679) | 8 4679 2 | 35(4679)13456 13579 | | 5689 578 3 | 4679 1 4679 | 2 4568 5789 | | 4 1278 12(679) | 5 679 3 | (679) 168 1789 | |-------------------------+-------------------------+-------------------------| | 1235 6 12(4) | 1247 24578 457 | 35(7) 9 23578 | | 25(9) 2(4)5 8 | 3 25(4679)5(4679) | 1 25(6) 25(7) | | 7 1235 12(9) | 1269 25689 569 | 35(6) 23568 4 | *-----------------------------------------------------------------------------*

My view based on Steve’s concept for SK loop, consider box 4:

Code: Select all: 1- If SK loop => (679)r46c3 => pair (18)r6c89 => r6c9<>9 2- If "nearly SK loop" => C01: at least one of 6’s, 7’s, 9’s must be true on r46c3 C02: box 1 contain (467) at r2c12/r13c3 => r1c2<>47, r3c1<>6 C03: box 2 contain at least two of 4’s, 6’s, 7’s, 9’s => r2c45<>23 C04: box 3 contain (49) at r2c78/r13c7 => r1c8<>4 C05: box 6 contain at least two of 4’s, 6’s, 7’s, 9’s => r4c7<>35 C06: box 8 contain at least two of 4’s, 6’s, 7’s, 9’s => r8c56<>25 C07: box 9 contain (67) at r79c7/r8c89 => r7c9<>7, r9c8<>6 C08: C03&C06 => quad(4679)r2468c5 => r1379c5<>4679 C09: C02&C08 => (X-wing 4’s r28c25)=(4)r4c5-(4)r4c7=(4)r13c7 => r2c8<>4 C10: C04-C05-C09 => r4c7<>4, (679)r46c7 a/ If 6’s at r46c3, C02 => r2c1=6 => r3c4=6 => r5c14<>6 => either r5c6=6 or r5c8=6 then r46c7<>6 and C10 => pair(79)r46c7 => r6c9<>9 b/ If 7’s at r46c3, C02-C07-C08 => (r1c23, r17c5, r7c9, r5c2)<>7 => (X-wing 7’s r15c46)=(7)r5c9-(7)r8c9=(7)r8c56 => r7c46<>7, r7c7=7 and C10 => pair(69)r46c7 => r6c9<>9 c/ If 9’s at r46c3, C08 => (r5c1, r19c5,r9c3)<>9 => (X-wing 9’s r59c46)=(9)r5c9-(9)r2c9=(9)r1c7 => r1c46<>9, r1c7=9 => r2c9<>9 and C09 => pair(23)r2c89 => r2c1=6 => r3c3<>6 => triple(124)r379c3 => r46c3<>12 => pair(18)r6c89 => r6c9<>9

conclusion: r6c9<>9

Presenting as diagram is too complex and based on above if we extend chains then can eliminate some more (as r6c8<>6, r6c3<>1) but…

ttt

by **ttt** » Fri Jan 02, 2009 2:44 am

Hi All,
I was drunk so much…. (…Vodka…)
Not much things to considerate… recently...

champagne: symmetries... I think that you should not considerate that much...

ttt

by **champagne** » Fri Jan 02, 2009 3:58 am

ttt wrote:
champagne: symmetries... I think that you should not considerate that much...

ttt

I can understand your POV, it is quite special. For me it is nearly behind me.

Nevertheless, I found some fun in finding and coding the most common pattern.

I am mainly working on AUR and insertion of the typical pattern seen in Fata Morgane Tarx0075 Golden Nugget . . . in AIC's.

Hope to come with new solving capabilities end of this month, much closer to what yo can achieve.

champagne

by **ttt** » Fri Jan 02, 2009 4:16 am

champagne wrote:I am mainly working on AUR and insertion of the typical pattern seen in Fata Morgane Tarx0075 Golden Nugget . . . in AIC's.
Hope to come with new solving capabilities end of this month, much closer to what yo can achieve.

For FM, we finished it so I think that we'll try on tarx0075 & GN (at least for me...

)

Edit: wow... I'm 99, long time... and I missed ravel....

ttt

by **ttt** » Thu Jan 22, 2009 3:44 pm

Hi All.
Suexratt hardest puzzle here: tarx0134

Code: Select all: ........8..3...4...9..2..6.....79.......612...6.5.2.7...8...5...1.....2.4.5.....3 *--------------------------------------------------------------------------------------* | 12567 2457 12467 | 134679 13459 34567 | 1379 1359 8 | | 15678 578 3 | 16789 1589 5678 | 4 159 2 | | 1578 9 147 | 13478 2 34578 | 137 6 157 | |----------------------------+----------------------------+----------------------------| | 12358 23458 124 | 348 7 9 | 1368 13458 1456 | | 35789 34578 479 | 348 6 1 | 2 34589 459 | | 1389 6 149 | 5 348 2 | 1389 7 149 | |----------------------------+----------------------------+----------------------------| | 23679 237 8 | 1234679 1349 3467 | 5 149 14679 | | 3679 1 679 | 346789 34589 345678 | 6789 2 4679 | | 4 27 5 | 126789 189 678 | 16789 189 3 | *--------------------------------------------------------------------------------------*

Move 1: present as diagram => r6c5 & r1378c4<>4

Code: Select all: (3)r6c5-(3=hp48)r45c4* || (3)r6c1---(3)r78c1=(3)r7c2-(3)r7c456 || | || || --(3)r6c5=(3)r45c4-(3)r8c4 || | || || | (hp35)r8c56-(8)r8c56 || | || || | (8)r8c4-(8=hp34)r45c4* || | || || | (8)r8c7-(8)r6c7 || | || || ---------------------------------------(8)r6c1 || || || (8)r6c5-(8=hp34)r45c4* || (3)r6c7---(3)r13c7=(3)r1c8-(3)r1c456 | || --(3)r6c5=(3)r45c4-(3)r3c4 | || | (3)r3c6-(8)r3c6 | || | (8)r3c4-(8=hp34)r45c4* | || | (8)r3c1-(8)r6c1 | || -----------------------------------(8)r6c7 || (8)r6c5-(8=hp34)r45c4*

The grid after above move.

Code: Select all: *-----------------------------------------------------------------------------* | 12567 2457 12467 | 13679 13459 34567 | 1379 1359 8 | | 15678 578 3 | 16789 1589 5678 | 4 159 2 | | 1578 9 147 | 1378 2 34578 | 137 6 157 | |-------------------------+-------------------------+-------------------------| | 12358 23458 124 | 348 7 9 | 1368 13458 1456 | | 35789 34578 479 | 348 6 1 | 2 34589 459 | | 1389 6 149 | 5 38 2 | 1389 7 149 | |-------------------------+-------------------------+-------------------------| | 23679 237 8 | 123679 1349 3467 | 5 149 14679 | | 3679 1 679 | 36789 34589 345678 | 6789 2 4679 | | 4 27 5 | 126789 189 678 | 16789 189 3 | *-----------------------------------------------------------------------------*

Move 2: present as diagram => r6c5 & r2389c4<>8, single r6c5=3

Code: Select all: AUR(34)r45c24 || (8)r45c4* || (4)r1c2-(4)r1c56=(4)r3c6-(3)r3c6 || || || (3)r3c4-(3=hp48)r45c4* || || || (3)r3c7--(3)r1c8=AUR(34)r45c48 || | || || | (8)r45c4 || | || || | (4)r7c8-(4)r8c9=(hp45)r8c56-(3)r8c56 || | || || | (3)r8c4-(3=hp48)r45c4* || | || || | (3)r8c1-(3)r6c1 || | || || ---------------------------------------------(3)r6c7 || || || (3)r6c5-(3=hp48)r45c4* || (3)r7c2—----(3)r7c6 | || | (3)r8c6--(hp45)r8c56=(4)r8c9-(4)r7c8=AUR(34)r45c48 | || | || | || | (8)r45c4* | || | || | || | (3)r1c8-(3)r1c456 | || | || | || -------------------------------------(3)r3c6 | || || | || (3)r3c4-(3=hp48)r45c4* | (3)r1c6-(3)r1c8-AUR(34)r45c48 | || || | || (8)r45c4* | || || | || (4)r7c8-(4)r8c9=(45)r8c56-------------------- | || | | || | | (3)r3c6-(4)r3c6=(4)r3c3-(4)r6c3=(4)r6c9-(4)r8c9=(hp45)r8c56-(3)r8c56 | || ----------------------------------------------------------------(3)r8c1 || (3)r8c4-(3=hp48)r45c4*

After two moves above the puzzle is still hard but not hardest…

BTW, I don't see this puzzle on champagne's BB list

Edit: I don't know how to reduce size for diagram of move 2... :!:

ttt

The New Sudoku Players' Forum

AIC's net equivalent to forcing net