The New Sudoku Players' Forum

[Glyn]

eleven Apart from the typo you mention I have no problem except the weak link between (1)r9c5-(6)r8c5. Maybe ttt can clear that one up.

[ttt]

I am impressed by your use of AUR patterns.

Thanks and hope it’s useful for you

If (second diagram) the typo is, that (6)r6c56 should be (6)r5c46, i still cant see, how the case
(1)r1c5, (1)r6c8, (3)r9c8, (1)r7c1, (1)r4c2 is handled.
Sorry, i have no practice with these diagrams, i'm just guessing what it means.

Thanks, I edited.
Above diagram meant (second diagram for example): first, consider 1’s on col.5

Code: Select all

1-If r46c5=1 => pair (36)r5c46 => r5c238<>6

2-If r1c5=1 => r1c8<>1, consider 1’s on col.8 =>
a/If r5c8=1 => pair (36)r5c46 => r5c238<>6
b/If r6c8=1 => r6c8<>3 => r9c3=3 => r9c5 & r7c7<>3 => r4c2<>1 and to avoid UR(13)r57c46 => either r5c46=6 => r5c238<>6 or r7c1=1 => r9c2<>1, consider 1’s on col.2 => r5c2=1 => pair (36)r5c46 => r5c238<>6 

3-If r9c5=1 => r4c2 & r9c2<>1, r5c2=1 => pair (36)r5c46 => r5c238<>6

I’m not sure, above explanations is enough & clearly, sorry about that.

I have no problem except the weak link between (1)r9c5-(6)r8c5. Maybe ttt can clear that one up.

Thanks for shown that wrong, I edited (I’m in a jumble between 3’s & 6’s).

ttt

[eleven]

This is the case i meant:

b/If r6c8=1 => r6c8<>3 => r9c3=3 => r9c5 & r7c7<>3 => r4c2<>1 and to avoid UR(13)r57c46 => either r5c46=6 => r5c238<>6 or r7c1=1 => r9c2<>1, consider 1’s on col.2 => r5c2=1 => pair (36)r5c46 => r5c238<>6

r9c2<>1 does not imply r5c2=1 in this grid, because there is a 1 in r4c2 either.
[Added:] But i saw now, that r4c2=1 implies r5c46<>3 via the finned x-wing for 3 in c25, so it also works in this case.

[ttt]

This is the case i meant:

b/If r6c8=1 => r6c8<>3 => r9c3=3 => r9c5 & r7c7<>3 => r4c2<>1 and to avoid UR(13)r57c46 => either r5c46=6 => r5c238<>6 or r7c1=1 => r9c2<>1, consider 1’s on col.2 => r5c2=1 => pair (36)r5c46 => r5c238<>6

r9c2<>1 does not imply r5c2=1 in this grid, because there is a 1 in r4c2 either.
[Added:] But i saw now, that r4c2=1 implies r5c46<>3 via the finned x-wing for 3 in c25, so it also works in this case.

Hope below is more detail:

Code: Select all

b/If r6c8=1
=>r6c8<>3 =>r9c8=3 =>r7c7<>3 and to avoid UR(13)r57c46 =>r5c46=6 or r7c1=1 =>r9c2<>1(*)   
                   =>r9c5<>3 =>r2c5=3 =>r2c2<>3 =>r4c2=3 =>r4c2<>1(**)

(*)&(**) => on column2: r5c2=1

ttt

[eleven]

Ok, thanks, i looked at the grid, where the 3's were not eliminated from the first move.

[champagne]

Hi ttt,

I made small changes in your diagram showing r5c278<>3.
I express the same fact as # X=(1&6)r5c46
and I try to avoid using AUR.

Code: Select all

 +   ..6+ ..6+ | 1.6+ 1.6+ 1.6+ | ...+ 1..+  -
.3.+ .3.+   -  | .3.+ .3.+  -   |  -     +   +
.3.+   -  ..6+ | 136+  -   136+ |  +     -  1..+
------------------------------------------------
1.3+ 136+ ..6+ | 136+ 136+  -   | .3.+   -  1.6+
 -   136+ ..6+ | 136   -   136  | .3.+ 136+  -
13.+  -   ..6+ |  -   136+  -   | .3.+ 136  1.6+
------------------------------------------------
1..+  -    +   | 136+  -   136+ | .3.+  -   ..6+
 +    +    -   |  -   ..6+ ..6+ |  -   ..6+ ..6+
 -   1..+  +   | 13.+ 13.+ 13.+ | .3.+ .3.+   +

# X=(1&6)r5c46

Code: Select all

 1)r1c5-(1)r1c8
 ||  |   ||
 ||  |  (1)r5c8- X
 ||  |   ||
 ||  |  (1)r6c8-(6)r6c8
 ||  |           ||
 ||   \         (6)r5c8- X
 ||    \         ||
 ||     \        ||                                 
 ||      \_      (6)r8c8 --(6)r8c5     
 ||         \               ||         
 (1)r46c5-X  \__________   (6)r46c5- X
 ||                      \  ||             
 ||               (6)r1c2-(6)r1c5
 ||                ||
 ||               (6)r5c2- X
 ||                ||
 ||       (1)r4c2-(6)r4c2
 ||        ||
 ||        (1)r5c2-X
 ||        ||
(1)r9c5---(1)r9c2     

I hope this is correct.
My next question is

should my solver find it and if yes why did he not??

That's my next task.

EDIT:

As such, this diagram dit not conclude.
I added one missing weak link 1r1c5 - 6r1c5, but it is not yet enough..

[ttt]

I added one missing weak link 1r1c5 - 6r1c5, but it is not yet enough..

Yes, I think that the using UR is short way to conclude r5c278<>3

ttt

[champagne]

I added one missing weak link 1r1c5 - 6r1c5, but it is not yet enough..

Yes, I think that the using UR is short way to conclude r5c278<>3

ttt

We can conclude easily also with my diagram, but it uses another UR r35c46, this is not what I was looking for.

Code: Select all

(1)r46c5-X 
 ||                         
 ||    (1)r6c8-(6)r6c8
 ||      ||       ||
 ||  X-(1)r5c8  (6)r5c8- X
 ||      ||       ||
 ||    (1)r1c8    ||                 <=>(1)r1c8
 ||      |      (6)r8c8 --(6)r8c5          |
 ||      |                  ||           1r1c456
 ||     /                 (6)r46c5- X      ||
 ||    /                    ||           1r3c46
(1)r1c5   --------       (6)r1c5         UR16 r35c4
 ||                     /                |
 ||              (6)r1c2 -- 6r1c456 = 6r3c46
 ||                ||
 ||               (6)r5c2- X
 ||                ||
 ||       (1)r4c2-(6)r4c2
 ||        ||
 ||        (1)r5c2-X
 ||        ||
(1)r9c5---(1)r9c2     

Now both possibilities of the central nice loop after (1&6)r5c46 are shown not valid.

I think more and more I have to include some UR deadly patterns in my lay-out.

[ttt]

Hi All,

Code: Select all

*-----------* 
 |...|...|..6|
 |..5|..1|8..|
 |.9.|..8|.7.|
 |---+---+---|
 |...|8.2|...|
 |..3|.1.|2..|
 |4..|5.3|...|
 |---+---+---|
 |.6.|...|.9.|
 |..8|3..|1..|
 |7..|...|..4|
 *-----------*

 *-----------------------------------------------------------------------------*
 | 1238    123478  124(7)  | 2479    234579  4579    | 345(9)  12345   6       |
 | 23(6)   234(7)  5       | 24(679) 234(679)1       | 8       234     23(9)   |
 | 1236    9       124(6)  | 246     23456   8       | 345     7       1235    |
 |-------------------------+-------------------------+-------------------------|
 | 1569    157     1(679)  | 8       4679    2       | 345(679)13456   13579   |
 | 5689    578     3       | 4679    1       4679    | 2       4568    5789    |
 | 4       1278    12(679) | 5       679     3       | (679)   168     1789    |
 |-------------------------+-------------------------+-------------------------|
 | 1235    6       124     | 1247    24578   457     | 35(7)   9       23578   |
 | 25(9)   245     8       | 3       245(679)45(679) | 1       25(6)   25(7)   |
 | 7       1235    12(9)   | 1269    25689   569     | 35(6)   23568   4       |
 *-----------------------------------------------------------------------------*

I’m studying this puzzle (tarx0075 from http://forum.enjoysudoku.com/viewtopic.php?t=4212&start=930) and found r2c4<>24 & r2c5<>234 that consider UR[(67),(69),(79)]r46c37, but the presenting by diagram is too complex…
Do you have any idea for this?

Thanks to all,
ttt

[champagne]

Hi ttt,

No evidence of symmetry effects, but let's Merlin talk about it.

I am not expert in Allan method handling, but studying floors, it comes than you can find something using floors 4679.
No surprise if you have a look to box 5.

Code: Select all

1238 123478 1247  |2479  234579 4579  |3459   12345 6     
236  2347   5     |24679 234679 1     |8      234   239   
1236 9      1246  |246   23456  8     |345    7     1235 
---------------------------------------------------------
1569 157    1679  |8     4679   2     |345679 13456 13579
5689 578    3     |4679  1      4679  |2      4568  5789 
4    1278   12679 |5     679    3     |679    168   1789 
---------------------------------------------------------
1235 6      124   |1247  24578  457   |357    9     23578
259  245    8     |3     245679 45679 |1      256   257   
7    1235   129   |1269  25689  569   |356    23568 4

Possible eliminations should be the following

4: r1c28 r3c4
6: r6c8
7: r1c25 r6c2 r7c9
9: r6c9
and 2 in cell r2c4; 6 in cell r8c6.

One possible clue: whatever is the couple used in r5c46 (4&6 4&7 4&9 6&7 6&9 7&9), r2c4 and r8c6 have one of the values 4679.

My solver proposes something complex, but I'll check if he delivers information than can help here. (r5c46 is an AC2 studied by the solver)

This puzzle is ranked by my solver close to the hardest.

We can see also than other eliminations are not in row 5.

champagne

[ttt]

Hi champagne,
Thanks for your informations!

One possible clue: whatever is the couple used in r5c46 (4&6 4&7 4&9 6&7 6&9 7&9), r2c4 and r8c6 have one of the values 4679.

Yes, I was thinking this but it look quite complex to present as diagram then I changed to others path. I’ll try again…

No evidence of symmetry effects, but let's Merlin talk about it.

Yes, I’m also studying Merlin’s ways to know how he can defeat Morgan…

ttt

[champagne]

Hi champagne,
Thanks for your informations!

One possible clue: whatever is the couple used in r5c46 (4&6 4&7 4&9 6&7 6&9 7&9), r2c4 and r8c6 have one of the values 4679.

Yes, I was thinking this but it look quite complex to present as diagram then I changed to others path. I’ll try again…

I am convinced this will be the easiest way for Allan, but wait and see. As you know, all we are doing (except using uniqueness) has an equivalence in Allan model, reverse is not granted. That's why I work hard on it.

This gives me no more time to work on Merlin's method, but it will come later.

I am far from being convinced it can be added to what is already in my solver if symmetry does not appear clearly. But we will see.

May be meantime we will be linked to some detailed explanations at the level of non native english speakers

[Allan Barker]

I am convinced this will be the easiest way for Allan, but wait and see.

This is a really difficult puzzle, all the way, however after some searching, I think I found the "initial loop". It's easier to understand after Fata Morgana.

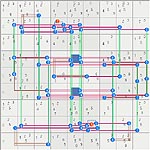
FM first loop summary . The first FM loop had 2 central-box strong cell-sets surrounded by 3 identical layers, one of the layers was anti-symmetric wrt the other two. The anti-symmetry was required (for that logical design) to cause the elimination. Making all 3 layers the same prevented the eliminations.

This puzzle's initial loop is similar (same family) but larger with more complex symmetry. It has 4 layers and only the bottom 3 are the same. Among the bottom 3 layers there are 3 different symmetries, reflecting the symmetry of the puzzle. The top layer, layer 4, also has a broken symmetry in the puzzle.

Studying the symmetry of the assigned cells could help a solver find such loops, since they have the same symmetry

So far there are two styles, first type (shown here):

Layer 4 diff. 3 row sets
Layer 6 same 2 rows, 1 column, 1 box -normal-
Layer 7 same 2 rows, 1 column, 1 box -rotation-
Layer 9 same 2 rows, 1 column, 1 box -reflection-

Second type:

Layer 4 diff. 3 row sets
Layer 6 same 2 rows, 2 column -normal-
Layer 7 same 2 rows, 2 column -normal-
Layer 9 same 2 rows, 2 column -reflection-
The common property seems to be large, symmetrical, layered, loopish structures that eliminate their candidates by rank 0 linksets (cover sets), like continuous nice loops. Not all linksets need be rank 0. The other property is they only appear in the initial part of the solution path. I also placed this in the monster loop thread, and will add to it there.

Code: Select all

  +-----------------------------------------------------------------------------+
  | 1238    123478  124(7)  | 2479    234579  4579    | 3459    12345   6       |
  | 23(6)   23(47)  5       | 2(4679) 23(4679 1       | 8       23(4)   23(9)   |
  | 1236    9       1246    | 246     23456   8       | 345     7       1235    |
  +-----------------------------------------------------------------------------+
  | 159(6)  157     1(679)  | 8       (4679)  2       | 345(679 13456   135(79) |
  | 589(6)  578     3       | 679(4)  1       679(4)  | 2       568(4)  58(79)  |
  | 4       1278    12(679) | 5       (679)   3       | (679)   168     18(79)  |
  +-----------------------------------------------------------------------------+
  | 1235    6       124     | 1247    24578   457     | 357     9       23578   |
  | 25(9)   25(4)   8       | 3       25(4679 5(4679) | 1       25(6)   25(7)   |
  | 7       1235    12(9)   | 1269    25689   569     | 35(6)   23568   4       |
  +-----------------------------------------------------------------------------+

Set Elimination Logic:

Code: Select all

RABX 58 Nodes, Raw Rank = 5 (linksets - sets)
     17 Sets =  {4679r2 4r5 4679r8 79c3 6c7 46n5 6b4 79b6}
     22 Links = {679r4 679r6 6c1 4c2 4679c5 4c8 79c9 2n4 8n6 7b1 4b5 39b7 6b9}
     --> (2n4) => r2c4<>2, (8n6) => r8c6<>5

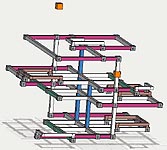
Thumbs to images: left: 2D grid images, right 3D jiggle pic.
(the right 3D image is meant to jiggle to give a sense of depth)


.
Set Logic Diagram and other examples here in Great Monster Loops

[champagne]

Hi,

After Allan has produced his SLG diagram, I compared to the proposal of my solver.
Different as usual.

I propose it because it seems to me there are interesting things in it.

Code: Select all

1238 123478 1247  |2479  234579 4579  |3459   12345 6     
236  2347   5     |24679 234679 1     |8      234   239   
1236 9      1246  |246   23456  8     |345    7     1235 
---------------------------------------------------------
1569 157    1679  |8     4679   2     |345679 13456 13579
5689 578    3     |4679  1      4679  |2      4568  5789 
4    1278   12679 |5     679    3     |679    168   1789 
---------------------------------------------------------
1235 6      124   |1247  24578  457   |357    9     23578
259  245    8     |3     245679 45679 |1      256   257   
7    1235   129   |1269  25689  569   |356    23568 4   

I searched a limited group of sets eliminating 2r2c4 and 5r8c6.
I got this group as minimum.

Code: Select all

N:...............................X.................X.X.............................
R:...........................X.XX..X.............XX.X..XX..X.XX...........X..X....X
C:.............................XX.XX.............XX.XX....XX.XX.............XX.XX..
B:...............................X.................X........X......................
  1        2        3        4        5        6        7        8        9       
=37 sets  and likely some of theese used as well
NV.xxxxxx...x.xx......xxx....x.x.x.xxxx..x.x.xx..x.x.x.x...xxx.......xx......xxx...
  1        2        3        4        5        6        7        8        9       

Here, we have a full symmetry in columns. Only 467B7 are in on the boxes side.
No set in rows 2;5;8 As in Allan loop, the key cells/nodes are N45 and N65.

I made an attempt to build the corresponding diagram

Code: Select all

N45         445A  445A            645B 645B             745C 745C               945D 945D
N65                               665b     665b         765c     765c           965d    965d
                                    |                     |                       |
4c7               447  417 437      |                     |                       |           
4c3                    413 433 473  |                     |                       |
4c6     486 456        416 436      |                     |                       |
4c4 424     454        414 434 474  |                     |                       |
                                    |                     |                       |
6c4 624                            654          634       |                       |
6c6     686                        656              696   |                       |
6c3                                    643 663  633       |                       |
6c7                                    647 667      697   |                       |   
                                                          |                       |
7c4 724                                                  745          714  774    |           
7c6     786                                              756          716  776    |
7c3                                                           743 763 713         | 
7c7                                                           746 766             |   
                                                                                  |
9c4 924                                                                          954         914  994
9c6     986                                                                      956         916  996
9c3                                                                                  943 963      993
9c7                                                                                  947 967 917


This is not exatly the proposal of my program. I added 9b5 and 9r5. Reversely, I suppressed cell/node N67, but it should still be valid.

We have 18 sets and 22 linksets in that construction, and 7 triples, all linksets form.



I hope Allan can make a SLG out of it, but I am sure this is enough to eliminate the 2 candidates of the target if we stick to the solver proposal..
I tried to find something in the form of forcing net, but I gave up, nothing simple came.

champagne

[ttt]

Hi Allan & champagne,

I consider this:
1- Look r2c45 with candidates 4,6,7,9 => at least TWO of [(6)r1c2, (4)r2c2, (7)r2c2, (4)r2c8, (9)r2c9] must be true – Group 1.
2- Look r8c56 with candidates 4,6,7,9 => at least TWO of [(9)r8c1, (4)r8c2, (6)r8c8, (7)r8c9] must be true – Group 2.

From above we can eliminate at least two candidates: r46c3<>1, presenting as diagram for this is not too complex but not nice then I’m still thinking more…

ttt