The New Sudoku Players' Forum

by **Allan Barker** » Thu Nov 20, 2008 2:40 am

Hi Champagne,

Maybe you need to re-check this set group. Below are the sets I read in and an image. In the grid image, all (red) rows and many (green) columns have some candidates only covered by one set. These must become linksets. However, they are arranged in a way that much of the pattern cannot not be covered by strong sets. Also, the number of permutations is over 8000000 but should be about 2000.

However, the number of sets, the shape, and the 2 center box 'N' sets all look good, maybe it is something simple.

Code: Select all: EABX 88 Nodes, 37 Sets = {4r1347 6r3469 7r1467 9r149 4c3467 6c3467 7c3467 9c3467 46n5 6n7 467b5} 0 Links = {} -->

Image

Suggestion, if you put a small gap between layers it might make the data easier to see. Or some other character?

Code: Select all: N:......... ......... ......... ....X.... ......... ....X.X.. ......... ......... ......... R:......... ......... ......... X.XX..X.. ......... ..XX.X..X X..X.XX.. ......... X .X....X C:......... ......... ......... ..XX.XX.. ......... ..XX.XX.. ..XX.XX.. ......... ..XX.XX.. B:......... ......... ......... ....X.... ......... ....X.... ....X.... ......... ......... 1 2 3 4 5 6 7 8 9

PS. Did you see the second example that I placed in the Great Monster Loops thread? That one has no box sets.
.

by **champagne** » Thu Nov 20, 2008 4:16 am

Hi Allan,

1)Maybe you need to re-check this set group.
It's ok for me if you add the two cells/nodes of the target N24 and N68

2)In the grid image, all (red) rows and many (green) columns have some candidates only covered by one set. These must become linksets.

As you can see in my diagram, all candidates in the columns have at least one row or one cell/node attached.
All are eligibles as sets.
Cells/Nodes 46N5 are also eligible as sets.

3) However, they are arranged in a way that much of the pattern cannot not be covered by strong sets.

See my diagram. It's not exactly the same list of sets as I indicated (9B5 and 9r6 added, 6N7 erased, but I hope this does not change the scope;

4)Also, the number of permutations is over 8000000 but should be about 2000.

Here I have to be cautious. My solver counts 1033 permutations, but may be this is thru the use of some cells/nodes in the line NV.
Anyway, it is a "relatively" small number. This is something you feel when you try to explore manually the solution.

5)Suggestion, if you put a small gap between layers it might make the data easier to see. Or some other character?
Blank seems to be good. Immediate effect.

6) PS. Did you see the second example that I placed in the Great Monster Loops thread? That one has no box sets.

Yes, I have seen it.

. still very different from that one,
. I was not sure about the cleanings done out of it??
. is it an alternative to the first loop
. did it come after with other eliminations??

I did not try to answer the question.
In place, I looked at it to try to find an example illustrating a new idea I had after having analyzed your example crossing ALS/ACs, but it did not materialize. (I'll talk of it if and when I have an example)

It seems that despite our clues, our expert "ttt" is still suffering to find out something simple.

champagne

by **champagne** » Thu Nov 20, 2008 4:36 am

Hi ttt

ttt wrote:From above we can eliminate at least two candidates: r46c3<>1,
ttt

Again, your findings are out of the field suggested by the solver.
Easiest target after 2r2c4 and 5r6c8 are supposed to be

4: r1c28 r3c4
6: r6c8
7: r1c25 r6c2 r7c9
9: r6c9

If you get something we can digest, don't hesitate to communicate on it.

I have a question. Did you ever use in your solutions some patterns as

Code: Select all: y x x x x x x x x x x x x z

where
. all xyz are candidates of the same digit
. no other candidate in columns.

in that picture y = z is a strong link.

In a similar way, in that pattern

Code: Select all: y x x x x x x x x x z

y and z are normally both in or both out
(precise conditions should be written.)

It seems to me that such patterns could be used in connection with Allan SLGs;

champagne

by **Allan Barker** » Thu Nov 20, 2008 5:57 am

ttt wrote:Hi Allan & champagne,
I consider this:
1- Look r2c45 with candidates 4,6,7,9 => at least TWO of [(6)r1c2, (4)r2c2, (7)r2c2, (4)r2c8, (9)r2c9] must be true – Group 1.
2- Look r8c56 with candidates 4,6,7,9 => at least TWO of [(9)r8c1, (4)r8c2, (6)r8c8, (7)r8c9] must be true – Group 2.

From above we can eliminate at least two candidates: r46c3<>1, presenting as diagram for this is not too complex but not nice then I’m still thinking more…

Hi ttt,

I agree, in rows 2 and 8, both groups must have TWO of the candidates = true. The FM initial-loops had the same kind of logic. Nice work. I call these double inference sets.

Champagne wrote:Again, your findings are out of the field suggested by the solver.
Easiest target after 2r2c4 and 5r6c8 are supposed to be

4: r1c28 r3c4
6: r6c8
7: r1c25 r6c2 r7c9
9: r6c9

When I use floors 4679 like Champagne then I get these same 11 eliminations. But I have to do it all manually. So I don't think r46c3<>1 is in these floors.

However, the row 2 and 8 double inference sets are powerful logic. I think it's possible to eliminate r46c3<>1 with logic that is outside the 4679 floors.

Champagne,

Champagne wrote:
Code: Select all
N:...............................X.................X.X............................. R:...........................X.XX..X.............XX.X..XX..X.XX...........X..X....X C:.............................XX.XX.............XX.XX....XX.XX.............XX.XX.. B:...............................X.................X........X...................... 1 2 3 4 5 6 7 8 9 =37 sets and likely some of theese used as well NV.xxxxxx...x.xx......xxx....x.x.x.xxxx..x.x.xx..x.x.x.x...xxx.......xx......xxx... 1 2 3 4 5 6 7 8 9

Ah, what does NV mean? Should I be using some of these sets as well? Could this be the difference?

by **ttt** » Thu Nov 20, 2008 6:39 am

champagne wrote:If you get something we can digest, don't hesitate to communicate on it.

Yes, I’m still thinking…
For patterns you suggested, I don’t know. I thought simple that if we have two strong sets A=B & C=D => at least one of [(A&C), (A&D), (B&C), (B&D)] must be true then the effect is difference with we use A=B, C=D separate. Back to the puzzle with my last post then we have 4 “true” in the same time, based on that I found r46c3<>1, presenting it is not nice and I’m still thinking more, hope find something…

ttt

by **champagne** » Thu Nov 20, 2008 6:54 am

Hi Allan,

Allan Barker wrote:
Champagne wrote:Again, your findings are out of the field suggested by the solver.
Easiest target after 2r2c4 and 5r6c8 are supposed to be

4: r1c28 r3c4
6: r6c8
7: r1c25 r6c2 r7c9
9: r6c9

When I use floors 4679 like Champagne then I get these same 11 eliminations. But I have to do it all manually.

I'll try. I have not yet launched that search in the program.

So I don't think r46c3<>1 is in these floors.

However, the row 2 and 8 double inference sets are powerful logic. I think it's possible to eliminate r46c3<>1 with logic that is outside the 4679 floors.

may-be, maybe not. ttt has a bad habit, he is using intensively Unicity

BTW, the program checked all possibiities combining up to 4 floors. it found nothing else. Unless ttt used the fact that 2 candidates were already cleared, he should use a minimum of five floors or something as unicity to achieve that elimination

Champagne,

Champagne wrote:
Code: Select all
N:...............................X.................X.X............................. R:...........................X.XX..X.............XX.X..XX..X.XX...........X..X....X C:.............................XX.XX.............XX.XX....XX.XX.............XX.XX.. B:...............................X.................X........X...................... 1 2 3 4 5 6 7 8 9 =37 sets and likely some of theese used as well NV.xxxxxx...x.xx......xxx....x.x.x.xxxx..x.x.xx..x.x.x.x...xxx.......xx......xxx... 1 2 3 4 5 6 7 8 9

Ah, what does NV mean? Should I be using some of these sets as well? Could this be the difference?

Sorry for the vocabulary. I guess it is "Node Vector". In other places I used "OF" for Nodes having candidates out of the floors.

This bit field points on all cell/nodes having at least 2 candidates in the floors and candidates out of the floors. They have to be checked for "always assigned" in the permutations. What I have to see is whether in the slimming process they have been used as sets. (or whether use of them changes the resuts) That's a reason why I stay very cautious

I doubt they have to be used, but it could be.

champagne

by **ttt** » Sat Nov 22, 2008 5:18 am

Hi All,

Code: Select all: *-----------------------------------------------------------------------------* | 1238 123478 12(47) | 2479 234579 4579 | 35(49) 12345 6 | | 23(6) 23(47) 5 | 2(4679) 23(4679)1 | 8 23(4) 23(9) | | 1236 9 12(46) | 246 23456 8 | 3(4)5 7 1235 | |-------------------------+-------------------------+-------------------------| | 1569 157 1(679) | 8 4679 2 | 35(4679)13456 13579 | | 5689 578 3 | 4679 1 4679 | 2 4568 5789 | | 4 1278 12(679) | 5 679 3 | (679) 168 1789 | |-------------------------+-------------------------+-------------------------| | 1235 6 12(4) | 1247 24578 457 | 35(7) 9 23578 | | 25(9) 2(4)5 8 | 3 25(4679)5(4679) | 1 25(6) 25(7) | | 7 1235 12(9) | 1269 25689 569 | 35(6) 23568 4 | *-----------------------------------------------------------------------------*

On finding how to present deductions, I found this but not sure…
Based on Steve’s concept for SK loop, look 4’s, 6’s, 7’s, 9’s on row 2&8 and col. 3&7 with 16 “true” and boxes 2,3,4.6.7.8.9 each box contain max. two “true” for 4,6,7,9 then:
1- If box 1 contains two “true” => SK loop and deduct some…
2- If box 1 contain three “true” => some cases with 4’s, 6’s ,7’s at r2c1, r2c2, r1c3, r3c3 and one of boxes 2,3,4,6,7,8,9 contain only one of 4’s, 6’s, 7’s, 9’s
Then I found something quite interesting but not sure and need your help, I’m too headache…

ttt

by **Allan Barker** » Sat Nov 22, 2008 7:17 am

ttt,

So close! However, I don't think this works because it has 9 boxes not 8 boxes, thus it has 14 true sets and 15 weak linking sets. As you say, the real SK loop has 14 true and 14 box/cell. The extra box here makes the logic rank 1 and it does not eliminate candidates. My software will show if it does.

The problem is layer 4 is not symmetrical like layers 679.

Layers 679 true( 2 rows + 2 columns) weak (2 box)
Layers 4 true( 2 rows + 2 columns) weak (3 box)

See the picture below, check to see I connected it correctly. Maybe you can see something else that I can't see.

Thumbs (click below)

by **champagne** » Sat Nov 22, 2008 7:57 am

ttt wrote:Hi All,
On finding how to present deductions, I found this but not sure…
Based on Steve’s concept for SK loop, look 4’s, 6’s, 7’s, 9’s on row 2&8 and col. 3&7 with 16 “true” and boxes 2,3,4.6.7.8.9 each box contain max. two “true” for 4,6,7,9 then:
1- If box 1 contains two “true” => SK loop and deduct some…
2- If box 1 contain three “true” => some cases with 4’s, 6’s ,7’s at r2c1, r2c2, r1c3, r3c3 and one of boxes 2,3,4,6,7,8,9 contain only one of 4’s, 6’s, 7’s, 9’s
Then I found something quite interesting but not sure and need your help, I’m too headache…

ttt

Too late for me, I have to get out this evening, but you have stressed on a very interesting point with that "nearly complete SK loop";

I can bring in elements that can help you.

to come to morrow.

champagne

by **Allan Barker** » Sat Nov 22, 2008 8:08 am

Champagne wrote:I am very surprised than you can't do anything out of my group of sets.

I am not so suprised, I think it means that your box theory works very well. If I remember right, even Golden Nugget had several eliminations that were similar.

Champagne wrote:I revised the design to be closer to yours, and herebelow is the final status.
I'll add this one to the Monster Loop thread, it is the all-column variety, my last post was the all-row variety. It is very similar to FM first loop, so I thought you would have no problem to establish the left part of the diagram is rank 0.

Yes, the left side is rank 0, but only two linksets, N24 and N86. Same was true of FM. The image in the FM thread showed the rank 0 linksets in black.

Champagne wrote:If not, could you explain why and how you account rank in such a diagram.

The full explanation is not very simple. In brief, every candidate in cell sets N45 and N65 is a triplet. Therefore, two triplets are always occupied lowering the overall rank by 2. The un-occupied triplets also lower the rank in some regions that includes N45 and N65. In the end, only N45 and N65 are rank 0 for all possible triplet configurations. Thus, they are the ones that are really rank 0.

by **champagne** » Sat Nov 22, 2008 11:32 pm

Hi ttt,

On finding how to present deductions, I found this but not sure…
Based on Steve’s concept for SK loop, look 4’s, 6’s, 7’s, 9’s on row 2&8 and col. 3&7 with 16 “true” and boxes 2,3,4.6.7.8.9 each box contain max. two “true” for 4,6,7,9 then:
1- If box 1 contains two “true” => SK loop and deduct some…
2- If box 1 contain three “true” => some cases with 4’s, 6’s ,7’s at r2c1, r2c2, r1c3, r3c3 and one of boxes 2,3,4,6,7,8,9 contain only one of 4’s, 6’s, 7’s, 9’s
Then I found something quite interesting but not sure and need your help, I’m too headache…

I promised somethinn. I don't know if it will help, but this is one step in your direction.
This is based partly on "virus patterns", AC2 with specific properties I ahve described one year ago in my main post "full tagging".

http://forum.enjoysudoku.com/viewtopic.php?t=5624&postdays=0&postorder=asc&start=0

These virus patterns are one way to describe SK loop. As we have here a "Nearly complete SK loop", your can work with them.

Code: Select all: 1238 123478 1247 |2479 234579 4579 |3459 12345 6 236 2347 5 |24679 234679 1 |8 234 239 1236 9 1246 |246 23456 8 |345 7 1235 --------------------------------------------------------- 1569 157 1679 |8 4679 2 |345679 13456 13579 5689 578 3 |4679 1 4679 |2 4568 5789 4 1278 12679 |5 679 3 |679 168 1789 --------------------------------------------------------- 1235 6 124 |1247 24578 457 |357 9 23578 259 245 8 |3 245679 45679 |1 256 257 7 1235 129 |1269 25689 569 |356 23568 4

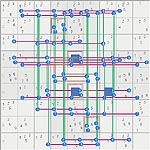
Here after the "Nearly SK loop" with non conform patterns at both ends;

Code: Select all: r2c12 r2c89 r13c7 r79c7 r8c89 r8c12 r79c3 r23c1 467 23 23 49 49 35 35 67 67 25 25 49 49 12 12 467 X Y X Y X Y X Y X Y X Y X Y

The main properties of "virus patterns" are summarized here below

from left to right #Y => #Y and X => X
#(2&3)r2c89 => #(4&9)r3c17 . . . => #(4&9)r79c3 => #(2&3)r23c1
(2&3)r2c12 => (4&9)r2c89 . . . => (1&2)r79c3 => 2 fo (467) r23c1
from right to left #X => #X and Y => Y
#(1&2)r79c3 => #(4&9)r8c12 . . . => #(4&9)r2c89 => #(2&3)r2c12
(1&2)r23c1=>(4&9)r79c3 . . . =>(4&9)r13c7 => 2 of(467) r2c12

if #Y and #X we have at least one valid on each end giving on general property of virus pattern chains:

In a virus pattern chain, at minimum, 2 out of the four digits in the ends are true.

This is extended here to "2 of the six digits", so a minimum of 2 out of
4r2c2;6r2c1;7r2c3 4r13c3;6r3c3;7r3c3
are true.

Now one finding of the solver : (4&9)r2c89 is not validHe did it thru complex AICs nets, but you can show it in a very simple equivalent way along the "virus patten chain"

(4&9)r2c89 =>(3&5)r13c7 => (6&7)r79c7 => (2&5) r8c89 => (4&9) r8c13 => (1&2)r79c3

After partial cleaning we see that r5c46 must be 49, but then we have a deadly pattern for 67 in column 5.

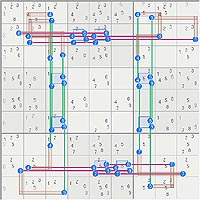
Code: Select all: 1238a 123478A 47â |2479 234579 45S79 |35 1e2 6 236t 237à 5 |267 2367 1 |8 4 9 1236 9 46V |246 2345P6 8 |35 7 1E2 ----------------------------------------------------------------------- 156 157 679 |8 4n679 2 |4o79 1356 1357 568A 578 3 |4679 1 46w79 |2 568 578 4 12b78å 679 |5 679 3 |79 168 178 ----------------------------------------------------------------------- 3g5 6 12 |1d24 2458c 45 |7 9 38C 9i 4H 8 |3 67 67 |1 25 25 7 3G5 12 |1D269 2568C9 569 |6x 38c 4

This gives a second clue: we can not have (1&2) r13c3.
One at least out of 4r13c3;6r3c3;7r3c3 must be true.

That's all for the time being. I hope it can help you.

BTW, it shows as well that some of my solver findings can be improved in a "very simple way".

champagne

by **ttt** » Sun Nov 23, 2008 2:15 am

Hi Allan & champagne,
Thanks for your help! I'm studying your posts and hope something useful.

ttt

by **ronk** » Sun Nov 23, 2008 3:17 am

Allan, champagne, ttt, one has to backtrack through the thread to here to figure out you're talking about tarx0075. :idea:

by **champagne** » Sun Nov 23, 2008 4:23 am

ronk wrote:Allan, champagne, ttt, one has to backtrack through the thread to here to figure out you're talking about tarx0075.

That's OK, but if the solution for tarx075 was the topic, should not it be in the "general puzzle" group.

On the other side, we have switched on that puzzle pushed by our friend "ttt" and we are all three deeply involved in our "discussions", "thinkings", "researchs" about how to start on hardest puzzles.

I just hope something good will come out of it

BTW I have a complete solution for that puzzle, just what you don't like: computer made, long, boring.

I agree with you, we have enough of such solutions and we have to look for something lighter

champagne

by **coloin** » Sun Nov 23, 2008 5:18 am

ive been following your commendable efforts

heres something lighter, hopefully useful.

w.r.t. the tarx0075 puzzle

here are the pms

Code: Select all: +----------------------+----------------------+----------------------+ | 1238 123478 1247 | 2479 234579 4579 | 3459 12345 6 | | 236 2347 5 | 24679 234679 1 | 8 234 239 | | 1236 9 1246 | 246 23456 8 | 345 7 1235 | +----------------------+----------------------+----------------------+ | 1569 157 1679 | 8 4679 2 | 345679 13456 13579 | | 5689 578 3 | 4679 1 4679 | 2 4568 5789 | | 4 1278 12679 | 5 679 3 | 679 168 1789 | +----------------------+----------------------+----------------------+ | 1235 6 124 | 1247 24578 457 | 357 9 23578 | | 259 245 8 | 3 245679 45679 | 1 256 257 | | 7 1235 129 | 1269 25689 569 | 356 23568 4 | +----------------------+----------------------+----------------------+

If we remove a given clue from this puzzle say the 8 @ r3c6, we get a subpuzzle with more than 1 solution.

The "real" pm board of this subpuzzle [as opposed to the above "virtual" board] reveals many elimiinations. Particularly the 2 @ r6c2 can be inserted !.

Does this indicate the weak spot in this puzzle ?

Edit.....ignoring the complexity of the loops...analysis of "floors" 178/1278 gives this insertion perhaps.

C

The New Sudoku Players' Forum

AIC's net equivalent to forcing net