StrmCkr wrote:
- Code: Select all
-------------------------
| X X X | . . . | .-x . |
| / X / | . . . | . . . |
| / X / | . . . | . . . |
-------------------------
| . . . | . . . | . . . |
| . . . | . . . | . . . |
| . . . | . . . | . . . |
-------------------------
| / x / | . . . | / x / |
| X X X | . . . | x x x |
| / x / | . . . | / x / |
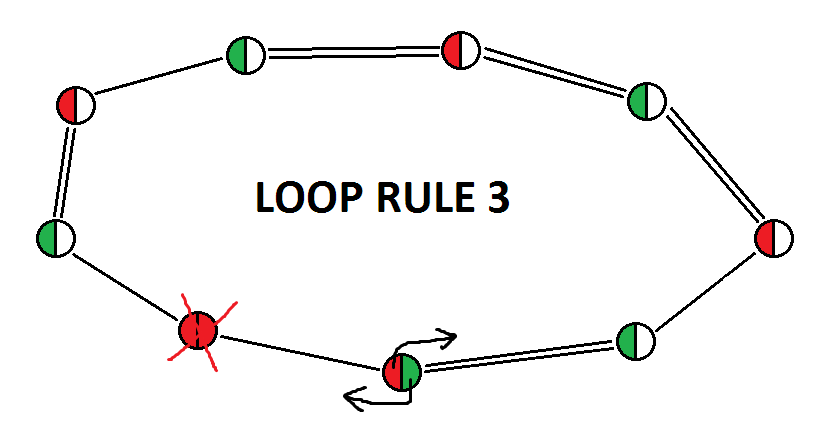
-------------------------r8c123-r8c789=r79c8-r1c8-r1c123=r23c2-r79c2=r8c123
L.R.3: r1c8
the way i would read this is
R8C123(on) => r8c789{off} => r79c8 (on) => r1c8 (off). {stalls on the weak link here}
[...]
id read that you started on a weak link and not a strong link
[...]
As already said, my algorithm always starts from a strong link, in this case r79c2=r8c123 (but it could also have been r8c789=r79c8 or r1c123=r23c2), where r8c123 is the starting node and r79c2 the arrival node.
Proof that it is a loop rule 3 is specified here:
Mino21 wrote:loop rule 3 is characterized by:
1) at least one weak link;
2) one subsequence of two consecutive weak links;
3) no even subsequence of consecutive strong links;
4) any number of odd subsequences of consecutive strong links;
5) odd number of nodes (but this is a consequence of the previous points)
Proof: starting from the node that starts the subsequence of two consecutive weak links, and assuming once it is true and once it is false, we will obtain that the node that sees two weak links is false in both cases, which will allow us to eliminate the candidate in it;
But actually, now that I think about it, it can be proved even more simply: starting from the node that sees two weak links, and assuming is true, we will obtain a contradiction, which will allow us to eliminate the candidates in it.
That said, I don't really understand why you give so much importance to the order in which I write the cycle ... it's a cycle!
My search algorithm does not go on in terms of ON and OFF, but is simply based on the characteristics of the part of the cycle constructed so far, taking into account the following positions:
Mino21 wrote:b) a valid loop must have the following characteristics:
- at least 4 nodes;
- at least a weak link;
- at most an even subsequence of consecutive strong links or a subsequence of two consecutive weak links;
- (any number of odd subsequences of consecutive strong links).
So is my approach equivalent to the "official" one? Or not? I still haven't figured it out!
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
@P.O. and @Pat
The basic problem is that you try to understand what I write through the filter constituted by the "official" conventions on x-cycles, ignoring my point of view on the problem reported in full in this post.
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
eleven wrote:Mino21 wrote:It may seem strange to you, but I used the SudokuWiki site only to understand the basic idea of the various solving techniques, but then, both for x-cycles and some other techniques, I built my own logic settings and algorithms.
lol, you didn't even understand the most basic logic definition of a strong link, ignored all the posts addressing it and insisted on your own weird one. This is the cause of all your troubles.
You are not saying anything new, I myself have repeated several times that:
Mino21 wrote:the concepts of "alternating strong_link-weak_link", "discontinuity" and "strong links acting as weak links" are completely absent in my approach and were not necessary for my problem modeling
If those who did not want to deepen my point of view on the problem has avoided repeating the same things over and over, by answering questions never asked and forcing me to reiterate it, this topic would have 3-4 pages less!
I honestly think that a problem can also be interpreted with different models that still provide equivalent results ... I don't want to force anyone to answer me, but I was simply asking if my approach was correct from a logical point of view, and it makes no sense to answer this request by bringing up a different approach.
I hope I was clear this time...