So can all these 3 cases
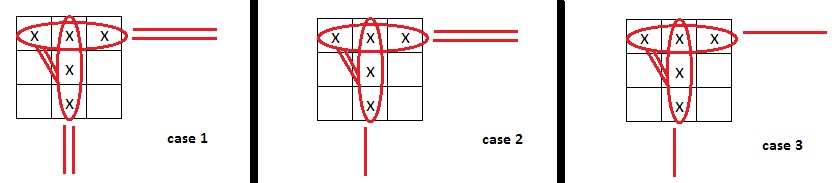
be part of a valid cycle?

yzfwsf wrote:Strong and weak must alternate in the AIC or Cycle.
Mino21 wrote:in practice two consecutive group-nodes can have a cell in common only if connected by a strong link, right?
yzfwsf wrote:In a word, the state of overlapping cells is indeterminate, and this uncertainty cannot affect subsequent logical reasoning.
Mino21 wrote:two consecutive group-nodes cannot under any circumstances have a cell in common
eleven wrote:"(r8c8 r9c8)--(r8c8 r8c9)"
This is not a weak link, which would mean, that if a digit is on one side, it cannot be on the other side. But r8c8 is on both sides.
Pat wrote:does this help?
Mino21 wrote:Isn't this:Mino21 wrote:two consecutive group-nodes cannot under any circumstances have a cell in common
a consequence of this:eleven wrote:"(r8c8 r9c8)--(r8c8 r8c9)"
This is not a weak link, which would mean, that if a digit is on one side, it cannot be on the other side. But r8c8 is on both sides.
?
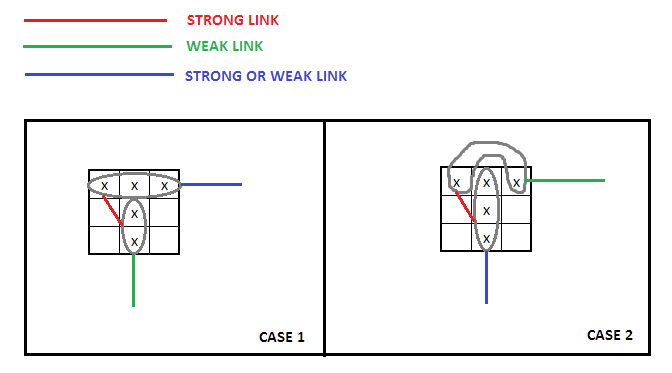
Alternatively, could you give me an example of a cycle with two consecutive group-nodes sharing a cell?
c1 c2 c3
+---+---+---+
r1 | x | x | x |
r2 | | x | |
r3 | | x | |
+---+---+---+two consecutive group-nodes cannot under any circumstances have a cell in common
Cenoman wrote:A strong link is equivalent to the logical equation A OR B = TRUE
A weak link is equivalent to the logical equation A NAND B = TRUE