Fata Morgana
It was recently pointed out that the puzzle Fata Morgana, FM, stumps logic solvers that can solve Golden Nugget, and that FM is much harder to solve using grid solvers based on backtracking and even Algorithm X. Contrary to this, FM is easily solved with a freeform set logic solver, which rates the puzzle as only a medium monster. It initially seems that this difficulty is more illusionary than real, like a mirage or a fata morgana (cool name). Like a mirage however, the illusion can only be seen from certain perspectives. Obviously something is different about this puzzle, but what?
It is of course interesting to understand anything that can cause such trouble for different solving methods. The anomaly also asks the question what does it mean to say a puzzle is difficult?
Fata Morgana compared to Golden Nugget and Easter Monster
Although not necessary, it's helpful to include Easter Monster in the comparisons. The 3 puzzles, GN, EM, and FM are first compared using two different kinds of grid solvers, one of which uses backtracking with simple Sudoku moves, and the other uses a cover process similar to Algorithm X. Not only is FM very difficult, but GN is left as the easiest of the three.
- Code: Select all
Backtrack Algorithm X'
Fata Morgana 191 129 arbitrary operations
Easter Monster 72 47 arbitrary operations
Golden Nugget 49 46 arbitrary operations
Set Logic solutions to these puzzles show exactly the opposite trend. The charts below show the relative difficulty of each move for solutions of GN and FM. Difficulty is based on both the number of strong sets required (blue) and the total number of nodes (red). Fata Morgana is obviously much easier and this is true of the entire solution path, not just some moves. (Easter Monster, not shown, is in between the two as far as difficulty)
Golden Nugget
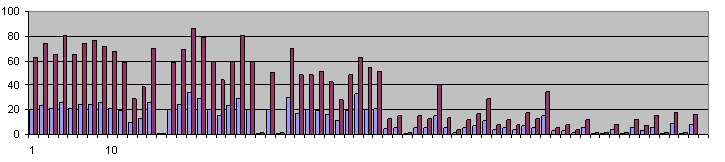
Fata Morgana
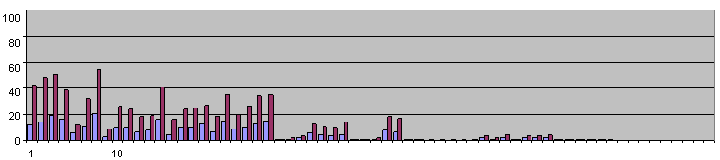
Step by step rating of different methods
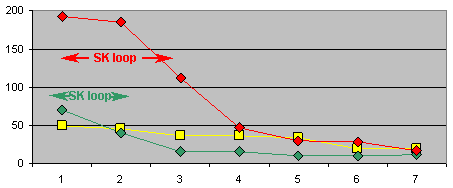
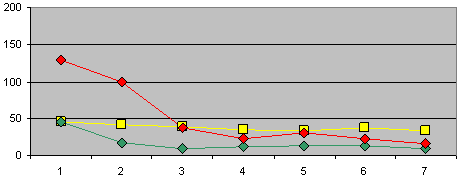
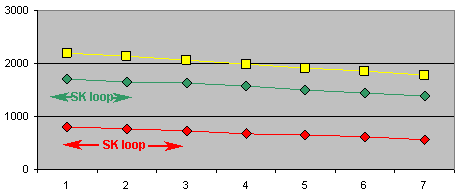
Grid solvers only show the work required to solve a puzzle. However, one way to see what's happenging is use the grid solvers after each elimination and then compare the work each solver does to solve each grid. The graphs below compare each method for all three puzzles. Comparing the first seven grids is enough to find part of the answer, which is that the anomoly is present only for the first 3 moves of FM. EM shows a slight anomaly for the first 2 moves and GN has none. Therefore, the first moves are casuing the problems but not for the set solver. As indicated in the graphs both EM and FM have initial SK loops but these loops are not the real problem. The numbers from each solver are arbitrary units, which are not related between solvers.
KEY: red = FM, green = EM, yellow = GN.
Backtracking
Algorithm X'
Set Solver
The anomaly and SK loops
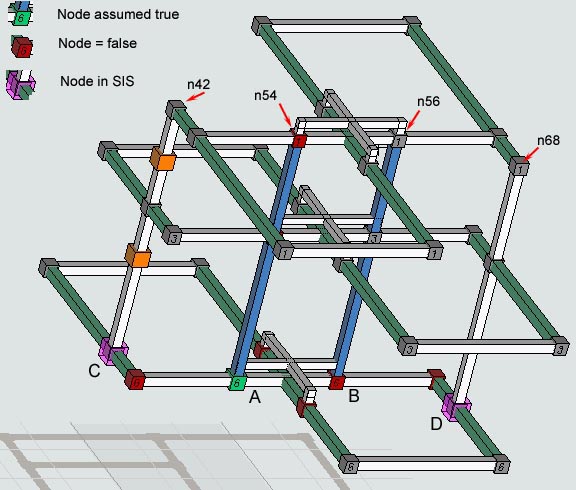
A look at FM and EM logic reveals that the true anomaly in not becasue SK loops are present but becasue the loops in FM have no bivalue sets (see logic below). In fact, the FM loops are somewhat smaller that the EM loops yet cause the puzzle to be several times more difficult. Most likely, some solvers could have difficulty solving a large structure made entirely of sets with 3 or more candidates. The role of the SK loop may be only to prevent the solver from finding other solution paths. Node designations are not included below, the path structure that a solver must follow is more important.
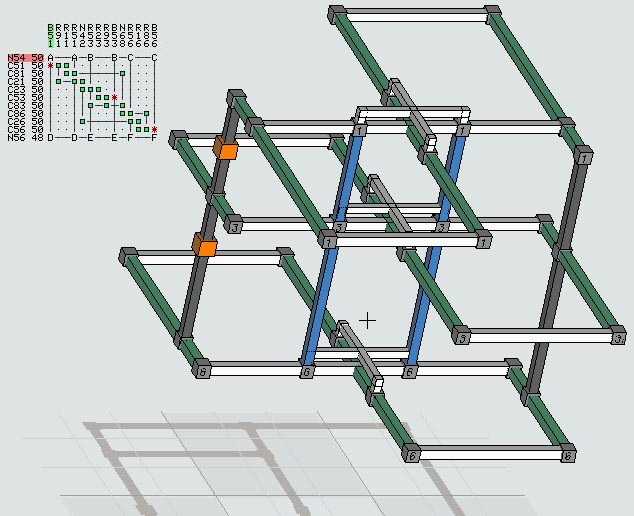
Fata Morgana, first SK loop A symbolic set logic diagram for the first of 3 SK loop eliminations. The logic has 11 strong sets all of which have 3 candidates. The second SK loop (not shown) has 14 strong sets, all of which have 3 candidates. ( = strong set, | weak set, * node, A, B, etc. triplet node)
- Code: Select all
A===============B================C
/ \ / \ / \
/ \ ____/ \_____ / \
| | | | | |
*==*==|==* | | | |
* | | | | | | |
| | *==*==|==* | | |
| | | | | | | |
| *==*=====|==|==* | | |
| | | | | | | |
| | *==*==|==* | | |
| | | | | | | | |
| | *==|==*==|==* | | |
| | | | | | | | | |
| | | | | *==*==* | |
| | | | | * | |
| | | | *========|=====*==* |
| | | | | | | |
| | | *===========|==*==* | |
| | | | | | | *
| | | | *==|==*==*
| | |____ _____| | |
\ / \ / \ /
\ / \ / \ /
D===============E================F
Easter Monster, first SK loop: A symbolic set logic diagram for the first of 2 SK loops eliminations. The logic has 16 strong sets of which 4 are bi-value. The second EM SK loop is much smaller. ( = strong set, | weak set, * node)
- Code: Select all
*==*
| |
| *==*==============*
| | | |
| *==*===========* |
| | | | |
| *==*==* | |
| | | *========*==*
| | | | |
| | *===========*==*
| *==*==* | |
| | | | |
| *==*===========* | |
| | | | | |
| *==*========* | | |
| | | | | *===========*
*==============* | | | | |
| | *==*==* |
| | | |
| | *==*==* |
| | | | |
| *===========*==* |
| | | |
*==============*==* |
| |
*==*
Intrinsic difficulty (complexity), thoughts
Unlike a mirage, it's hard to explain away FM's difficulty as completely artificial. It is also hard to maintain that it is all real. Surely, some solvers look for initial bi-value sets or maybe even require them. However, Algorithm X is not restricted in such a way. Perhaps the only safe thing to claim is that each puzzle must have an intrinsic difficulty.
Rating puzzles by a set of rules like SE seems (to me) to work surprisingly well, and a precisely defined set of resolution rules may work even better. However, here lies the real illusion as FM demonstrates, any (reasonable) set of rules will work well when referenced only to itself. Two sets of rules can have significant differences yet each set is internally consistent. The only point I make is that intrinsic difficulty has intrinsic value (hah, can't argue with that!). Ultimately, human experience comes into play, which can be different from either rule based or intrinsic scales.
Edit: 1)put labels on diagrams. 2) Key to graphs
Allan
Without your help, I think all of us will have strong diffiulties to understand it and the kind of clearings that can be done out of it.
