The New Sudoku Players' Forum

[Allan Barker]

Believe me ....

I believe you, it has taught me the real meaning of NP complete, no shortcuts.

If the matrix refers to “sets” r12 and r42, they should always be occupied.
If the matrix is a “digit 2” map, p142 and p612 are defined in the first line and will be “0” in any other place. Then can be cleared.
If this second point is the right answer, it makes sense.

I think your second point is closest. Just to make sure, I extended your example with a swordfish and I labeled the nodes. Each permutation is one possible assignment of true/false values for all nodes in the logic, according to the Sudoku rule.

Code: Select all

2 digit plane with node labels - X-Wing

c      c
0      4

A - -  B - -    row 0
- - -  - - -
- - -  - - -

C - -  D - -    row 4
- - -  F - -
E - -  - - -

               ABCD EF
             +--------------
Permutations | 0110 00
             | 1001 00
               ^^--------- row 0
                 ^^------- row 4
               ^-^--^----- col 0
                ^-^--^---- col 4

2 digit plane with node labels - Swordfish

- - -  - - -  - - -
- - -  - - -  - - -
- - A  - B -  C - -

- - -  - - -  - - -
K - D  - E -  F - -
- - -  - - -  - - -

- - G  - H -  I - J
- - -  - - -  - - -
- - -  - - -  - - -

               ABC DEF GHI JK
             +----------
Permutations | 001 100 010 00
             | 001 010 100 00
             | 010 001 100 00
             | 010 100 001 00
             | 100 010 001 00
             | 100 001 010 00
                           ^^-- elimination


[champagne]

I think your second point is closest. Just to make sure, I extended your example with a swordfish and I labeled the nodes.

I came to the conclusion that what is above was the right understanding. I will discard my post in the other thread and I'll work on that one to be sure I got it now. Thanks for your effort.

Hope others will find also some reasons to be confident in that general process.

[StrmCkr]

thanks allan for the detail on the baby sk loop.

heres a big hint...

you can also tie that layer backing ito the standard sk loop.
producing larger amount of eliminations. i don't have detail on it.
i was tryign to show champane it but its lost in translation...

champane: further or discussion on "in rod we trust"
allans detail on the loop is the one i was tryign to show you

but
i extended it back into the standard skloop and found more eliminations. that is what i sent you.

[champagne]

champane: further or discussion on "in rod we trust"
allans detail on the loop is the one i was tryign to show you

I did not work on that loop. I wanted first to understand loop2 of Allan in say "common logic".

Something you should like I believe I got it using a "pair extending technic", what you like that much. I need a last check before publishing, but you can find it as well with the following guidelines.

1) try the three pairs solving r5c46 1&3 1&6 3&6.

2) In the development, concentrates on candidates Allan so kindly told us they should disappear.

3) Don't forget a very important point to do it quickly: with the findings of the first loop, You have in each scenario a double exclusive or in cels r4c2 r6c8.


4) last clue, in column 5, you can show that in nodes having two of the scenario digits, they can be discarded. If you have none, you'll find a nice loop.


- I have to confess that wthout Allan indications I would never had found that,
- I see a performing way to include this in my solver in general terms, but this does not change my view on willingness to develop Allan Logic as an alternative (and may be still complementary) path in my solver.

[champagne]

Hi,

As promised, a way to establish FL loop2 using classical logic.

At the time where degenerated patterns for UR are discussed in a wide way, it gave me an idea to include the active pattern found here in my solver.

I am normally working, at level 4, on AC2 (say to be simple two cells, four digits). If I process the 136 136 pattern as a degenerated AC2, I am not sure I'll find loop1, but for sure, loop2 would come after loop1.


champagne

[Allan Barker]

you can also tie that layer backing ito the standard sk loop. producing larger amount of eliminations. i don't have detail on it.
i was tryign to show champane it but its lost in translation..

Yes, I did see similar things. There are multiple loops and sometimes one loop is a subset of a larger loop with more eliminations. I also noted layers are important units and saw your comment about multiple fish layers in the other thread.

I did not work on that loop. I wanted first to understand loop2 of Allan in say "common logic".

Along the same lines. FM loop 2 will eliminate the same two candidates as FM loop1, 2r4c2, 4r4c2, meaning FM loop 1 is not needed, if you have FM loop2.

It is also very interesing that you can so easily update your layer 4 algorithm given data from such a different source. But, I guess all methods should have some common ground.

"In rod we trust"??

Oh my rod!
.

[StrmCkr]

champ
great to hear you found a way to incorperate my take on solvig with
the aid of allan for helping explain it where i fail yes that is how it would resolve Fm. as you have shown


are you finding the same thigns allan? with layered fish?

"re quote" its a simpson quote.
a inanimate carbon rod gets employee of the month over homer simpson. the quote at the end of the show is.
"in rod we trust"

allan further to my comment of layered fish.

cloud bay.
has the 4 layered fish.

in testing for a
5 layer fish
i havent found one that exsits. but it could
but i have doubts ive tryed building puzzled as well..

[champagne]

Along the same lines. FM loop 2 will eliminate the same two candidates as FM loop1, 2r4c2, 4r4c2, meaning FM loop 1 is not needed, if you have FM loop2.

I'll comment on that in your main thread

It is also very interesing that you can so easily update your layer 4 algorithm given data from such a different source. But, I guess all methods should have some common ground.

Don't be so optimistic. I see exactly what is the proper way to handle it and I do'nt foresee any difficulty. It has still to be done. May be one week full time to do it in a clean way.

In a similar way, I have a good idea now about "a performing analyser of permutations". It's not done. Comment on "the collection of sets"will come in the main thread.

Last but not least, I am not really surprised that quite different ways to fight against a puzzle can merge somewhere. This is somethng we see every day and the more I understand your method, the less I see reasons why it could different here.

[Allan Barker]

FM, GN, and EM, Golden Nugget Morphed

I have found one last piece of evidence in the comparison between the puzzles, GN, EM, and FM, and TR. Although both EM and FM have large, symmetric initial loops, FM's unusually difficult eliminations were probably due to the lack of bi-value sets in its initial loops, not because of the loop itself.

The final piece of evidence is the discovery of symmetrical loops in Golden Nugget. Although this Golden Nugget Solution shows multi-layered structures, it had no symmetry. However, morphing the puzzle reveals initial loops that are very similar to FM. The structure below has 4 single-digit layers plus a very small layer 6 made of a single bi-value set, similar to Tungsten Rod. GN is very difficult but shows no abnormal initial difficulty like FM. In other words, all 4 puzzles have similar looped structures but FM is the only one without a bi-value set.

Code: Select all

Golden Nugget Morph - Set Logic

E0[  54 Nodes, Rank 1:
     17 Sets = {1247r1 1247r5 1r6 1247r9 6c4 247b5}
     18 Links = {27c1 14c2 1247c5 47c8 12c9 145n4 59n6 1b4}
     --> (9n6) => r9c6<>3

Golden Nugget Morph - Pencil Grid

  +-----------------------------------------------------------------------------+
  | 35(2)   35(4)   8       | (1247)  35(1247 6       | 9       35(7)   35(1)   |
  | 3569    7       456     | 1489    13459   1348    | 136     2       13568   |
  | 1       3569    256     | 2789    23579   2378    | 367     35678   4       |
  +-----------------------------------------------------------------------------+
  | 26789   4689    2467    | (2467)  (247)   5       | 23467   1       23689   |
  | 69(27)  69(14)  3       | (12467) 8       (1247)  | 5       69(47)  69(2)   |
  | 25678   4568(1) 24567(1 | 3       (1247)  9       | 2467    4678    268     |
  +-----------------------------------------------------------------------------+
  | 4       13568   156     | 1289    1239    1238    | 1236    3569    7       |
  | 3578    2       157     | 14789   6       13478   | 134     3459    1359    |
  | 36(7)   36(1)   9       | 5       3(1247) 3(1247) | 8       36(4)   36(12)  |
  +-----------------------------------------------------------------------------+

Golden Nugget Morph - Logic Diagram

            p452==================================================p562E=p542B=p442
            p652                                                   |     |     |      Digit 2 Layer
             |                                                     |     |     |
             |                p592==p512==========================p562E=p542B  |                           
             |                 |     |                             |     |     |                           
p962========p952==============p992   |                             |     |     |                           
 |           |                       |                             |     |     |                           
 |    p142==p152====================p112                           |     |     |                           
 |     |                                                           |     |     |                           
 |     |          p454============================================p564F=p544C=p444
 |     |          p654                                             |     |     |      Digit 4 Layer                   
 |     |           |                                               |     |     |                           
 |     |           |                      p524==p584==============p564F=p544C  |                           
 |     |           |                       |     |                 |     |     |                           
 |    p144========p154====================p124   |                 |     |     |
 |     |           |                             |                 |     |     |
p964===|==========p954==========================p984               |     |     |                           
 |     |                                                           |     |     |
 |     |                p457======================================p567G=p547D=p447                         
 |     |                p657                                       |     |     |      Digit 7 Layer                       
 |     |                 |                                         |     |     |                           
 |     |                 |                            p587==p517==p567G=p547D  |                           
 |     |                 |                             |     |     |     |     |                           
 |    p147==============p157==========================p187   |     |     |     |
 |     |                 |                                   |     |     |     |
p967===|================p957================================p917   |     |     |                           
 |     |                                                           |    p546==p446    Digit 6 Layer
 |     |                                                           |     |
 |     |                                         p521A=p521A=====p561==p541
 |     |                                           |     |                            Digit 1 Layer
 |     |                                   p651==p621H=p621H
 |     |                                     |   p631    |
 |     |                                     |           |
p961===|===================================p951==p991===p921
       |                                     |           |
      p141=================================p151=========p191

=====p256E    \
       |      |  Same node is in two (strong) sets, i.e., 2 sets overlap
=====p256E    /



Golden Nugget Morph, first loop, grid image



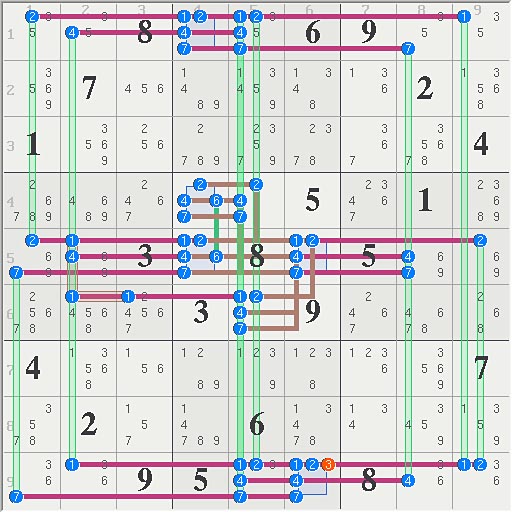
No doubt, Strmckr will now be able to easily solve GN.

Same loop is applicable to
Tungsten rod, and platiumn blonde.

i have been building 9-10+ er rated puzzles based on hidden linked fish (3x same arrangment patterns occuping the same cells.

It seems that we see some of the same structure inside of these monsters, you probably long before me. That is, single digit layers that communicate through common vertical cells. This makes sense because only the single digit layers can use the box constraints.

[StrmCkr]

all i can say is

nicely done...

about time some one grasps how i solve and understands what i can do manually



i just don't have a clue on how to show them with out causing more confusion...

No doubt, Strmckr will now be able to easily solve GN.

already could solve it with that same loop on the original grid

morph it back to the origngal and the elimination pattern also changes with it. showing the same ellimination.

[champagne]

Hi Allan,

First results of a blind "slimfast" program number one on FM loops 1&2.
Program number one is not touching the overall action scope.

Code: Select all

2458  2467  245678 |126789 16789 1678  |24589  1248  3     
2348  2347  1      |23789  3789  5     |6      248   249   
2358  9     2568   |12368  4     1368  |258    7     125   
----------------------------------------------------------
12348 12346 2468   |13678  13678 9     |2347   5     12467
7     12346 2469   |136    5     136   |2349   12346 8     
1389  5     689    |4      13678 2     |379    136   1679 
----------------------------------------------------------
145   8     457    |1367   2     13467 |3457   9     4567 
249   247   3      |5      6789  4678  |1      2468  2467 
6     1247  24579  |13789  13789 13478 |234578 2348  2457 

Actions planned is the clearing of:

2: r4c2
3: r2c1r5c78r6c1r9c467
4: r4c2
6: r1c346r4c9r5c23r8c9

The minimum sets group found has been

N4,2 N5,4 N5,6 N7,7 N8,9 N9,2 N9,5 N9,7
1B2 1B3 1B4 1B6 1B7 1B8
3B1 3B2 3B4 3B6 3B8 3B9
6B1 6B2 6B4 6B6 6B8 6B9

a total of 26 sets.

(The valdity should be checked, what may be you can do. I assume results are correct)

Compared to your loops 1 and 2, we have additional clearings

3: r5c8r6c1r9c46
6: r1c46r4c9r5c2

Your second loop has a total of 35 sets

14 Sets = {136r3 136r7 136c2 136c8 5n46}
21 Links = {136r5 136c4 136c6 3n46 4n2 6n8 7n46 36b1 1b3 1b7 36b9}

But the list of sets I show is not a set/linksets arrangemetns. Some linksets must be added.

In that list are for sure linksets (bearings clearings)

N4,2 N8,9 N9,7 3B1 3B4 3B6 3B8 3B9
6B1 6B2 6B4 6B6 6B9 =13 linksets

So we have 13 potential sets

N5,4 N5,6 N7,7 N9,2 N9,5
1B2 1B3 1B4 1B6 1B7 1B8
3B2 6B8

May be you can make something out of this stuff.
For me, it is still to much.
I will first try "slimfast" program 2, looking for smaller package with reduced actions.
champagne

[Allan Barker]

Hi Champagne,

I will study all this tomorrow.

Don't worry about linksets just yet. They are already determined in a solution, you just have to find them.

It might be nice to have a machine readable code for sets and linksets. I like a binary format (easy to program) like: 81*4 chars, L and S for sets, or additional letters for other meanings.

Code: Select all

R:0000000000S000S000S00SS0SSS00000000000000000SSSS0SSSSS000000000000000000000000000
C:0000000000SSSSSSSSSLLLSSS0000000000000000LLL0LLLL00SS0SSS0SSSS0000000000000000000
N:L000000000LLLLLLLLL00000000000000000000000000000000000000000000000000000000000000
B:0000000000000000SS000000000000000000SSS0SSSS0SSSSSS000000000000000000000000000000


or decide on an ascii format like RCNB for sets rcnb for linksets where you have 3R4, 5c3, etc. The only trouble I might have is the N sets with the comma, we cound decide on Nrc as the format, i.e., N23.

Allan

[Allan Barker]

(The valdity should be checked, what may be you can do. I assume results are correct)

I put your 25 sets into my analyzer but noticed that almost none of your sets have any connection. Did I get the notation wrong?

Code: Select all


EX0a 91 Nodes, Rank -25:
     25 Sets = {4n2 5n46 7n7 8n9 9n257 1b23467 3b124689 6b124689}
     0 Links = {}
     -->

  +-----------------------------------------------------------------------------+
  | 2458    247(6)  24578(6)| 2789(16)789(16) 78(16)  | 24589   248(1)  3       |
  | 248(3)  247(3)  1       | 2789(3) 789(3)  5       | 6       248     249     |
  | 258(3)  9       258(6)  | 28(136) 4       8(136)  | 258     7       25(1)   |
  +-----------------------------------------------------------------------------+
  | 248(13) (12346) 248(6)  | 13678   13678   9       | 247(3)  5       247(16) |
  | 7       24(136) 249(6)  | (136)   5       (136)   | 249(3)  24(136) 8       |
  | 89(13)  5       89(6)   | 4       13678   2       | 79(3)   (136)   79(16)  |
  +-----------------------------------------------------------------------------+
  | 45(1)   8       457     | 17(36)  2       147(36) | (3457)  9       457(6)  |
  | 249     247     3       | 5       789(6)  478(6)  | 1       248(6)  (2467)  |
  | 6       (1247)  24579   | 1789(3) (13789) 1478(3) | (234578 248(3)  2457    |
  +-----------------------------------------------------------------------------+



[champagne]

Hi Champagne,

I will study all this tomorrow.

Don't worry about linksets just yet. They are already determined in a solution, you just have to find them.

It might be nice to have a machine readable code for sets and linksets. I like a binary format (easy to program) like: 81*4 chars, L and S for sets, or additional letters for other meanings.

Code: Select all

R:0000000000S000S000S00SS0SSS00000000000000000SSSS0SSSSS000000000000000000000000000
C:0000000000SSSSSSSSSLLLSSS0000000000000000LLL0LLLL00SS0SSS0SSSS0000000000000000000
N:L000000000LLLLLLLLL00000000000000000000000000000000000000000000000000000000000000
B:0000000000000000SS000000000000000000SSS0SSSS0SSSSSS000000000000000000000000000000


or decide on an ascii format like RCNB for sets rcnb for linksets where you have 3R4, 5c3, etc. The only trouble I might have is the N sets with the comma, we cound decide on Nrc as the format, i.e., N23.

Allan

Don'tworry....

I don't. I wanted just to point that in the process leading to the MGS, unless I was wrong having a quick look to the MGS, some sets are alone, which should not happen in your set/linkset analysis. But I have to check carefully the results.

I suggest

Code: Select all

R:..........S...S...S..SS.SSS.................SSSS.SSSSS...........................
C:..........SSSSSSSSSLLLSSS................LLL.LLLL..SS.SSS.SSSS...................
N:L.........LLLLLLLLL..............................................................
B:................SS..................SSS.SSSS.SSSSSS..............................
  1        2        3        4        5        6        7        8        9       


N sets with the comma, ...
I tried in that first entry in your field, to avoid any confusion. As we are often speaking of 81 nodes, I was sure N2,3 could not be confused with node number 23. But I can rally any convention.

champagne

[champagne]

(The valdity should be checked, what may be you can do. I assume results are correct)

I put your 25 sets into my analyzer but noticed that almost none of your sets have any connection. Did I get the notation wrong?
[/code]

Ok we came to the same conclusion. If there is no bug in the process, this would mean that connecting linksets bring nothing more.

to be clarified

champagne