The New Sudoku Players' Forum

[champagne]

Thanks very much ALLAN,

I would not say it's quite clear now, but at least the 14 linksets span is OK.

On the pure logic side, it's not complex. I'll see why it has not been found by my solver thru AIC's nets.

The new "key sentence" (for me) is here

Two of the triplets must be occupied thus 13 of the 14 linksets are guaranteed to be occupied, and the rank everywhere must always be 1 or lower

champagne

[champagne]

Hi Allan,

I checked the logic. It could be summarized that way:

If all pairs solving a two nods set are solving another 2 nods set, the other 2 nods set is saturated.

1) This is not included in my rules,
2) My set of rules can not solve that pattern, but such a rule coul surely be added

3) Adding such a rule (you can define hundreds of them) is not a very exiting, it is too specific (unless proven to appear frequently in the area where my solver is not efficient).


I stick to my first idea to try to add your rules.



4) strmckr has here a logic statement he was looking for.


edit:

Even if I added such rules, I have no evidence that there is an AIC net corresponding to that case in the limits of my scope.

The situation described by Allan is "relatively simple" to handle in a kind of T&E mode, I have still to find how it could be expressed in AIC mode.

[StrmCkr]

correct

edit.

think of it as a grouped Fish ocucpying the same dimenisioal restrictions.

ie
3 columns 3 rows x 3 digits confined to that same space.

my
understanding puts these as some kind of hidden restriction pattern.

i have been playing with the concepts via building a puzzle
with 3 fish patterns layered as one unit.
seems to work.


the digits 157 in tungstun rod form the same thing.

[champagne]

cancelled

[champagne]

Hi Allan,

I worked on loop 2.

1) I find an overall rank 1 if I apply your rule "one must be true".
I hope this is corrrect, but the last step, finding rank 0 sets requires skills I don't have.

2) I looked for another nice simple logic to cover that case, but up to now, I failed (I thought I had one, but I mad a mistake).

May be you have something to suggest.

champagne

ps: BTW do you have an order of magnitude of the processing time to solve such a puzzle with your rules and your process. What I am forecasting up to now is not good at all compared to what I got for Golden Nugget (about 60 seconds).

[Allan Barker]

I worked on loop 2.

1) I find an overall rank 1 if I apply your rule "one must be true".
I hope this is correct, but the last step, finding rank 0 sets requires skills I don't have.

You are almost getting ahead of me, this one is going to be a beauty. I'm just about to the last step but I'll tell you some clues I have found.

1. There are 2 or three groups of linksets. Under Links below, either group of linksets in paren() can be removed and the logic is still covered.

Code: Select all

42 Nodes, Rank 7
     14 Sets = {136r3 136r7 136c2 136c8 5n46}
     15+(6) Links = {(136c4 136c6) 136r5 (3n46 7n46) 4n2 6n8 36b1 1b3 1b7 36b9}

One case makes pure rank 1 logic with no triplets, just plain rank 1 logic, (no eliminations)

Code: Select all

42 Nodes, Rank 1
     14 Sets = {136r3 136r7 136c2 136c8 5n46}
     15 Links = { 136r5 (3n46 7n46) 4n2 6n8 36b1 1b3 1b7 36b9}

Another case makes logic just like the first loop, with the two rank 0 cell linksets.

Code: Select all

42 Nodes, Rank 3
     14 Sets = {136r3 136r7 136c2 136c8 5n46}
     17 Links = {(136c4 136c6) 136r5  4n2 6n8 36b1 1b3 1b7 36b9}

When all linksets are combined they make 2 more SIS, + the asymmetry of digit layer 1 leads to the extra rank 0 sets. I will try to post later and we can discuss. You might want the look at the Tungsten Rod, since it is similar to loop1 but with 1 bi-value set.

[Allan Barker]

i have been playing with the concepts via building a puzzle
with 3 fish patterns layered as one unit.
seems to work.
the digits 157 in tungstun rod form the same thing.

Yes, I see that Tungsten Rod is all very similar. Just took an initial look, I can't quite make the full layer digit 5 work out but I found this baby SK Loop while looking. It is all the same principles as the others. However, this example has one small bi-value set in set 5r6. The four triplets make the logic to rank 1 and two sets overlap for eliminations, not rank 0.

Code: Select all

TR01= 28 Nodes, Rank 4:
     9 Sets = {17r2 167r4 17r8 56n6}
     13 Links = {1c367 7c367 2n5 4n3457 8n4 5b5}
     Elim. --> (4n4*5b5) => r4c4<>5, (4n5*5b5) => r4c5<>5

  +-----------------------------------------------------------------------------+
  | 34589   4568    34689   | 12356   123569  15689   | 24      1389    7       |
  | 3589    2       389(7)  | 4       359(17) 589(17) | 389(1)  6       389     |
  | 1       4678    346789  | 2367    23679   6789    | 5       389     24      |
  +-----------------------------------------------------------------------------+
  | 358     9       38(17)  | 35(167) 35(167) 2       | 38(17)  4       358     |
  | 2345    1457    12347   | 8       13457   (157)   | 6       13579   2359    |
  | 6       14578   123478  | 9       13457   (157)   | 12378   13578   2358    |
  +-----------------------------------------------------------------------------+
  | 2489    1468    5       | 1267    12679   3       | 4789    789     4689    |
  | 49      3       469(1)  | 56(17)  8       569(17) | 49(7)   2       4569    |
  | 7       68      2689    | 256     2569    4       | 389     3589    1       |
  +-----------------------------------------------------------------------------+

p446==p456
 |     |                                                                     
 |     |    p831======================================p861==============p841 
 |     |     |                                         |                 |   
p441==p451==p431A=p431A============p471C=p471C         |                 |
 |     |           |                 |     |           |                 |
 |     |           |                 |    p271==p251==p261               |   
 |     |           |                 |           |     |                 |   
 |     |           |                 |           |    p561==p567==p565   |
 |     |           |                 |           |     |     |     |     |
 |     |           |                 |           |    p661==p667==p665   |   
 |     |           |                 |           |           |           |
p447==p457========p437B=p437B=p477D=p477D        |           |           |   
                         |     |                 |           |           |   
                        p237===|================p257========p267         |   
                               |                             |           |   
                              p877==========================p867========p847 
 
[===p123===] node rcn notation
[ p123A ] letters for same node in 2 or more sets/linkset (same letter)
[  = ] = strong set
[  | ] = weak set (can be strong set in puzzle)

[champagne]

You might want the look at the Tungsten Rod, since it is similar to loop1 but with 1 bi-value set.

Not really, I would like to swim.

I have not yet the skill to "reduce the count".

May-be you misunderstood me. When I am speaking of rank1, it is reducing the count in Loop 2 as you did in loop 1 starting from rank 7 (your diagram)

The elimination can also be described in terms of rank and zones. All six nodes in sets n54 and n56 make triplets (each node is in 2 linksets). Two of the triplets must be occupied thus 13 of the 14 linksets are guaranteed to be occupied, and the rank everywhere must always be 1

but then, (if I am right having reduced the count by 6), I have still to find rank0 sets

[ronk]

Code: Select all

TR01= 28 Nodes, Rank 4:
     9 Sets = {17r2 167r4 17r8 56n6}
     13 Links = {1c367 7c367 2n5 4n3457 8n4 5b5}
     Elim. --> (4n4*5b5) => r4c4<>5, (4n5*5b5) => r4c5<>5

Hi Allan, I've not been following closely lately, so have fallen way behind. If my question is simplistic, I apologize.

I don't understand the need for linksets 4n37. If linksets 4n37 are dropped, the rank is 2. Moreover, I see no set triplets to complicate this example.

I've learned from single-digit constraint sets (fish) that if one has N sets (base sets) and N+2 linksets (cover sets), that an elimination must be "triply covered." Your eliminations are merely doubly covered at the linkset triplets.

From that point of view, how do you justify the eliminations

[Allan Barker]

May-be you misunderstood me. When I am speaking of rank1, it is reducing the count in Loop 2 as you did in loop 1 starting from rank 7 (your diagram)
but then, (if I am right having reduced the count by 6), I have still to find rank0 sets

I did miss the fact you were going all the way from rank 7 to rank 1 because I started in another direction using the two different cover sets. Often, more than one way will work. Then next step to rank 0 is the first of its kind and I'm only about half way. When it's done, I will put this one on the website, I think it needs deep water.

[champagne]

Then next step to rank 0 is the first of its kind and I'm only about half way. When it's done, I will put this one on the website, I think it needs deep water.

It sounds like what I experienced when I started fighting against hardest puzzles.

The solver found clearings, but the tracking back was bugged and I sometimes had looping explanations, explaining nothing.

When the process will be ok, don't forget to describe precisely how the solver works to find the final rank.

champagne

[Allan Barker]

Hi Ronk.

Hi Allan, I've not been following closely lately, so have fallen way behind. If my question is simplistic, I apologize.

Fate Morgana seems to have produced on some rather unique logic, particulary the loop 2, so we are probably all a bit behind here.

I don't understand the need for linksets 4n37. If linksets 4n37 are dropped, the rank is 2. Moreover, I see no set triplets to complicate this example.

I've learned from single-digit constraint sets (fish) that if one has N sets (base sets) and N+2 linksets (cover sets), that an elimination must be "triply covered." Your eliminations are merely doubly covered at the linkset triplets. From that point of view, how do you justify the eliminations?

This is a very good question because part of the answer relates directly to what's in the last couple of posts about FM. Everything is correct including not needing linksets 4n37 as they are not required to cover the sets. However, they are what cause the eliminations. Normally, adding extra linksets will do nothing (if all sets are already covered). On fairly rare occasions, they can make triplets that can lower the rank perhaps of only in part of the logic and result in eliminations.

The loop 2 of FM is a more complicated example, which can have two configurations, one with 4 extra and one with 6 extra linksets not required to cover the logic.

The next question might be exactly how do they lower the rank in this case? That also relates to the FM logic so I will try to post something tomorrow, as it is already tomorrow! The short answer is that extra linksets can add extra constraints to a problem.

[Allan Barker]

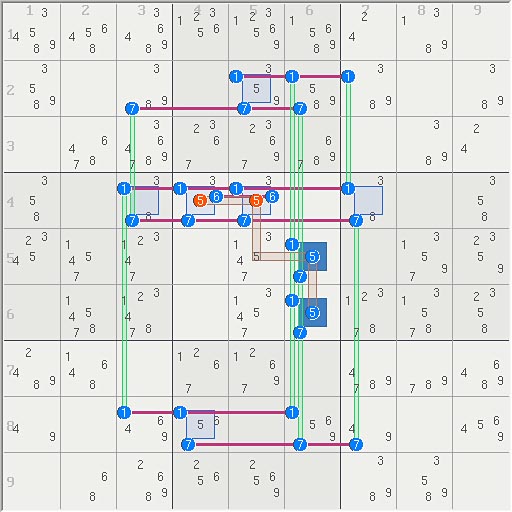
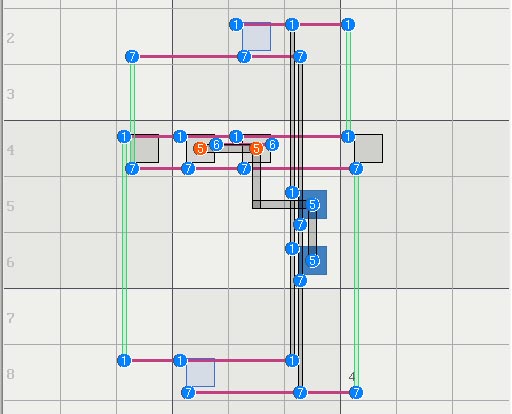
When the process will be ok, don't forget to describe precisely how the solver works to find the final rank.

Set Solver

The solver was initially designed to explore second order logic. It finds logic by adding one full set at a time to a 'path' of sets. It is free to choose any set without restriction so the 'path' can be any shape. Sets means the primary Sudoku constraints with 81 row, column, cell, and box sets each for a total of 324 sets. There is no T&E. It implements only one logic rule, the Sudoku rule itself, i.e., every set must have exactly one member.

It uses a permutation analyzer to analyze each step or logic block along a path. The same analyzer provides logic simulation while editing or building logic by hand. Given a matrix:

Code: Select all

                        Nodes
             +------------------------
             | 00101011000101011101101
Permutations | 11101000111001010111010
             | 00111010101010101101010


An elimination is any column with all 0s and, an assignment is any column with all 1s. The table is built one full set at a time so the solver is aware of the set structure, thereby fully implementing the Sudoku rule. Linksets are "recognized" later thus the solver naturally discovers the use of cover sets, the lack of them as in a broken wing, or the use of multiple covers like in FM/TR. The solver finds anything based on the Sudoku rule, but currently knows nothing about uniqueness.

Permutations are not used for search but only to express a logic equation for the logic, multiple permutations are equivalent to logical or'ing at individual nodes. The advantage is that the solver has 100% of all information about the logic. Below is an X wing that eliminates two candidates:

Code: Select all

             Nodes
             +----------
Permutations | 0110  00
             | 1001  00
                     ^^-- elimination

This approach is good for making a Sudoku simulator or analyzer, making it easy to hand build logic and ask what-if questions, or do things like assuming nodes are true or false to see the logical consequences.

Speed.

Direct comparison is not so easy. The set approach can solve say GN in a few seconds if run as a grid solver, finding a logical solution but not extracting the individual logic for each elimination. I am using register bits all the way, without which I would probably be the same or slower than your times. My guess is the amount of required operations (you vs. me) is roughly similar. Great monsters are usually solved interactively and the user can explore various options or solution paths. The slowest part of the process is having too much fun.

Next Step?

The set logic rules, like rank 0 to N, triplets, etc, are derived to explain what comes out of the solver. Now the question would be how to make a solver based on these set logic rules, which have been shown to cover most everything. Such a solver might be very efficient especially with something like tagging if possible. It would be interesting.

Edit: shift "^^-- elimination" to its correct position in the code block

[champagne]

Hi Allan,

This was for me a good post (and the confirmation that I was not on the right way with my preliminary thinking’s about how to implement your rules).

Speed.

Direct comparison is not so easy. The set approach can solve say GN in a few seconds if run as a grid solver, finding a logical solution but not extracting the individual logic for each elimination. I am using register bits all the way, without which I would probably be the same or slower than your times.

Believe me, this put the target at a very high level. You can read here and there of processes lasting hours, sometimes failing due to “memory limitations”.

My experience is that if you have a performing process to locate solving patterns, performance in backtracking process is not an issue.

Regarding processing time in my solver, ir is highly depending on the number of tags processed (levels) and on the number of cycles done.



More important , a need for clarification regarding your wording. I mix your text to come to the easiest situation

It uses a permutation analyzer to analyze each step or logic block along a path. The same analyzer provides logic simulation while editing or building logic by hand.

Below is an X wing that eliminates two candidates:

Code: Select all

            Nodes
             +----------
Permutations | 0110  00
             | 1001  00
                                          ^^-- elimination

An elimination is any column with all 0s and, an assignment is any column with all 1s. The table is built one full set at a time so the solver is aware of the set structure, thereby fully implementing the Sudoku rule. Linksets are "recognized" later thus the solver naturally discovers the use of cover sets, the lack of them as in a broken wing, or the use of multiple covers like in FM/TR. The solver finds anything based on the Sudoku rule, but currently knows nothing about uniqueness.

Let say a digit 2 map

Code: Select all

2 - -  2 - -
- - -  - - -
- - -  - - -

2 - -  2 - -
- - -  2 - -
2 - -  - - -

And no more “2” (no matter whether you can find it in a puzzle)


1) You write the matrix is a “node matrix” so here the first line should be the “digit 2” map.

2) Two permutations will affect this set : permuting horizontal band 1 and 2; permuting vertical band 1 and 2.

If the matrix refers to “sets” r12 and r42, they should always be occupied.
If the matrix is a “digit 2” map, p142 and p612 are defined in the first line and will be “0” in any other place. Then can be cleared.

If this second point is the right answer, it makes sense.

champagne

[Allan Barker]

Tungsten Rod Baby SK Loop Elimination in Detail

This is a full description of the Tungsten Rod elimination discussed above, based on rank rules.

The triplet rule is: An occupied triplet lowers the global rank by 1, an unoccupied triplet lowers the rank in its 'set' branch by 1. The true (or resultant) rank will be the higher of the two states. Lower is relative to whatever rank before considering the triplet.

Consider the TR loop logic with the 'extra' linksets n43 and n46, which are not cover sets but do cause the elimination by adding additional constraints. The extra linksets make 4 symmetric triplets in 2 row sets, 1r4 and 7r4, which means that two triplets must always be unoccupied with two configurations: (r4c7<>1 and r4c3<>7) or (r4c7<>7 and r4c3<>1). This makes for a rather easy solution that does not depend on the global rank.

The two unoccupied triplets will lower the rank in their set-branches. The easy way to see the set branches is to assume that r4c7<>1 and r4c3<>7 i.e., assume that triplets B=0 and C=0, as marked in the diagram.

Code: Select all

Tungsten Rod baby SK loop:
Full logic.

7r5c6=5r5c6==============================================1r5c6
  |     |                                                  |
7r6c6=5r6c6==============================================1r6c6
  |                                                        |
7r8c6=======7r8c7==================================7r8c4   |
  |           |                                      |     |
  |           |                              1r8c3=1r8c4=1r8c6
  |           |                                |           |
  |           |           6r4c4=6r4c5          |           |
  |           |             |     |            |           |
  |         7r4c7D=7r4c7D=7r4c4=7r4c5=7r4c3B===|===========|===============7r4c3B
  |                  |      |     |     |      |           |                 |
  |                1r4c7C=1r4c4=1r4c5=1r4c3A=1r4c3A========|=========1r4c7C  |
  |                                                        |           |     |
  |                                                      1r2c6=1r2c5=1r2c7   |
  |                                                              |           |
7r2c6==========================================================7r2c5=======7r2c3


Assume triplets B=0, C=0:
Note: A and D are no longer triplets, and 2 linksets can also be removed


       5b5         5n5   5n4  (linksets)
        .           .     .
7r5c6=5r5c6===============================1r5c6         +
  |     |                                   |           |
7r6c6=5r6c6===============================1r6c6         |    7 sets
  |     |                                   |           |    8 cover sets
7r8c6=======7r8c7===================7r8c4   |           |    RANK 1
  |     |     |                       |     |           |
  |     +-----|---->X---->X   1r8c3=1r8c4=1r8c6     UPPER (SET) 
  |           |     |     |     |           |         BRANCH
  |           |   6r4c5=6r4c4   |           |           |
  |           |     |     |     |           |           |
  |      (D)7r4c7=7r4c5=7r4c4   |           |           |
  |                 |     |     |           |           |
  |               1r4c5=1r4c4=1r4c3(A)      |           |
  |                                         |           +
..................................................................
  |                                         |           |
  |                                       1r2c6=1r2c5=1r2c7
  |                                               |
7r2c6===========================================7r2c5======7r2c3
                                                             |


The upper branch has 7 sets, 8 linksets, and is rank 1. It contains cover sets 5b5, 5n5, and 5n4, which overlap to eliminate the 2 candidates marked X. Note that sets 1r2 and 7r2 are not in the rank 1 zone. The second solution assumes that triplets A=0 and D=0 and then then sets 1r8 and 7r8 would not be in the rank zone. The real rank 0 zone has all sets except sets {1r2 7r2 1r8 7r8, plus thr required cover sets.

The image below shows the rank 1 region with black linksets.