The New Sudoku Players' Forum

[SpAce]

Hi eleven,

I don't quite understand your method.

I'm more than happy to help, but I'm not sure I understand what you're asking/saying.

In the "first eliminations" picture you can color 9r1c1 green,

Yes, indeed. I didn't yet do that because I wanted to focus on those eliminations and the super-candidates causing them.

then (single in box 4) 9r4c3, 1r5c5 and so on, until you have all the greens in "more eliminations".

Exactly.

Here 5r9c2 is the only remaining 5 in box 7

Indeed it is, although it seems that I hadn't yet colored the 5b7p6 light red as I should have. 5r9c2 is also the only remaining 5 in column 2, so either way it's a "hidden single" within the Dark parity. But, it hasn't yet been colored as such (green or blue) so it can't be used as such either. Normally it would be colored dark green (super-candidate) like the other "singles" but because it's already dark red (sub-candidate) it will be insta-promoted into dark blue (par-candidate).

A par-candidate is basically both a super and a sub at the same time. It's a subtle but significant difference, because unlike mere supers (which can only turn their peers into subs) the pars can also turn conjugate candidates into opposite pars which can do the same and so on. So, par-candidates are much better at spreading the coloring and causing eliminations, among other things. This is a big difference between GEM and simpler coloring methods that don't track the different grades. Those other methods have to also remember exactly where they started the coloring if they're using the same color for all "placements" and are following weak links.

In this example the par promotion doesn't make any difference though, because the 5r9c2 doesn't have any conjugates to turn, so it would work the same way if colored green. However, if you look at the "solution" to the other puzzle in my previous post, you'll see some more promoted par-candidates that actually got some extra eliminations that way (if I remember correctly).

, and the 8r9c3 the only 8.

Yes, though it's in the opposite (Light) parity. We have to be careful to avoid mixing the two opposite contexts. It's especially easy to get confused when cells have mixed subs and you're looking for a locked set, for example. Only the reds of the opposite parity can be considered eliminated.

This already gives all eliminations in that picture.

It should. What exactly is your question? In the next picture the 5r9c2 has been turned into a par-candidate which has eliminated the 8r9c2 giving us the 8r9c3 placement.

[Mauriès Robert]

TDP Part 4
See TDP Theory (part 4) which replaces the original text of this post.
Robert

[Mauriès Robert]

Hi SpAce and Eleven,

I looked as closely as I could at SpAce's article on GEM and I think I understood how it works. If GEM and TDP do the same thing because they are techniques that operate two networks, one of which is true and the other is false, but in practice they are different approaches on several points:
1) TDP only uses basic techniques (TB), while GEM uses advanced techniques. That is why the TDP considers the search for incompatility as a technique..
2) TDP does not use sub-colours to distinguish between weak and strong links, nor does it use these concepts, whereas GEM builds the network of strong links on which everything is based.
3) TDP is less cumbersome to handle since only les techniques de base is used and it has been designed for sudokists who have difficulty with advanced techniques.

I have just posted part 4 of TDP and I remain at your disposal to discuss.
I still have to do a part on uniqueness, because on my website I am also interested in puzzles with several solutions.

Sincerely
Robert

[SpAce]

Hi Robert,

Just a few quick comments for now:

I looked as closely as I could at SpAce's article on GEM and I think I understood how it works. If GEM and TDP do the same thing because they are techniques that operate two networks, one of which is true and the other is false, but in practice they are different approaches on several points:

I agree that they have several differences, but not necessarily the ones you listed.

1) TDP only uses basic techniques (TB), while GEM uses advanced techniques.

GEM doesn't mandate or restrict the use of any techniques. It's just a coloring framework that supports using as simple or as complex nodes as you want. Obviously skilled players can do more with GEM because they can see more easily advanced patterns that can be used to extend the coloring. One is still free to use basic techniques only, but obviously the coloring can't advance as much with them. It just means that you need to either use a different seed or nested coloring earlier -- just like with TDP.

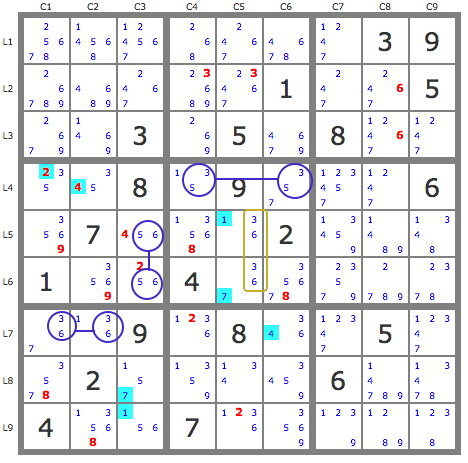
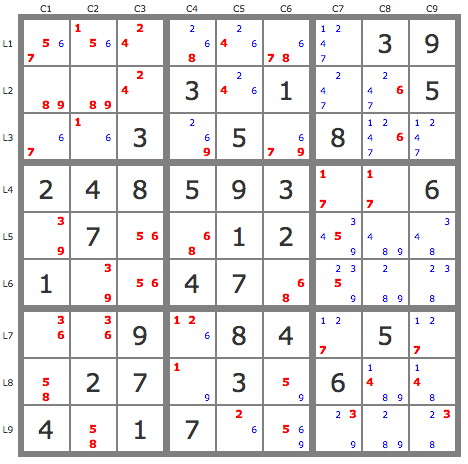
Where in my GEM demo did I use more advanced techniques than you? I remember only one place and it was the UR I used to extend the coloring. The nice thing about GEM is that such patterns become visible once you get used to the coloring. I don't think there's any way that UR could have been spotted with the simpler TDP coloring. I don't think many of the locked sets or grouped nodes could have been either. So, I think it's more correct to say that GEM makes it much easier to use advanced (or even basic) techniques within the coloring, but it doesn't require it any more than TDP.

This explains why TDP considers disability research as a technique.

Could be, but I think it's more of a philosophical difference too. I'll get back to this later, when I find time to answer your earlier comments about T&E. Anyway, there's nothing in GEM that prevents using it to look for direct contradictions if one wishes. It's just not much fun.

2) TDP does not use sub-colours to distinguish between weak and strong links, nor does it use these concepts,

That's misleading. Of course it uses those concepts even if doesn't state it explicitly. All the singles in your P(E) sets are there because of following alternating weak and strong links from the starting candidates. Similarly, all your contradictions are found following those links as well. How else do they happen? By magic?

GEM just makes all of that explicit, which in turn makes it much easier to follow the coloring and the reasoning behind any eliminations or contradictions found. That's why any deductions found via GEM are also possible to trace and write as AICs or nets. TDP hides all those details, which makes it seem simpler, but it actually makes the deductions much harder to spot and to understand.

As a result, one clear weakness of TDP seems to be that it lacks a way to document the solution steps in a way that's easily followed without doing it yourself or running it through a software solver. For example, I don't really understand your solution here. All the other solutions are easily verified just by looking at the grid and the provided AIC or fish.

whereas GEM builds the network of strong links on which everything is based.

This is not a real difference either, if you refer to the initial par cluster. You could use GEM just like TDP without building it. In that case only the starting pair would be special -- just like it's in TDP (because you have to know where you started). All the other "singles" would be super-candidates. GEM would still work without the par-candidates but it would be weaker. Btw, this is exactly how GEM is used if the seeding pair is not conjugate (i.e. they have an OR relationship instead of XOR). In that case there are no initial par candidates at all. (Similarly, coloring the sub-candidates can be skipped as well. With just a starting pair and super-candidates GEM would be exactly the same as the TDP coloring.)

3) TDP is less cumbersome to handle

That is a matter of opinion. Obviously I see it the other way around. I don't find GEM cumbersome at all, because it visualizes everything very clearly once you get used to it. The coloring is straight-forward and less error-prone to build manually, for example because the sub-candidates make it much easier to see where the next super-candidates will be. In TDP it's a lot harder to place all those singles in each branch, and I don't know how you could see any group links and locked sets and stuff at all. If I tried to do that manually I'd probably miss a lot of things that are obvious with GEM. The only viable way to use TDP, at least for me, would be to let a computer generate those branches.

since only TB is used and it has been designed for sudokists who have difficulty with advanced techniques.

There's nothing in GEM that prevents it from being used like TDP and with any technique sets one wishes. As far as I see, it's a superset of TDP coloring, so if you strip out enough features (mainly the par- and sub-candidates) it becomes TDP coloring. Maybe such apparent simplicity works better for some people, but I know it wouldn't work for me.

I have just posted part 4 of TDP and I remain at your disposal to discuss.

Thanks, I'll get back to that. At a first glance it kind of looks like the nested coloring I did at the end of the GEM demonstration. Btw, you've missed a hidden triple/naked quad in box 7.

[Mauriès Robert]

Hi SpAce,

Thank you for all these remarks. I think that the habit of using a technique does a lot in the appreciation we have of it.
If I have understood you correctly, in your opinion TDP is a special case of GEM. Of which act!
In box B7, it's an oversight on my part but not important for what I wanted to show, I corrected.

Sincerely
Robert

[SpAce]

Thank you for all these remarks. I think that the habit of using a technique does a lot in the appreciation we have of it.

Of course, and I realize it affects my judgment too. Still, I'm always looking for ways to improve my tools and methods, so I'm definitely keeping an open mind.

It's just pretty hard to convince me that a better coloring method than GEM exists, because it was a perfect fit for me right away. If David hadn't already invented it, I probably would have, because I was thinking of something exactly like it when I found it. That's why I adopted it immediately and created my own ways to use it (first on paper and then on Hodoku). That doesn't stop me from switching to something else if something clearly better comes around. Somehow I doubt it.

If I have understood you correctly, in your opinion TDP is a special case of GEM.

I should have specified that I only meant the coloring part (corrected now). Then it's not an opinion but an obvious fact. That said, GEM is just a coloring framework so it makes no sense to compare it to any other features of TDP (though I'm pretty sure GEM supports them all). I don't even claim to understand all the other features of TDP so far, because they're hidden under such heavy theory. Somehow I'm thinking that those concepts are much simpler than what your complicated mathematical presentation makes them seem. That's why I find this kind of funny:

3) TDP is less cumbersome to handle since only basic techniques are used and it has been designed for sudokists who have difficulty with advanced techniques.

Well, I don't have difficulties with advanced techniques, but I surely have difficulties understanding parts of your TDP presentation (especially parts 1 and 2, which should be the easiest)! It's not a language problem, as I've tried to read them in French too and I don't think I would understand them any better even if my French skills were better.

In box B7, it's an oversight on my part but not important for what I wanted to show, I corrected.

I understand. However, did you notice that it would allow you to eliminate 5r8c3 and 5r9c89 via normal coloring? That might simplify things a bit. Also, since you don't mind contradictions, you could easily see that P(3r3c4).P(4r9c89) is invalid giving you +3r3c3, after which it's trivial. But yeah, I know it's not what you wanted to demonstrate with this example.

[Mauriès Robert]

TDP Part 5
See TDP Theory (part 5) which replaces the original text of this post.
Robert

[Mauriès Robert]

Hi SpAce,

Concerning the definition (TDP part1) for which you also asked me, there was one word missing, it was necessary to read "closed set".
So I reworded the definition in the hope that it would be more understandable.

A set of candidates E1={B1j, j=1.2,...} is a closed set contained in P'(E) when a candidate of each component E1i of E1 is necessarily a candidate belonging to P'(E).

The term necessarily means here "if we want to respect the rules of sudoku" in the ongoing construction of the anti-track (or track).

I have taken up some of the texts in this section in the hope of improving their understanding. Here.

Sincerely
Robert

[SpAce]

Hi Robert,

I agree that we should continue this discussion here. So, I'll repeat my original question below for clarity.

Definition:
An anti-track P'(E) is said to contain a set of candidates E1={B1j, j=1,2,...} when a candidate of each component E1i of E1 is necessarily a candidate belonging to P'(E).

What do you mean by "necessarily"? If the starting condition is invalid then there's no such concept, as any candidate can be forced to become part of the resulting set. Only valid tracks have definite members. Invalid tracks can have anything. So, unless you know beforehand that your P'(E) track is valid, you can't have a definite list of candidates that belong to it.

Concerning the definition (TDP part1) for which you also asked me, there was one word missing, it was necessary to read "closed set".
So I reworded the definition in the hope that it would be more understandable.

A set of candidates E1={B1j, j=1.2,...} is a closed set contained in P'(E) when a candidate of each component E1i of E1 is necessarily a candidate belonging to P'(E).

The term necessarily means here "if we want to respect the rules of sudoku" in the ongoing construction of the anti-track (or track).

I still don't get it. There is no closed set of candidates in an invalid track. It can contain anything depending on the routes you take building that track. That's exactly why invalid members of strongly linked sets can be used to prove any verity, because they can always be made to agree (locally) with valid candidates (sometimes with considerable difficulty but it can always be done).

Valid candidates can't lie, so they can only generate valid tracks with definite sets of candidates if the puzzle has at least one solution. On the other hand, invalid candidates can and do lie, but that's ok, because if we know that at least one of our (strongly linked) starting options must be valid, then we know that anything they all can agree upon must be valid as well. Those agreements are verities.

So, what exactly do you mean by "closed set" and "necessarily"? To me it still implies that any track, valid or not, somehow generates a fixed set of candidates every time. That's simply not true for invalid tracks, because the qualification of "respecting the rules of sudoku" doesn't really apply to them. With an invalid starting condition you can only respect those rules locally, but there's always a global contradiction somewhere (not in a fixed place) which generates different sets of candidates depending on which routes you travel first. Every candidate in that set, including the starting candidate(s), can be switched to something else by respecting sudoku rules locally, so there's nothing "closed" about it. Invalid candidates do not only lie but they can change their stories (and even identities) as well.

[Mauriès Robert]

Hi SpAce,

I understand your questioning, I have often had this type of discussion in France with sudoku theorists (mathematicians in general!).

By definition, we build an anti-track (or a track) assuming that we have the right to use the sudoku rule, and as long as we have not encountered an incompatibility the construction is legal. In a way, we behave as if the anti-track (or track) were valid. This explains why we consider this type of definition (closed set contained in the anti-track or track) until we know if the anti-track or (track) is valid or invalid.

The best way to make you understand what I mean is to give an example.

On the Nugget puzzle : .......39.....1..5..3.5.8....8.9...6.7...2...1..4.......9.8..5..2....6..4..7.....
I choose E={63r5c5, 63r6c5} and I build P'(E).
Sets E1={35r4c4, 35r4c6}, E2{56r5c3, 56r6c3} and E3{36r7c1, 36r7c2} are all closed sets contained in P'(E).
At this stage it is not known whether P'(E) is invalid or valid, but P'(E) is made up of the candidates marked in blue and necessarily 2 candidates (but I don't know which ones) from each of the closed sets E1, E2, etc...
At this stage of the construction of P'(E), if you do not accept "closed set" and "necessarily" in the definition then you conclude that P'(E) is invalid when you do not know it.



To fully understand what an anti-track (or track) is, you must actually place the candidates of the anti-track (or track) on the puzzle and see what it looks like. If I do it here, we get the following puzzle on which we see the closed sets E2 and E3, and the candidates placed from E1.

[SpAce]

Hi Robert,

I understand your questioning, I have often had this type of discussion in France with sudoku theorists (mathematicians in general!).

Well, I'm not a sudoku theorist but rather a pragmatist with a pretty good idea of what works in practice and why. I'm certainly no mathematician, which is why I'm not the biggest fan of your mathematical presentation. It's related to this (which you wrote in the other thread):

You say that TDP is complex

No. I've never said that. I've rather said that you've made relatively simple concepts seem more complicated than they are with your "rigorous" way of presenting them. Btw, to be truly rigorous, shouldn't your theorems be accompanied by formal proofs as well? (I'm glad they aren't.)

By definition, we build an anti-track (or a track) assuming that we have the right to use the sudoku rule, and as long as we have not encountered an incompatibility the construction is legal.

The construction is actually legal even if you encounter an incompatibility. There's no rule that says you must stop there, or any guarantee that you even notice the incompatibility immediately. You can still use the sudoku rule locally (you just have a choice of where and how) and advance the coloring to produce a completely different set of candidates. That's how AICs work because they don't remember anything from previous states. That's why the same cell can have two different values within a single AIC, or in other words the same candidate can be considered both on and off. Obviously it tells something about the validity of that route, but it's a perfectly legal construction and capable of proving what we want nonetheless.

In a way, we behave as if the anti-track (or track) were valid.

Exactly. But since one of them isn't, there's no (globally) closed set of candidates for both of them, and because we don't know which track is valid (and actually has a closed set) we should rather not assume anything about it at all. That's my whole point.

This explains why we consider this type of definition (closed set contained in the anti-track or track) until we know if the anti-track or (track) is valid or invalid. The best way to make you understand what I mean is to give an example.

I understand what you mean just fine. I just don't agree with it. Unless you restrict the cells to a subset of the puzzle, no closed set of candidates exists for an invalid track. It can be easily seen with both of your examples: the Cigarette (which you deleted for some reason) and the Nugget. If the coloring is continued beyond your chosen cells, it will produce a different set of candidates for the P'(E) track in both cases.

So, your rule only works very locally, which means it's not a valid general rule. You should state that to avoid this kind of confusion. In fact, the whole rule is unnecessary because we can use any set of candidates produced by an invalid track to prove what we want. They don't have to be "necessarily" generated or form "closed sets" at all, and that's good for us, because those concepts are not globally valid for invalid tracks anyway.

At this stage of P'(E) construction, if you do not accept the "closed set" and "necessarily" then you conclude that P'(E) is invalid when you do not know it.

The important qualification being "at this stage". If the construction is continued, things change rapidly.

To fully understand what an anti-track (or track) is, you must actually place the candidates of the anti-track (or track) on the puzzle and see what it looks like.

No, I don't have to do that. That's why I use GEM. Believe me, I understand what you're doing just fine because the underlying concepts are not at all different from what I do. I just don't agree with your "closed set" idea because it doesn't work globally nor is it necessary.

Btw, the way you present your solutions without showing the chains leading to your candidate sets is ambiguous because of this (globally) false "closed set" idea. It doesn't account for the fact that different routes would produce different sets for the invalid tracks. What you're showing is just one possibility, and without telling how you got there, it's not necessarily easily verifiable (at least in more complex cases than we've seen so far). That's why we write chains to avoid such ambiguity.

[Mauriès Robert]

Hi SpAce,

Btw, to be truly rigorous, shouldn't your theorems be accompanied by formal proofs as well? (I'm glad they aren't.)

All my theorems are demonstrated at least in my French document. The theorem 1 TDP part 1 is demonstrated here, I don't understand your criticism!

...la cigarette (que vous avez effacée pour une raison quelconque)

I finally deleted the cigarette so as not to make the message heavier, Nugget being enough to explain my opinion. I do the same thing with cigarettes without any problem.

The important qualification being "at this stage". If the construction is continued, things change rapidly.

Explain yourself, because I don't see how the development of P'(E) will challenge what I did?

I just don't agree with your "closed set" idea because it doesn't work globally nor is it necessary.

I believe we will not be able to agree, unless I can convince you one day through examples!

No, I don't have to do that

I never do that either, here it's only to show you the anti-track as the image of a sub-puzzle of the starting puzzle.

It doesn't account for the fact that different routes would produce different sets for the invalid tracks. What you're showing is just one possibility, and without telling how you got there, it's not necessarily easily verifiable (at least in more complex cases than we've seen so far).

The fact that there are several possibilities to develop an anti-track (or a track) does not change the validity of what I demonstrate. You will see this with the examples I will give on this forum.
The fact that I do not always give the way to develop an anti-track ( or a lead) is undoubtedly embarrassing, I agree and I will try to be more explicit, but do not question the validity of what I do.

Sincerely
Robert

Le fait

[SpAce]

Btw, to be truly rigorous, shouldn't your theorems be accompanied by formal proofs as well? (I'm glad they aren't.)

All my theorems are demonstrated at least in my French document. The theorem 1 TDP part 1 is demonstrated here, I don't understand your criticism!

My criticism was about too much formalism, not too little. If your demonstration is actually a formal proof, so be it (I was looking for a section titled "Proof" as usual). This is an irrelevant point to argue about anyway. All I'm saying is that your presentation doesn't make TDP as easy to digest as I think it could be, at least not for a non-mathematician. But, it's your choice, and I guess you have your reasons to do it that way.

The important qualification being "at this stage". If the construction is continued, things change rapidly.

Explain yourself, because I don't see how the development of P'(E) will challenge what I did?

For example, you could quickly end up with 4r4c7 which would kill 4r4c2. In the Cigarette you could easily end up with 1r3c4 which would kill 15r56c4. However, to get there easily in both cases would require leveraging a contradiction, which makes them poor examples of what I meant. In many situations, like these, there's indeed an obvious set of candidates for either track, but it doesn't mean it's a closed set. If the track is invalid, there's always a different (albeit possibly much more complex) route to construct a conflicting set of candidates.

Here's a simple example of what I mean (from today's puzzle):

Code: Select all

.----------------------.---------------------.-----------------------.
| 159    8       1569  | 3       4     2     | *[1](7)  567  *(1)6   |
| 12     4       126   | 1678    5     1678  |  128     9      3     |
| 7      3       1256  | 1689    89    1689  |  128     2568   4     |
:----------------------+---------------------+-----------------------:
| 1249  *1[7]9   3     | 125789  2789  15789 |  6       247    29    |
| 29     5      *2(7)9 | 4       6     3     | *2[7]89  1      289   |
| 8      6       12479 | 1279    279   179   |  3       247    5     |
:----------------------+---------------------+-----------------------:
| 6      19      1459  | 2589    3     589   |  12489   28     7     |
| 459    2       4579  | 56789   1     56789 |  489     3      689   |
| 3    *[1](7)9  8     | 2679    279   4     |  5       26    *1-269 |
'----------------------'---------------------'-----------------------'

Consider 1r9c9. We can easily construct two mutually incompatible anti-tracks for it, and a third one combining them as well:

Code: Select all

P(1r9c9)        : {1r9c9}

P'a(1r9c9) []   : {1r9c2 7r4c2 7r5c7 1r1c7 1r9c9}
P'b(1r9c9) ()   : {1r1c9 7r1c7 7r5c3 7r8c2 1r9c9}
P'c(1r9c9) []() : {1r9c2 1r1c9 7r4c2 7r1c7 ^7r5c7 ^7r5c3} : contradiction

In this case all of them would prove the same thing: +1r9c9. The point is that there is no "closed set" of candidates that would "necessarily" occur for the anti-track, because it's invalid. In this case there's not even an obvious set because at least the first two possibilities are just as likely. Either way we approach it, it still works because no such closed set is required for proving the desired result.

I just don't agree with your "closed set" idea because it doesn't work globally nor is it necessary.

I believe we will not be able to agree, unless I can convince you one day through examples!

So you don't even count the possibility that I could convince you?

The fact that there are several possibilities to develop an anti-track (or a track) does not change the validity of what I demonstrate.

I haven't said anything about the validity of your results. They're obviously correct. Read again what I've said and actually criticized. The only problem I have is with your definition that seems to imply a single fixed set of (anti-)track candidates. That's misleading, and it's also unnecessary. Since you obviously know the truth, I'm guessing you didn't mean it to be interpreted that way, but in that case the intended interpretation is not obvious at least to me. All I'm saying is that you might want to reconsider the wording of that part, or at least provide a better explanation of what you really mean.

but do not question the validity of what I do.

Oh, I question absolutely everything if it seems necessary Thus far I have not, however, questioned the validity of your logic anywhere, because I haven't seen anything wrong with it. If you think I have, you've misunderstood something. Like I said, I suggest you read again what exactly I have criticized and answer those parts only -- not some imaginary criticism I haven't said or even thought.

[Ajò Dimonios]

Hi Robert e Space,

" Robert Wrote:Property (P1):
If P'(E) is invalid, then at least one candidate Ai of E is a solution in his box.


An anti-track can contain subsets of candidates that form closed sets as defined below.
A set of candidates E1={B1j, j=1.2,...} is a closed set contained in P'(E) when a candidate of each component E1i of E1 is necessarily a candidate belonging to P'(E).

" Space wrote:CODE: SELECT ALL
P(1r9c9) : {1r9c9}

P'a(1r9c9) [] : {1r9c2 7r4c2 7r5c7 1r1c7 1r9c9}
P'b(1r9c9) () : {1r1c9 7r1c7 7r5c3 7r8c2 1r9c9}
P'c(1r9c9) []() : {1r9c2 1r1c9 7r4c2 7r1c7 ^7r5c7 ^7r5c3} : contradiction

In this case all of them would prove the same thing: +1r9c9. The point is that there is no "closed set" of candidates that would "necessarily" occur for the anti-track, because it's invalid. In this case there's not even an obvious set because at least the first two possibilities are just as likely. Either way we approach it, it still works because no such closed set is required for proving the desired result.

In the three tracks of the example of Space, P'a, P'b and P'c, all invalid, there is always a candidate solution, R9C9 = 1 in P'a, r9c9 = 1 in P'b and R1C7 = 7 in P'c. So there is a "closed set" with only one element in each of the three tracks, I deduce that it is therefore in agreement with what was written by Robert.

Ciao a Tutti
Paolo

[Mauriès Robert]

Hi SpAce,

These long exchanges to understand each other on a technical detail certainly show that my poor English obtained by electronic translator does not facilitate the discussion.

Thus, certainly, concerning the definition I give of a closed set contained in an anti-track (or track), the term "necessarily" is not understood in the same way by you and me. For me, I have already written to you it means thatin the construction process chosen this set appears as a closed set. Maybe I need to add that to my definition?

So I agree with you, depending on the construction process chosen, a set may or may not be considered as a closed set of the anti-track (or track).
Your example shows this perfectly. What I'm saying with my definition is that:
- If I choose for P'(1r9c9) the development {1r9c2, 7r8c3,...} then P'(1r9c9) contains 29r5c13, but does not contain 19r47c2.
- If I choose for P'(1r9c9) the development {1r1c9, 7r1c7, 7r5c3,...} then P'(1r9c9) does not contain 29r5c13, but contains 19r47c2.
And there like you, I think it is useless, especially since we immediately see that P'(1r9c9) is invalid which is enough to place the 1r9c9.

It is therefore not this type of situation that I am aiming for with this definition, but the one where we are not able to show the invalidity of the anti-track (or the track) during its construction.
I give you an example on the same puzzle to better explain myself:

P'(6r2c3) = {8r2c7, 8r5c9, 8r7c8, ...} and no visible contradiction!
But the deletion of 6r2c3 makes the closed sets 12r2c13 and 67r2c46 appear.
For me they are closed sets contained in P'(6r2c3) necessarily. However, this anti-track is invalid as evidenced by the complete resolution of the puzzle.

I will end this answer by telling you that if I try to convince you, I do not rule out the opposite, rest assured.

Sincerely
Robert