Hello Eleven.
I think my poor English complicates our communication, I'm sorry.
eleven wrote:I neither understand your theorem nor, what it is for. For this solution you don't need it at all. If you leave out the track steps, it is straightforward guessing.
The example I have chosen to explain this theorem is not good, I agree. So I will give you another example at the end of this message.
eleven wrote:If you allow guessing, someone can point to a backdoor candidate of a very hard puzzle, and tell you, that it solves quite simple. It leads to a solution, and if the puzzle is unique, it is the only possible.
Of course there can be more or less educated guesses, but this is a grey, undefined zone (there were long discussions about them).
If a solution technique uses such guesses, this should be noted at the very beginning (like uniqueness requirement is always noted for uniqueness techniques), because it is a basic difference to all the others.
Be sure, that with such a statement the technique is of no interest anymore for many solvers, and they would be very disappointed, if it turns out after spending much time to understand it.
Are you saying that the TDP, through what you have seen, seems to you to use the riddle ?
Without waiting for your answer, I would like to tell you that in a puzzle every result found by an advanced technique (except perhaps the MSLS) can be found by the TDP. It's the opposite of the riddle, I think.
Concerning the problem of the uniqueness of the solution found, I will talk about it later on, hoping to provide you with answers.
Here is the example I announced earlier.
G = ..82.......6....3.21..56.8.9..84....7..6.9..8....75..2...58..97.4....8.......16..
After reducing the puzzle with the basic techniques (TB), I choose the pair 3r3 to build two conjugated tracks.
Tracks P(3r3c3) and P(3r3c4) are conjugated because P'(3r3c34) is obviously invalid.
P(3r3c3) ={3r3c3, 8r6c2, 5r9c2, 8r9c1,...}.
P(3r3c4) ={3r3c4, 1r6c4,...} contains the set 3r6c123.
As a result we can eliminate 3r45c3 which sees 3r3c3 and 3r6c123.
This is equivalent to a Finned X-Wing on all 3.
We can also eliminate 3r9c1 because P(3r9c1) is invalid in block b7. This is equivalent to an ALS-XZ.
This is to show you that we can do with TIP, the same as with advanced techniques.
But the subject is theorem 4.
The tracks P(3r3c3) and P(3r3c4) are blocked in development. To unlock I will consider another pair, the one in box r7c6, 4r7c6 and the set 23r7c6. As you say elsewhere, necessarily P(4r7c6) or P(23r7c6) is valid and the other is invalid, because these two tracks are conjugated. So I'm going to build them.
P(4r7c6)={4r7c8,...}
P(23r7c6)=P(2r7r6)∩P(3r7r6), so I build separately P(2r7r6) and P(3r7r6).
To make it easier to explain, I mark all these tracks with colors on the puzzle.
P(3r3c3) in yellow, P(3r3c4) in blue, P(2r7r6) in green and P(3r7r6) in purple.
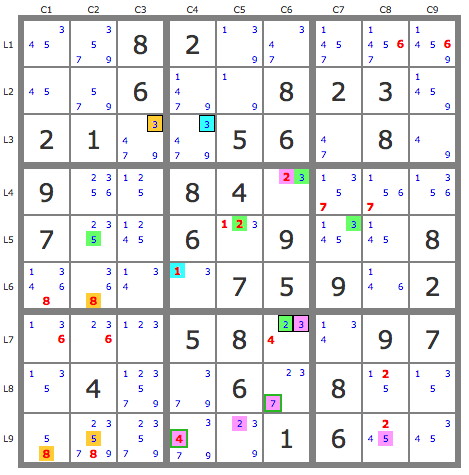
As can be seen, the two tracks P(2r7r6) green and P(3r7r6) purple are opposed to the yellow track P(3r3c3) by the 5. so according to theorem 4 TDP part 3, the candidates of the blue track P(3r3c4) are candidates of the green and purple tracks, therefore are candidates of track P(23r7c6).
Thanks to this I can develop P(23r7c6) which leads to a contradiction ( I'll let you check it out ).
Finally, 23r7c6 can be eliminated, 4r7c6 is the solution and the blue track can be expanded as shown in the following figure.
Several eliminations are then possible (candidate crossed out in red) and two candidates 8 are solutions.
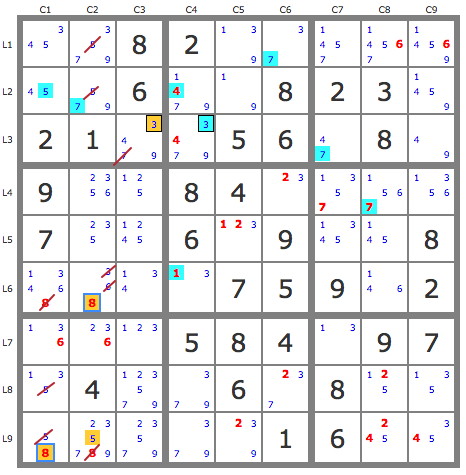
Of course, I can continue until I completely solve the puzzle, but I'd rather wait for your reaction !
Sincerely
Robert



