The New Sudoku Players' Forum

[Mauriès Robert]

Hi Denis,
The difficulties I have in understanding the theories of your book PBCS are linked to my very bad English on the one hand, but also to the mass of concepts and definitions that need to be assimilated. Probably also to my limits in abstract mathematics.
In order to advance in the understanding of the whips that I am particularly interested in sudoku, I would like you to tell me if the following interpretation of the definition of a whip is correct.

A whip is a chain of candidates (Ao, A1, ... An) attached to a target Z linked to Ao, which is constructed by considering as elements of the chain the candidates Ai linked to each other and compatible with Z. A candidate is compatible with Z as long as it does not see Z and does not see a candidate that sees Z.

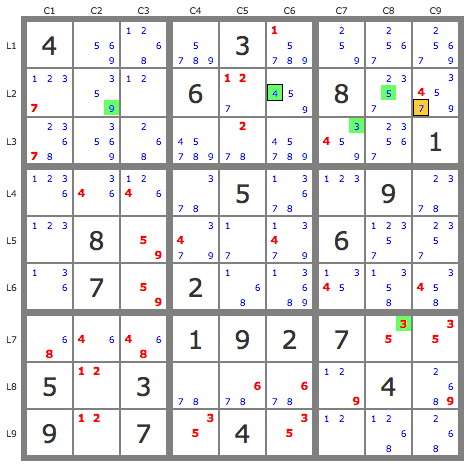
If I take the example of this puzzle detailed in your Subsets in SudoRules
4...3.......6..8..........1....5..9..8....6...7.2........1.27..5.3....4.9........
At the next whip stage
whip [6]: r2n4{c9 c6} - r2n9{c6 c2} - r2n5{c2 c8} - r7c8{n5 n3} - b3n3{r3c8 r3c7} - r3n4{c7 .} ==> r2c9 ≠ 7
My interpretation is as follows:
-4r2c9->4r2c6->-9r2c6->9r2c2(9r2c9 not compatible)->-5r2c2->5r2c8(5r2c9 not compatible)->-5r7c8->3r7c8->-3r3c8->3r3c7->-4r3c7 contradiction => r2c9 ≠ 7 (see puzzle1)

puzzle1: Show

This interpretation of a whip, correct or not, led me to establish (extremely easy demonstration) an interesting result in the practice of the TDP methods that I give you here.

Ao, A1, ... An being candidates who see a Z target,
If the cascade of anti-tracks P'(Ao).P'(A1).P'(A2). . . .P'(An) results in a contradiction, or contains a candidate B who sees Z, then Z may be eliminated.

In the above example, Ao=4r2c9, A1=9r2c9 and A2=5r2c9 and the described string is written P'(Ao).P'(A1).P'(A2) (see puzzle1)

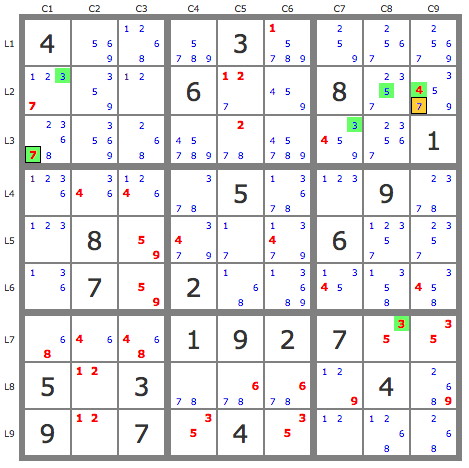
On the same puzzle, we can eliminate 7r2c9 with the cascade P'(7r2c1).P'(7r2c5).P'(7r2c8) which contains 4r2c9 (see puzzle2)

puzzle2: Show

Sincerely
Robert

[denis_berthier]

A whip is a chain of candidates (Ao, A1, ... An) attached to a target Z linked to Ao, which is constructed by considering as elements of the chain the candidates Ai linked to each other and compatible with Z. A candidate is compatible with Z as long as it does not see Z and does not see a candidate that sees Z.

No. Not the definition of compatible, not the definition of a whip.

For Sudoku, the general definition of a whip of length n based on target Z is:
- a sequence of 2n-1 candidates: L1, R1, L2, R2,..., Ln (no Rn),
- a sequence of n CSP-Variables (i.e. of rc-, rn-, cn- or bn- 2D-cells): csp1, ..., cspn
such that
- each Li and Ri is a candidate for the same cspi (i.e. belongs to the same 2D-cell)
- L1 is linked to Z
- each candidate in the sequence is linked to the previous one (continuity property)
- for each 1 ≤ i <n, Ri is the only candidate for CSP-Variable cspi that is not linked to Z or to some previous Rk (k<i) (this is the compatibility of Ri with Z and the previous Rk's)
- all the candidates for cspn are linked to Z or to some Ai (none is compatible with them).

The presence of a whip allows to eliminate the target Z (the proof is obvious).

Such a whip elimination is written
csp1{L1 R1] - csp2{L2 R2} - .... - cspn{Ln .} => not Z
where each cspi looks like r3c4 or r2n3 or c6n8 or b7n4

[Mauriès Robert]

Hi Denis,
So a whip is a defined pattern attached to a target, which if highlighted eliminates the target.
Thus, in practice, we start from a target and try to build the sequences constituting a whip. If we succeed we eliminate the target, if we don't succeed we choose another target, etc.?
Robert

[denis_berthier]

Hi Robert,

So a whip is a defined pattern attached to a target, which if highlighted eliminates the target.

Yes. I don't know what exactly you mean by "highlighted", but if a whip pattern is found on a grid, in exactly the same way a Subset pattern may be found, then the target can be eliminated.

Thus, in practice, we start from a target and try to build the sequences constituting a whip. If we succeed we eliminate the target, if we don't succeed we choose another target, etc.?

It's slightly more elaborate than this. You start by looking for whips[1] in the same way as you look for row/block and column/block interactions (they are the same thing). Then you look for whips[2] and after each elimination, you check if it allows simpler ones (Singles, whips[1]) that were not available before. Obviously, that needs to be done only for patterns in relation with the last elimination.
In the process of looking for whips of some length, you may find longer ones. It's up to you to decide to apply them or not, instead of finishing the systematic search for short ones.
What I mean is, the simplest-first strategy in SudoRules is perfect when one is looking for the solution with the simplest patterns. In practice, a player will take whatever comes.
But the basic idea is not, as you suggest, to start from an arbitrary candidate and try to build the longest possible whip based on it.

[Mauriès Robert]

Hi Denis,
I understand your explanations and I thank you for them.
If the search for whip[1] is extremely easy, these are the alignments that every sudokist knows, if the search for whip[2] is still quite easy, as the basic fish are, as soon as we go to more important lengths, beyond 5.6, ..., whip[n] are not at all easy to find.
It seems to me as random to find these patterns as it is to examine the possibilities of overlapping two conjugated tracks like a track and its anti-track. Experience counts for a lot in both cases.
Cordially
Robert

[denis_berthier]

Hi Denis,
If the search for whip[1] is extremely easy, these are the alignments that every sudokist knows, if the search for whip[2] is still quite easy, as the basic fish are, as soon as we go to more important lengths, beyond 5.6, ..., whip[n] are not at all easy to find.

As for any pattern, long ones are harder to find than short ones.
As reported in chapter 6 of PBCS, 99% of all the puzzles can be solved by whips of length ≤ 5. This is for the real distribution of puzzles. If you consider puzzles generated by the usual top-down or bottom-up generators, the proportion will be much higher.

[Mauriès Robert]

Hi Denis,
The following questions concern the level of difficulty of a puzzle.

1) It seems to me that the note W is one measure of the difficulty of a puzzle, and the note B is another. If this is true, it worries me a bit for two reasons:
- The level of difficulty of a puzzle as it is then defined is not intrinsic, because it depends on the rules we use.
- With the note W, a puzzle requiring at least one whip [6] is more difficult than a puzzle requiring no more whips [3], even though in the first case, the number of operations (the number of times you apply the whips) is less than in the second case. So the difficulty would not be related to the number of operations.

2) With TDP, I have defined a level of puzzle difficulty based on the following two definitions:
- the size of a solution using TDP is equal to the number of contradictions necessary to build the solution and confirm its uniqueness.
- The TDP level of a puzzle is the smallest possible size among all possible resolutions. It is therefore the lower bound of all resolution sizes.
This definition is therefore based more on the number of operations (number of branches of a resolution tree) than on the length of the branches (tracks or anti-tracks).
What do you think about this?

sincerely
Robert

[denis_berthier]

It seems to me that the note W is one measure of the difficulty of a puzzle, and the note B is another. If this is true, it worries me a bit for two reasons:
- The level of difficulty of a puzzle as it is then defined is not intrinsic, because it depends on the rules we use.

There is no absolute rating of a puzzle independent of the set of rules.
There are a priori different W, B, gW, gB, S+W, S+B,... ratings. Each of them is defined intrinsically, is invariant under the all the Sudoku isomorphisms (they are the only known ratings having such properties) and most of them are equal in most cases (see PBCS) .
Being based on theories with the resolution property, the B, gB, S+B and S+gB ratings are obtained at the end of a single resolution path. For whips, what we get after one path is only an approximation of the W rating, but W is generally equal to B; and gW is generally equal to gB. The magic of whips is, they are much simpler than braids, but they are an excellent approximation in most cases. I have spent many pages in PBCS analysing all these relations.

With the note W, a puzzle requiring at least one whip [6] is more difficult than a puzzle requiring no more whips [3], even though in the first case, the number of operations (the number of times you apply the whips) is less than in the second case. So the difficulty would not be related to the number of operations.

This kind of question was already asked by the Sudoku Neanderthals, but nobody had ever been able to define a rating other than the hardest step.
A whip[6] is much harder to find than 3 whips[3], which are still much harder than 9 whips[1].

2) With TDP, I have defined a level of puzzle difficulty based on the following two definitions:
- the size of a solution using TDP is equal to the number of contradictions necessary to build the solution and confirm its uniqueness.
- The TDP level of a puzzle is the smallest possible size among all possible resolutions. It is therefore the lower bound of all resolution sizes.
This definition is therefore based more on the number of operations (number of branches of a resolution tree) than on the length of the branches (tracks or anti-tracks).
What do you think about this?

Your definition depends on what pattern you choose to allow in your tracks. It is no more intrinsic than mine.
It is totally intractable as there are millions of possible resolution trees.

[Mauriès Robert]

Hi Denis
You write

Your definition depends on what pattern you choose to allow in your tracks. It is no more intrinsic than mine.
It is totally intractable as there are millions of possible resolution trees.

I am not claiming that this rating is intrinsic, I am only presenting it to you to get your opinion on a rating of this type, which has nothing to do with yours.
I find your conclusion ("totally intractable") a bit excessive. Indeed, whatever the puzzle, it is always possible to build a resolution tree leading to the solution and its uniqueness, a solution whose size is an upper limit of the level of difficulty. If we cannot be sure of the level of difficulty, at least we can have its maximum value, which can be reduced by testing trees composed from pairs of candidates (or pairs of sets). A solver built on this principle with the objective of reducing this upper bound does not pose any difficulty in my opinion.
Sincerely
Robert
NB: for example, the puzzles proposed by Tarek on this forum, are almost all level 1 TDP and from time to time level 2 TDP.
It would be nice, by the way, that you give from time to time for these puzzles, your resolution with the whips, it would make us (me anyway) better understand this theory. As I also invite you to do it on my site (in French) which is not sectarian to make my readers discover whips.

[denis_berthier]

It is totally intractable as there are millions of possible resolution trees.

I am not claiming that this rating is intrinsic, I am only presenting it to you to get your opinion on a rating of this type, which has nothing to do with yours.
I find your conclusion ("totally intractable") a bit excessive. Indeed, whatever the puzzle, it is always possible to build a resolution tree leading to the solution and its uniqueness, a solution whose size is an upper limit of the level of difficulty. If we cannot be sure of the level of difficulty, at least we can have its maximum value, which can be reduced by testing trees composed from pairs of candidates (or pairs of sets). A solver built on this principle with the objective of reducing this upper bound does not pose any difficulty in my opinion.

There are two problems:
- the basis of your rating (the number of contradictions)
- the absence of any way to compute the minimum or to know how far it is.

for example, the puzzles proposed by Tarek on this forum, are almost all level 1 TDP and from time to time level 2 TDP.

I don't know what you call level 1 TDP, but I guess it's not very different from T&E.

It would be nice, by the way, that you give from time to time for these puzzles, your resolution with the whips, it would make us (me anyway) better understand this theory.

SudoRules has solved millions of puzzles, including some from all the participants of this forum, including Tarek, one of the main puzzle creators.
If you're interested in any specific puzzles, just make a list.

As I also invite you to do it on my site (in French) which is not sectarian to make my readers discover whips.

Thanks, but I'm not sure I'd have time for participating in one more forum. The best place to discover whips is PBCS.

[Mauriès Robert]

Hi Denis,
Thank you for those answers.
PBCS is indeed the reference, but for me and certainly many sudokists it has some drawbacks.
- it is in English, it's not really an obstacle for everyone.
- It's only accessible to people who are sufficiently trained in mathematical logic, there are less people there.
- you have to integrate a lot of definitions, conscepts and properties to have a good understanding of the theory. At the practical level (especially by hand) this does not commit to use the proposed tools.
In short, while I understand the need for mathematical rigor that is yours, in terms of popularization PBCS is not what most people are looking for.
I confess that I still have difficulty understanding all the subtleties of the whips and that I am still stuck on the braids.
I think that a simpler presentation of these techniques for ordinary users would be welcome, because despite the difficulties I still encounter, I find these tools very interesting.
Cordially
Robert

[Mauriès Robert]

Hi Denis,
You wrote

Code: Select all

SudoRules has solved millions of puzzles, including some from all the participants of this forum, including Tarek, one of the main puzzle creators.
If you're interested in any specific puzzles, just make a list.

Would you agree to give me the resolution with whips of Robert's puzzle published on this forum (http://forum.enjoysudoku.com/post288291.html#p288291) and its W-rating.

.1..9.52....2.5...5.23.6..1....8......1...4..4..6.1..5..9...6....67.28...2.9.8.7.

Thank you in advance.
Robert

[denis_berthier]

Would you agree to give me the resolution with whips of Robert's puzzle published on this forum (http://forum.enjoysudoku.com/post288291.html#p288291) and its W-rating.
.1..9.52....2.5...5.23.6..1....8......1...4..4..6.1..5..9...6....67.28...2.9.8.7.

You're welcome

Code: Select all

CLIPS> (solve ".1..9.52....2.5...5.23.6..1....8......1...4..4..6.1..5..9...6....67.28...2.9.8.7.")
***********************************************************************************************
***  SudoRules 20.1.s based on CSP-Rules 2.1.s, config = W+S+Fin
***  using CLIPS 6.31-r761
***********************************************************************************************
.1..9.52....2.5...5.23.6..1....8......1...4..4..6.1..5..9...6....67.28...2.9.8.7.
28 givens, 196 candidates
naked-single ==> r5c4 = 5
naked-single ==> r4c4 = 4
naked-single ==> r1c4 = 8
naked-single ==> r7c4 = 1
hidden-single-in-a-row ==> r9c5 = 6
hidden-single-in-a-row ==> r9c3 = 5
hidden-single-in-a-block ==> r4c2 = 5
hidden-single-in-a-row ==> r9c9 = 4
hidden-single-in-a-row ==> r7c9 = 2
hidden-single-in-a-row ==> r2c5 = 1
Starting_init_links_with_<Fact-3664>
157 candidates, 863 csp-links and 863 links. Density = 7.04719908541565%
whip[1]: c3n4{r2 .} ==> r3c2 ≠ 4, r2c2 ≠ 4
naked-pairs-in-a-column: c1{r8 r9}{n1 n3} ==> r7c1 ≠ 3, r5c1 ≠ 3, r4c1 ≠ 3, r2c1 ≠ 3, r1c1 ≠ 3
whip[1]: c1n3{r9 .} ==> r7c2 ≠ 3, r8c2 ≠ 3
naked-single ==> r8c2 = 4
finned-x-wing-in-rows: n8{r3 r6}{c8 c2} ==> r5c2 ≠ 8
finned-x-wing-in-columns: n8{c9 c3}{r2 r5} ==> r5c1 ≠ 8
whip[1]: r5n8{c9 .} ==> r6c8 ≠ 8
finned-x-wing-in-columns: n6{c2 c8}{r2 r5} ==> r5c9 ≠ 6
biv-chain[3]: r3c7{n9 n7} - r3c5{n7 n4} - b3n4{r3c8 r2c8} ==> r2c8 ≠ 9
biv-chain[3]: r7n7{c2 c1} - r1c1{n7 n6} - c2n6{r2 r5} ==> r5c2 ≠ 7
whip[4]: r3c7{n7 n9} - r2c7{n9 n3} - r1n3{c9 c3} - r4c3{n3 .} ==> r4c7 ≠ 7
whip[4]: r1n3{c9 c3} - r4n3{c3 c6} - r7c6{n3 n4} - r1n4{c6 .} ==> r5c9 ≠ 3
biv-chain[5]: r3c7{n9 n7} - b2n7{r3c5 r1c6} - r1n4{c6 c3} - r1n3{c3 c9} - r8c9{n3 n9} ==> r2c9 ≠ 9
whip[5]: r3c7{n9 n7} - r2c7{n7 n3} - r1c9{n3 n6} - r1c1{n6 n7} - b2n7{r1c6 .} ==> r3c8 ≠ 9
whip[1]: b3n9{r3c7 .} ==> r4c7 ≠ 9, r6c7 ≠ 9
whip[6]: c6n9{r5 r4} - c8n9{r4 r8} - r6c8{n9 n3} - r4n3{c7 c3} - r1n3{c3 c9} - r8c9{n3 .} ==> r5c9 ≠ 9
whip[6]: r8c9{n9 n3} - r1n3{c9 c3} - r4c3{n3 n7} - r4c6{n7 n3} - r7c6{n3 n4} - r1n4{c6 .} ==> r4c9 ≠ 9
hidden-single-in-a-column ==> r8c9 = 9
whip[5]: r2n4{c3 c8} - b3n3{r2c8 r1c9} - b3n6{r1c9 r2c9} - r4c9{n6 n7} - r4c3{n7 .} ==> r2c3 ≠ 3
biv-chain[4]: b1n3{r2c2 r1c3} - b1n4{r1c3 r2c3} - c8n4{r2 r3} - r3n8{c8 c2} ==> r2c2 ≠ 8
biv-chain[5]: b1n3{r2c2 r1c3} - r1n4{c3 c6} - r3n4{c5 c8} - r3n8{c8 c2} - r7c2{n8 n7} ==> r2c2 ≠ 7
whip[5]: r7c2{n7 n8} - c1n8{r7 r2} - r3n8{c2 c8} - c8n4{r3 r2} - r2c3{n4 .} ==> r3c2 ≠ 7
whip[6]: r4c3{n3 n7} - r1c3{n7 n4} - r1n3{c3 c9} - r4c9{n3 n6} - b3n6{r1c9 r2c8} - r2n4{c8 .} ==> r6c3 ≠ 3
biv-chain[3]: c3n3{r4 r1} - r1n4{c3 c6} - r7c6{n4 n3} ==> r4c6 ≠ 3
whip[5]: r4c3{n3 n7} - r6c3{n7 n8} - r6c2{n8 n9} - r6c8{n9 n3} - r4n3{c9 .} ==> r5c2 ≠ 3
whip[6]: r4c6{n9 n7} - b2n7{r1c6 r3c5} - r3c7{n7 n9} - c2n9{r3 r2} - c2n3{r2 r6} - r4c3{n3 .} ==> r4c1 ≠ 9
biv-chain[4]: r3n7{c5 c7} - c7n9{r3 r2} - c1n9{r2 r5} - r5n2{c1 c5} ==> r5c5 ≠ 7
biv-chain[4]: r3c2{n8 n9} - r3c7{n9 n7} - c5n7{r3 r6} - c2n7{r6 r7} ==> r7c2 ≠ 8
naked-single ==> r7c2 = 7
naked-single ==> r7c1 = 8
biv-chain[3]: b1n8{r2c3 r3c2} - r3c8{n8 n4} - r2n4{c8 c3} ==> r2c3 ≠ 7
biv-chain[4]: c5n7{r3 r6} - r6c3{n7 n8} - b1n8{r2c3 r3c2} - r3n9{c2 c7} ==> r3c7 ≠ 7
stte
GRID 0 SOLVED. rating-type = W+S+Fin, MOST COMPLEX RULE TRIED = W[6]
713894526
964215387
582376941
657489213
291537468
438621795
879143652
146752839
325968174

As you can see, W=6

[Mauriès Robert]

Thanks Denis, with this I will be able to better analyze the puzzle and try to understand why I have not managed to reduce the length of my anti-tracks to less than 8 as you can see here or there .
Sincerely
Robert

[Pupp]

Wouldn't be better to use techniques that have been standardidized?

I mean, I'd think the average player would be more comfortable learning techniques that programs such as Sudoku Explainer use.

Truthfully, I haven't had much luck finding information on some of the advanced techniques mentioned by Sudoku Explainer.

I'm still a beginner. I was elated when I got to the "hard" level on Sudoku 10000, but it turns out it doesn't use much in the way of even intermediate level techniques. I'm just about to start the "very hard" levels though.