Overall, Sue De Coq as a subject of discussion seems to appear and disappear periodically, but, more often than not, it doesn’t seem to be on almost anyone’s regular solving radar. Likely, one of the reasons is that it is a fairly complex pattern and unless you have spent a certain amount of time learning to recognize it, it can be easily missed. However, in more than one way, it is a potentially powerful and useful method and is worth the effort to learn.
A few of the important discussions and/or presentations on Sue De Coq:
The original presentation and description of Sue De Coq (Two-Sector Disjoint Subsets) by rubylips:
http://forum.enjoysudoku.com/viewtopic.php?t=2033
Unfortunately, the following thread has been destroyed by hacker activity, but I'll leave the reference here in memory of it.
[This is an interesting thread ‘Sue De Coq revisited’ started by Ruud. Unfortunately, much of its value is lost since a change in the UK forum software creamed the excellent graphics. It’s still worth reading for some of the original thoughts of Ruud and Myth Jellies on the subject: http://www.sudoku.org.uk/SudokuThread.asp?fid=4&sid=8198&p1=5&p2=11]
The Sudopedia description:
http://www.sudopedia.org/wiki/Sue_de_Coq
One of the interesting revelations in the article by Ruud mentioned above is that, according to a limited study he did, the Sue De Coq pattern may not be nearly as rare as people believe. I know that now that I can recognize it more easily, consistent with Ruud’s findings I’m finding it more frequently than some other patterns (eg. jellyfish, hidden triples, naked quads etc.). For that reason and the fact that it can result in several eliminations, it is worth learning, but there is another good reason that I’ll get to in the other thread.
There are several ways of interpreting and finding a Sue De Coq. My preference is to start by seeing its core as either an AALS or AAALS in a row or column within a box. That is, I will first look for the core in the form of either 4 different digit values (aals) or 5 (aaals) in 2 cells in a row or column, all in the same box or in the form of 5 (aals) or 6 (aaals) different digit values in 3 cells in a row or column all in the same box. Next, there should be, in the same box, a bivalue cell (let’s call it A) containing 2 digits that are also present in the core. Then, in the same row or column (as the case may be) there should be a bivalue cell (let’s call it B) containing 2 other digits from the core (ie. not the same digits as were in the bivalue cell A). In addition to the above, if the Sue De Coq is the aaals-type (ie. 5 digit values in 2 cells or 6 in 3 cells) there must also be one more cell in the row or column (let’s call it C) that contains one more digit equal to a digit value in the core, but not present in the other 2 bivalue cells A and B. Usually, in addition to that digit, cell C can only contain digits that are already present in cell B.
A valid Sue De Coq allows the elimination of any digits in the box (outside of cell A) that are equal to those in cell A. Likewise, all digits in the row or column (outside of cell B and C of course) equal to those in cell B and those in cell C can be removed. Also, if there is one digit value left in the core, not present in A, B or C, all digits equal to that value in the box or in the row or line can be eliminated.
Those newer to solving may find the principle behind the Sue De Coq difficult to understand. Here’s my take: Ultimately, the core will need to have 2 digits (if a core of 2 cells) or 3 digits (if a core of 3 cells) to ‘survive’. If you think about it, cells A and B (the bivalue cells in the box and in the row or column) are sucking away 2 of the possible digit values that the core needs to ‘survive’. Those digits must be either in cells A, B or in the core; that accounts for the basic eliminations in the box and in the row or column. Likewise, if the core is an aaals (ie. 5 digit values in 2 cells or 6 digit values in 3 cells), cell C will potentially suck away a 3rd digit value and accounts for the associated eliminations in the row or column. Finally, this usually leaves one digit value left in the core which must be there for the core to ‘survive’ and it accounts for the associated eliminations of that digit in the box and the row or column.
All of this should be made clearer by the examples below.
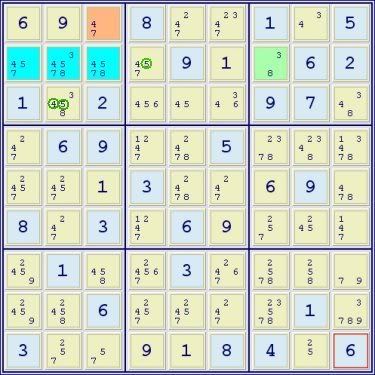
This is the simpler aals-type Sue De Coq (5 digit values in the 3 blue cells). The brown cell is the A cell; the green cell is the B cell as described above. The 4 can be eliminated from r3c2 because of the 4 in cell A. The 5 in r3c2 and in r2c4 can be removed because of the digit value 5 in the core not present in either cell A or B. There are no digits available for elimination (ie. equal to 3 or 8) in row 2.
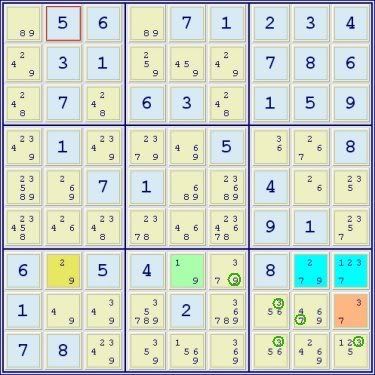
This is the slightly more complex aaals-type Sue De Coq (5 digit values in the two blue cells). The 3s and the 7 can be removed from box 9 due to the digit values in the brown cell A. The 9 can be eliminated from r6c6 due to the 9 in the green cell B. The gold cell C accounts for the 3rd digit, 2, in the aaals of the core, but there are no 2s in the row to eliminate.
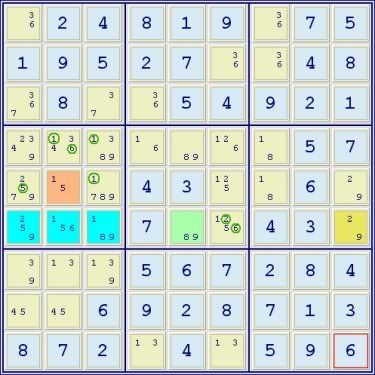
This is another aaals-type Sue De Coq which not only represents all of the possible components of a Sue De Coq, but also is an example of the many eliminations that are possible. The 1s and 5 in box 4 are eliminated due to the 1 and 5 in the brown cell A. There are no eliminations possible in row 6 due to the green cell B. 2 can be eliminated due to the 2 in the gold cell C. The 6s in box 4 and row 6 can be eliminated because of the 6 that is not represented in cells A, B, or C and is thus locked to the core.
Again, this description of Sue De Coq is meant primarily as an introduction to the subject of The Almost Sue De Coq. As such, it covers the more common, but not all of the possible forms of the pattern. In summary, the benefit of learning to find and use Sue De Coq can be looked at this way: It can be found more frequently than a number of patterns that manual solvers are used to looking for, but it can often also provide many more eliminations than those patterns. In addition, the Almost Sue De Coq, as described in the follow-up thread, can be one more useful addition to the toolbag for advanced manual solving.
(Puzzle credits: 1st is my own, 2nd from the Player’s forum Zoo, 3rd from Ruud’s ‘Sue De Coq revisited’ thread. ASI stands for Advanced Solving Illustrated.)

