The New Sudoku Players' Forum

by **David P Bird** » Wed May 30, 2012 9:41 pm

champagne I now understand your distinctions, and so it seems does ronk. As the analysis you then need to perform to convert a partial Exocet to an Exocet is outside my experience I'll stay quiet on that subject.

You wrote:That thread is titled "exotic patterns a resume" and I opened it to exchange on all tools that can be used in hardest puzzles. I hope it will stay true and I would not see it limited to the Jexocet.

Yes I can appreciate that. I consider it your thread and won't do anything to spoil your aim for it.

All I would ask is that when you cover the topic of what to do once an Exocet (and presumably a JExocet) is found, you distinguish between the two of them when the methods diverge. If that is done then it probably wouldn't be necessary to split the thead into two.

by **champagne** » Thu May 31, 2012 6:04 am

ronk wrote:Below is (I think) a "partial exocet" for puzzle #12177, simpler than the one on your web page. Note the targets are r4c2=1236 and r7c1=1236 just as if it were a "full exocet." This can only happen because there is an indication for the other target. Evidently this cause has yet to be formulated in the definition, so I'll try to do so.
___

interesting view it seems we have to interleaved partial exocet (unchecked for r12c7 as target)
clearly a logic to investigate

BTW I am not sure I published the list of puzzles having a similar potential

by **daj95376** » Fri Jun 01, 2012 5:24 pm

FWIW: For puzzle "12177", three of the four values in r12c3 work as a JExocet:

Code: Select all: 98.7.....7...6......5..97..5....84...9.6...3...4.2...1.5....8.....3....6....1..2. ;10.80;10.80;10.50;GP;kz0;12177;23 +--------------------------------------------------------------------------------+ | 9 8 1236 | 7 345 12345 | 12356 1456 2345 | | 7 1234 123 | 12458 6 12345 | 12359 14589 234589 | | 12346 12346 5 | 1248 348 9 | 7 1468 2348 | |--------------------------+--------------------------+--------------------------| | 5 12367 12367 | 19 379 8 | 4 679 279 | | 128 9 1278 | 6 457 1457 | 25 3 2578 | | 368 367 4 | 59 2 357 | 569 56789 1 | |--------------------------+--------------------------+--------------------------| | 12346 5 123679 | 249 479 2467 | 8 1479 3479 | | 1248 1247 12789 | 3 45789 2457 | 159 14579 6 | | 3468 3467 36789 | 4589 1 4567 | 359 2 34579 | +--------------------------------------------------------------------------------+ # 173 eliminations remain r12c3=1 => r4c2=1 and/or r7c1=1 r12c3=3 => r4c2=3 and/or r7c1=3 r1 c3=6 => r4c2=6

That leaves r12c3=2, which doesn't comply with my understanding of a JExocet. However, of the 13 combinations of <1236> that are acceptable for this grid, only 5 combinations contain r12c3=2, and each of these contain values from the base set in r4c2 and r7c1.

Hidden Text: Show

I'm assuming that the relationship on <2> is represented somewhere in the results posted by others.

by **ronk** » Fri Jun 01, 2012 8:20 pm

daj95376 wrote:I'm assuming that the relationship on <2> is represented somewhere in the results posted by others.

Not yet. I've been trying to find something simple, but so far, nothing as simple as expected. For #12177:

r12c3=1 implies strong inference (1)r4c2 = (1)r7c1
r12c3=3 implies (3)r4c2 = (3)r7c1
r1c3=6 implies r4c2=6 as a hidden single

Combine any two of a, b, and c, and there is effectively a remote hidden pair.

But there's still the <2>. If r12c3=12, based on Xsudo's result there is apparently the strong inference (126)r4c2 = (126)r7c1. But we already know of the existence of (1)r4c2 = (1)r7c1, implying (26)r4c2 = (26)r7c1. To be clear, this means if both candidates are missing from r4c2, one of them must exist in r7c1. I say "apparently" because I don't see it in the strong inferences of the Xsudo graphic, only as inferred from the candidates remaining in the target cells.

The result is similar for r12c3=23, i.e., (236)r4c2 = (236)r7c1.

The result for r12c3=26 is r4c2=6 and r7c1=26, allowing for the possibility of both target cells holding <6>.

champagne wrote:BTW I am not sure I published the list of puzzles having a similar potential

I don't believe you have yet. A few more might help clarify the rules for "partial exocets."

by **daj95376** » Sat Jun 02, 2012 5:49 am

What bothers me about puzzle #12177 is that, even though three of the values in r12c3 act like an Exocet with respect to cells r4c2 and r7c1, the final solution does not.

Code: Select all: +-----------------------+ | 9 8 6 | 7 . 1 | 2 . 3 | | 7 . 2 | . 6 3 | 1 . . | | 3 1 5 | 2 . 9 | 7 6 . | |-------+-------+-------| | 5 6 . | 1 3 8 | 4 . 2 | r4c2=6 | 2 9 1 | 6 . . | . 3 . | | . 3 4 | . 2 . | 6 . 1 | |-------+-------+-------| | 6 5 3 | . . 2 | 8 1 . | r7c1=6 | 1 2 . | 3 . . | . . 6 | | . . . | . 1 6 | 3 2 . | +-----------------------+ # in solution

Would someone please remind me of the final objective???

by **champagne** » Sat Jun 02, 2012 6:38 am

daj95376 wrote:What bothers me about puzzle #12177 is that, even though three of the values in r12c3 act like an Exocet with respect to cells r4c2 and r7c1, the final solution does not.

Would someone please remind me of the final objective???

that thread is dedicated to any "exotic pattern" that can help to solve potential hardest puzzles.

puzzle 12177 is a puzzle with a very high solving potential in floors 1236.
The final objective here is to find (if any )an easy logic similar to the already known that can lead to eliminations;

It appears that that puzzle is a partial "exocet pattern" and I developed a full solution based on that property.
Ronk has the finger on something different, but not yet clear in it's last post.

it's quite clear that the solution in that case is not one of the pair complying with the exocet digit per digit rules, so the result in the target is unpredictable.

by **champagne** » Sat Jun 02, 2012 6:43 am

here is a list of puzzles (including puzzle 12177) having a high solving potential using only 4 or 5 digits.
Unless I made an error in the selection process, there should be no exocet, no sk loop, no rank 0 multifish in it.

The last data in each line is the smallest digits group showing a good potential.
For some of these puzzles, a 5 digits group showed a much higher potential, but it seems reasonable to focus on the smallest group.

Hidden Text: Show

by **David P Bird** » Sat Jun 02, 2012 11:29 am

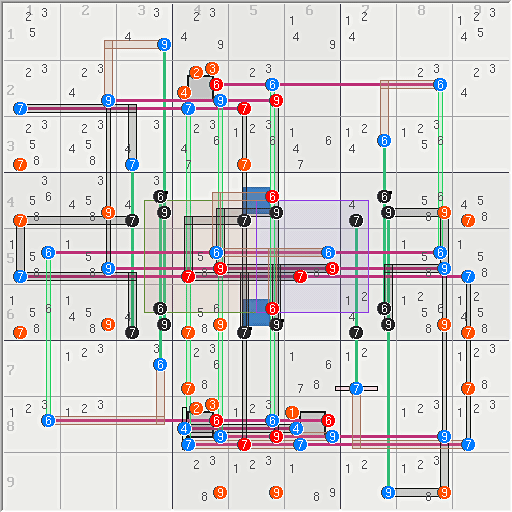
98.7..6..5.7.4..3...2......4...3..1..7......8..6...2.....3.4.9.....95.......7...1;r9c4 r9c6 r7c1 r8c8 268 Lot3:414

Code: Select all: *-------------------------*-------------------------*-------------------------* | 9 8 134 | 7 125 13-2 | 6 245 45-2 | | 5 16 7 | 12689 4 12689 | 189 3 29 | | 136 1346 2 | 1569-8 1568 1369-8 | 14579-8 4578 4579 | *-------------------------*-------------------------*-------------------------* | 4 259 589 | 25689 3 26789 | 579 1 5679 | | 123 7 1359 | 14569-2 1256 169-2 | 3459 456 8 | | 138 1359 6 | 1459-8 158 179-8 | 2 457 34579 | *-------------------------*-------------------------*-------------------------* | 278-16 1256 158 | 3 16-28 4 | 578 9 2567 | | 278-136 1346-2 134-8 | 16-28 9 5 | 3478 28-467 23467 | | 36-28 34569-2 3459-8 | 28-6 7 28-6 | 345-8 456-28 1 | *-------------------------*-------------------------*-------------------------*

(268)TwinJExocet:r9c46,r8c8,(7)r78c1 => r7c1 <> 1, r8c1 <> 13, r8c8 <> 47

Compatibility check:
(2)r8c8 = (2)r1c8 - (2)r2c8 = (2#2)r29c46
(6)r8c8 = (6)r5c8 - (6)r9c1 = (6#2)r59c46 (incompatible)
(8)r8c8 = (8)r3c8 - (8)r2c7 = (8#2)r29c46
. . => r78c1,r9c46,r8c8 <> 6, (base & target cells)
. . r9c18 <> 28, r9c2 <>2, r9c7 <> 8, r7c5,r8c4 <> 28, (seen by base cells)
. . r8c2 <> 2, r8c3 <> 8, (seen by targets (278)r78c1 & (28)r8c8 )
. . r1c68 <> 2, r3c467 <> 8, (fin cells to "skewed" Swordfish)
. . r5c46 <> 2, r6c46 <> 8 (seen by the alternative X-wings (2)r9+[2|5]c46 & (8)r9+[2|4]c46)
(32 eliminations to this point from the nearly resolved pattern)

The key step now is to analyse the URs that can be made with the twin digit (7)r78c1 in the JExocet band
The threats are (27)r78c19 and (78)r78c16

(7)r6c8 = (7-8)r3c8 = (8-2)r8c8 =[JE]= (2#2)r78c19 -[UR]- (7#2)r78c19 = (7#2)r78c17 => r4c7 <> 7

This step, which is dependent on the derived JExocet inference, opens up the puzzle to being solvable by AICs. I suspect it may be a common feature of Twin JExocets, and without it I would have to resort to it nets.

by **champagne** » Sat Jun 02, 2012 2:56 pm

David P Bird wrote:98.7..6..5.7.4..3...2......4...3..1..7......8..6...2.....3.4.9.....95.......7...1;r9c4 r9c6 r7c1 r8c8 268 Lot3:414

That one is clearly in Platinum Blonde's family.

It is number 414, does it mean that others are not

by **daj95376** » Sat Jun 02, 2012 4:55 pm

David's latest puzzle for consideration. A modest observation.

Code: Select all: 98.7..6..5.7.4..3...2......4...3..1..7......8..6...2.....3.4.9.....95.......7...1 ;r9c4 r9c6 r7c1 r8c8 268 Lot3:414 +--------------------------------------------------------------------------------+ | 9 8 134 | 7 125 123 | 6 245 245 | | 5 16 7 | 12689 4 12689 | 189 3 29 | | 136 1346 2 | 15689 1568 13689 | 145789 4578 4579 | |--------------------------+--------------------------+--------------------------| | 4 259 589 | 25689 3 26789 | 579 1 5679 | | 123 7 1359 | 124569 1256 1269 | 3459 456 8 | | 138 1359 6 | 14589 158 1789 | 2 457 34579 | |--------------------------+--------------------------+--------------------------| | 12678 1256 158 | 3 1268 4 | 578 9 2567 | | 123678 12346 1348 | 1268 9 5 | 3478 24678 23467 | | 2368 234569 34589 | 268 7 268 | 3458 24568 1 | +--------------------------------------------------------------------------------+ # 173 eliminations remain r9c46=26 and r8c8<>2|6 => r78c1=26 r9c46=28 and r8c8<>2|8 => r78c1=28 r9c46=68 and r8c8<>6|8 => r78c1=68 r8c8=4 => r78c1<>7 => X-Wing r78\c79 => r36c8=7 => r8c8<>4 r8c8=7 => r78c1<>7 => ~7[r7] => r8c8<>7

by **champagne** » Sat Jun 02, 2012 5:23 pm

daj95376 wrote:David's latest puzzle for consideration. A modest observation.

r9c46=26 and r8c8<>2|6 => r78c1=26
r9c46=28 and r8c8<>2|8 => r78c1=28
r9c46=68 and r8c8<>6|8 => r78c1=68

r8c8=4 => r78c1<>7 => X-Wing r78\c79 => r36c8=7 => r8c8<>4
r8c8=7 => r78c1<>7 => ~7[r7] => r8c8<>7
[/code]

No objection to any elimination based on the specificity of the puzzle.

What is interesting in David's path is that

- the puzzle is recognised as a twin exocet
- the abi loop works for 26 68 (invalid) leaving only 28 as valid

So in once, he comes to 32 eliminations.

The puzzle in not yet solved, but it is severely downgraded.

by **ronk** » Sat Jun 02, 2012 6:14 pm

champagne wrote:
David P Bird wrote:98.7..6..5.7.4..3...2......4...3..1..7......8..6...2.....3.4.9.....95.......7...1;r9c4 r9c6 r7c1 r8c8 268 Lot3:414
That one is clearly in Platinum Blonde's family.

Yes it is, and back in Jan 2009 Allan Barker posted a Truth/Link Solution ("TLS", aka "logic set", aka "SLG") using the then unnamed exocet with an "undecided target cell" (r8c46) and four AURs in this morph of Platinum Blonde, for 36 exclusions. For details, see link. Truths 679R5 are not actually required, however, for exactly the same exclusions.

by **daj95376** » Sun Jun 03, 2012 10:46 am

Since we have a twin JExocet, I guess it's time to look for a quad JExocet.

Code: Select all: Puzzle #3323 in "02 index.txt": 98.7..6....5.6.......9.4...4..3..9..37...8.....6.9......2.1.3.........52........1 +------------------------------------------------------------------------------------------+ | 9 8 134 | 7 235 1235 | 6 1234 345 | | 127 1234 5 | 128 6 123 | 12478 Q4789-123 Q4789-3 | SL on <9> | 1267 1236 137 | 9 2358 4 | 12578 12378 3578 | |-----------------------------+-----------------------------+------------------------------| | 4 125 18 | 3 257 12567 | 9 12678 5678 | | 3 7 9 | 12456 245 8 | 1245 1246 456 | | 1258 125 6 | 1245 9 1257 | 124578 R3478-12 R3478-5 | SL on <3> |-----------------------------+-----------------------------+------------------------------| | 5678 4569 2 | 4568 1 5679 | 3 46789 46789 | | 1678 13469 13478 | 468 3478 3679 | B478 5 2 | | 5678 34569 3478 | 24568 234578 235679 | B478 46789 1 | +------------------------------------------------------------------------------------------+ # 183 eliminations remain ### -478- quad JExocet Base = r89c7 Target = (9)r2c89,(3)r6c89

by **champagne** » Sun Jun 03, 2012 11:26 am

daj95376 wrote:Since we have a twin JExocet, I guess it's time to look for a quad JExocet.

Code: Select all
Puzzle #3323 in "02 index.txt": 98.7..6....5.6.......9.4...4..3..9..37...8.....6.9......2.1.3.........52........1 +------------------------------------------------------------------------------------------+ | 9 8 134 | 7 235 1235 | 6 1234 345 | | 127 1234 5 | 128 6 123 | 12478 Q4789-123 Q4789-3 | SL on <9> | 1267 1236 137 | 9 2358 4 | 12578 12378 3578 | |-----------------------------+-----------------------------+------------------------------| | 4 125 18 | 3 257 12567 | 9 12678 5678 | | 3 7 9 | 12456 245 8 | 1245 1246 456 | | 1258 125 6 | 1245 9 1257 | 124578 R3478-12 R3478-5 | SL on <3> |-----------------------------+-----------------------------+------------------------------| | 5678 4569 2 | 4568 1 5679 | 3 46789 46789 | | 1678 13469 13478 | 468 3478 3679 | B478 5 2 | | 5678 34569 3478 | 24568 234578 235679 | B478 46789 1 | +------------------------------------------------------------------------------------------+ # 183 eliminations remain ### -478- quad JExocet Base = r89c7 Target = (9)r2c89,(3)r6c89

Fine and a quick look tells me it should be 47 in the base (abi loop works)

by **David P Bird** » Sun Jun 03, 2012 12:41 pm

champagne wrote:Fine and a quick look tells me it should be 47 in the base (abi loop works)

After which my quick look says a (1256)Shark or Multi-fish, followed by a step to avoid a (37)UR:r36c89 should do it.

The New Sudoku Players' Forum

Exotic patterns a resume

Re: Exotic patterns a resume

Re: Exotic patterns a resume

Re: Exotic patterns a resume

Re: Exotic patterns a resume

Re: Exotic patterns a resume

Re: Exotic patterns a resume

Re: Exotic patterns a resume

Twin JExocet Continuation

Re: Twin JExocet Continuation

Re: Exotic patterns a resume

Re: Exotic patterns a resume

Re: Twin JExocet Continuation

Re: Exotic patterns a resume

Re: Exotic patterns a resume

Re: Exotic patterns a resume