PIsaacson wrote:The following is a 5 petal Death Blossom from the royle17 collection:
[............]
The ALS chain r8c4.<n58> -8- r8c8.<n28> -2- r8c6.<n12> -1- r14569c5.<n145678> => r7c5 is the closest match to the DB, but my engine doesn't find any equivalent for r5c4 or something that covers both in one fell swoop.
Some of the Death Blossoms posted here are true beauties that might be described in a variety of ways however, PIsaacson's Royal 5 is really something different. (For the sake of argument, I have included one of the two eliminations but the second one follows the same argument)
- Code: Select all
Puzzle #9 royle17 36628 collection [from PIsaacson]
+------------------+------------------------+----------------------+
| 38 5689 35679 | 345678 45678 34567 | 3689 1 2 |
| 4 2568 1356 | 3568 9 12 | 368 3678 3678 |
| 12 689 3679 | 3678 12 367 | 3689 5 4 |
+------------------+------------------------+----------------------+
| 138 7 3459 | 2 (456) 34569 | 13568 3689 35689 |
| 6 2589 1359 | 379-5 (57) 3579 | 4 23789 135789 |
| 23 459 3459 | 1 (4567) 8 | 2356 3679 35679 |
+------------------+------------------------+----------------------+
| 7 1 8 | 4569 2456 4569 | 2356 3469 3569 |
| 9 46 46 | (58) 3 (12) | 7 (28) 158 |
| 5 3 2 | 46789 (14678) 4679 | 168 4689 689 |
+------------------+------------------------+----------------------+
DEB2 20 Nodes, Rank = 2 (linksets - sets)
7 Sets = {8N4 4569N5 8N6 8N8}
9 Links = {28r8 5c4 467c5 5b5 18b8}
1 Elimination --> r5c4<>5
Just a quick summary to help explain.
Rank 0 One class of logic always has N strong sets (truths) that can be contained inside of N links (rank 0). This includes continuous loops, most fish, and hidden/naked multiples. "Links" only means contained in the same house/cell or, "can see".
Rank 1 A second class of logic always has N strong sets that can be contained inside of N+1 links (rank 1), which includes most all chains and most all other Sudoku methods.
But not this baby.
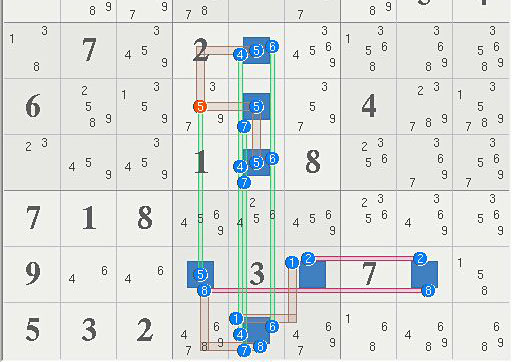
In this case, all seven cells can only be covered using 9 links, which makes this logic rank 2 (rare). Then according to rank rules, any candidate contained in 3 links, or seeing 3 cells, can be eliminated.
But, 5r5c4 sees only 2 cells through box 5b5 and through column 5c4. The answer is that the triplet 5r8c4 decreases the rank along the path containing column link 5c4, then the 2 overlapping links eliminate 5r5c4. (Likewise, another group of cover sets will eliminate candidate 5r7c5 in PIsaacson's example.).
Although interesting, it's not clear to me to see how exactly this relates to the various ALS rules.
.


