The New Sudoku Players' Forum

[Myth Jellies]

Based on Peter's PM

The following is from the solution log for Royle17 #40:

Code: Select all

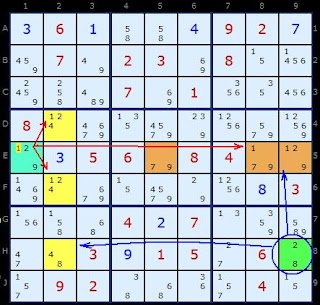
Royle17 #40 after simple eliminations:

 8        B27-9     A29       |4         6         3        |79        1         5       
A46       B457-6     57-6     |9         1         2        |67        8         3       
 3       AB69        1        |7         8         5        |69        4         2       
 --------- --------- ---------+--------- --------- ---------+--------- --------- ---------
 7         8         4        |2         5         6        |3         9         1       
 9        B56        56       |1         3         7        |4         2         8       
 1         23        23       |8         9         4        |5         7         6       
 --------- --------- ---------+--------- --------- ---------+--------- --------- ---------
 5        B79        8        |6         4         1        |2         3         79       
 2         34-9      39       |5         7         8        |1         6         49       
 46        1         67       |3         2         9        |8         5         47       

do_alschains - graph contains 104 vertices and 1388 edges
do_alschains - reducing r2c2.<4567> by <6> dual
do_alschains - reducing r2c3.<567> by <6> dual
do_alschains - reducing r1c2.<279> by <9> dual
do_alschains - reducing r8c2.<349> by <9> dual
do_alschains - sdc+c[2x6/6] b1x348.<2469> +24+ r12357c2.<245679>

Not an SDC, but truly a bizzare dual-linked overlapping, cannibalistic dual-linked ALS. I can't explain the candidate eliminations is terms of subset counting, especially the r1c2 <> 9 and r2c2 <> 6, but these types of ALSs are "all over the place" and all the eliminations are valid. Another example:

Your deduction is just overlapping ALS's where the two restricted common digits (2&4) are not part of the overlap. This is not CoALS, but rather just an ALS loop.

The AIC using ALS's for this deduction would be something like

(4&5&6&7&9=2)r12357c2 - (2=6&9&4)r1c3|r2c1|r3c2 - (4=2&5&6&7&9)r12357c2...AIC-loop

When ALS's are in an AIC loop, any digits in the ALS which do not have a weak link in the loop must be a part of that ALS. Thus the endpoints tell us that 5679 must be in B, and we also know that 6&9 must be in A. We can see this more easily if we cut the AIC-loop so that the endpoints are part of ALS 'A'.

(2&6&9=4)A - (4=5&6&7&9&2)B - (2=4&6&9)A...AIC-loop

Here it is easy to see the reason for the so-called cannibalistic deduction.

As Ron pointed out, there is also a hidden or AHS version of the deduction which might be easier to find. Noting that the 3's are locked in r68c2 while 5&7 are locked in r12c2|r2c3, we also have

(2&3)r2c68 = (2&5&7-5&7&4)r12c2|r2c3 = (4&3)r2c68...AIC-Loop

This loop implies that any digits not shown cannot exist in r1268c2|r2c3

CoALS would tell you that either 6&9 must exist in the combined A&B cells, or that 2&4&5&7 must exist in those same cells. If there was some cell or set if cells which prevented one of those premises from being true then you would know that the other premise was true. Generally this is just a quick check for certain examples of subset counting. As an slightly better example that could lead to a deduction, if we had

Code: Select all


 8         27       A29       |4         6         3        |79        1         5       
A46        457-6     57-6     |9         1         2        |67        8         3       
 3       AB69        1        |7         8         5        |69        4         2       
 --------- --------- ---------+--------- --------- ---------+--------- --------- ---------
 7         8         4        |2         5         6        |3         9         1       
 9         56        56       |1         3         7        |4         2         8       
 1         23        23       |8         9         4        |5         7         6       
 --------- --------- ---------+--------- --------- ---------+--------- --------- ---------
 5        B79        8        |6         4         1        |2         3         79       
 2         34        39       |5         7         8        |1         6         49       
 46        1         67       |3         2         9        |8         5         47       

We could form the intersecting A & B ALS's as shown. Then either 6&9 or 2&4&7 (or both) are true in cells marked with A and/or B. Since r1c2 contains only 27 and it sees all the 2's and 7's in A+B we know that it must be true that A+B contains 6&9 and we could elminate the 6 in r2c2. Usually there will be a simpler way than CoALS to make a deduction, but every now and then there isn't. Note also that CoALS requires at least 3 elements to make its deduction--the combined intersecting pair of ALS's and the cell or set of cells which eliminates one of the options (or at least weakly links to one of the options).

[edited to add second removal of a candidate in the diagram]

[ttt]

Hi All,
This thread seems... IMO, it's should be on other... (perhaps, solver programs)
BTW, champagne: no new for long time (at least for me... )

ttt

[DonM]

I just find it rather nice to see Myth posting....about anything actually.

[champagne]

Hi All,

BTW, champagne: no new for long time (at least for me... )

ttt

Right ... and reverse.

I took the opportunity of a quiet period here to code in a clean way what has been established clearly on the Exocet side. I have still to analyze PB special situation and the last findings of Ronk and Allan with mini row based SLG of rank 0 leading to a huge number of eliminations.

I have also checked new lots prepared by coloin and ot promissing results.

I have to sort out all the files on some criteria as
easily "solved" by SK loop, Exocet, exocet+SKloop, several exocet...
and still to be investigated (excuding SLG eliminations)..

All this is time consuming, but if you need to be feeded with specific stuff, I can make a quick extraction.

BTW, using full potential power of exocets and subject to a final check, the solver gives now a solution for Golden Nugget 1/5 of the previous runtime and same for the printsize.

This is achived for a big number of puzzles.

One strange result at the end is that the old AI ETANA puzzle goes up in the file of hardest just because I could not find something special for it. It stays now in my final ranking over Eastern Monster.

BTW what are your last findings

champagne

[PIsaacson]

Hi All,
This thread seems... IMO, it's should be on other... (perhaps, solver programs)...
ttt

Upon reflection, I concur. I'll be opening a thread in the solver programs forum.

FYI: For those who have downloaded the ALS engine. I refreshed the source/executable. It now can generate *.sud collections for examination in XSudo and has the option of using the former RCD rules, or the new RCD rules (off by default). AHS integration is still in debugging. Send me PM if you can't figure out the options from the '-help'.

[PIsaacson]

Another refresh, but this time with the added bonus of including Death Blossom. I was intrigued by a posting from Allan Barker which included a DB that "looped" and essentially formed a dual-linked ALS. Death Blossom is an interesting ALS formation, so I decided that I needed to include it in my ALS engine.

I haven't had much time to really experiment with it, but preliminary results show that DBs occur much more frequently than I would have expected. In conjunction with short ALS chains, this is a powerful set of tools. I'm using my engine to extract xsudo *.sud collections of various DBs and studying them to learn how to spot these beasts manually. Using a DonM SDC style approach, I'm starting with an initial stem cell AALS.

So, if you are interested in looking at lots of Death Blossoms, PM me and I'll tell you the secret of how to get them. Or else you could just use the help (what meager help there is), or just try it against something like the royle17 and see what happens.

Cheers,
Paul

[aran]

Further to Death Blossom (DB)
An analysis for consideration :

DB can be analysed in two alternative ways.
1. as a simple hidden set structure
2. as a rank 1 base set/cover set structure

First let's posit the DB requirements :
- ALS A
- ALS B
- outside bivalue (a,b) cell C

* where a sees all instances of a in ALS A
* where b sees all instances of b in ALS B

- z is the elimination candidate in outside cell D which sees all instances of z in ALS A and ALS B.
That's five items...too much like hard work.

Now let's work backwards to profile into a simple hidden set structure :
A={a z x} where x stands for all other candidates in ALS A
B={b z y} where y stands for all other candidates in ALS B
C=(a,b)
D=(z,w) where w stands for all other candidates in cell D

Now look at this from a hidden set perspective : we have
zx=a-a=b-b=zy
ie a chain where the confrontation of first and last nodes (as it happens grouped nodes) zx and zy eliminates any z which they mutually see : ie z in cell D.
I strongly maintain that the hidden set approach is crying out to be exploited wheres the multiple constraints to set up the Death Blossom pattern don't really deserve the effort to locate them.

Lastly as a base/cover set approach, it can be readily seen that DB is a Rank 1 structure ie 1 more cover set than base set.

As was recently noted, the most interesting structures known today have Rank 0 structure (doubly-linked ALS and nice loops). So DB doesn't fall into that category.

In a word, DB strikes me as a dépassé construct, with unnecessarily complicated "set-up" requirements given that there is a simple structure (hidden set) which achieves the same purpose quicker, and further being a Rank 1 structure, its dividends will be limited.

[PIsaacson]

Aran,

The reason I'm interested in DB is exactly because they allow setting up dual-linked ALSs in cases where the "normal" ALS chaining rules don't apply.

Specifically: http://forum.enjoysudoku.com/viewtopic.php?p=67972#p67972

Allan Barker characterized the example as an ALS loop, but another way of looking at it is a DB with a bi-location stem cell. That was what I was alluding to in my first paragraph. I should have included the url reference. Mea culpa...

I haven't finished coding DB, but in loading examples in Xsudo, I have seen examples of rank 0 structures involving the use of such bi-local stems. I even have some really interesting tri-value and tri-local DBs that contain a dual-linked ALS on 2 of the 3 petals.

Preliminary findings on the royle17 collection show that DBs are prevalent, and as compared to ALS chains size 3 (including all possible dual-links), dual and tri value/location stem celled DBs are more powerful.

Using my ALS engine:

Code: Select all

sudoku -bvw -Xprsa -A9 -B1 royle17.txt -- just ALS
     1596 unsolved, 7755 passes for 58300 eliminations
sudoku -bvw -Xprsk -A9 -B1 royle17.txt -- just DB
      387 unsolved, 6355 passes for 76142 eliminations
sudouk -bvw -Xprsak -A9 -B1 royle17.txt -- both ALS and DB
      324 unsolved -- regardless of using -Oprsak or -Oprska to place ALS before/after DB

... there is a simple structure (hidden set) which achieves the same purpose quicker

Could you please explain or give references? In your example, it looks like you are using an AIC to link/extend the RCD(s) of 2 ALSs. If so, then how is this different from ALS grouped nice-loops? I don't understand the hidden set reference. Yet another gaping hole in my understanding of sudoku theory/techniques...

Cheers,
Paul

[DonM]

In my view, the Death Blossom is closely related to ALS Chains. In fact, the 'simplest' form as in the example from Sudopedia, is nothing more than a 3-Set ALS Chain in which the r1c8 'stem cell' is simply a bivalue middle set in the chain whereby, the restricted common 1, links it to the blue r137c5 set and the restricted common 8 links it to the yellow r5c469 set. (The following was in the original ALS Chain tutorial in Eureka, but was removed when the tutorial was revised for this forum: ...above, I noted the similarity of the 3-set ALS Chain to that of the simplest form of Death Blossom ie. the middle ALS being a bivalue cell.) Thus, to understand ALS Chains is to understand the Death Blossom and from that point of view IMO, it's not all that complicated or complex.




The same thing is true of this example used elsewhere:

[PIsaacson]

Don,

I agree that DBs are very closely related to current ALS chains, especially with bi-value stems. However, bi-location stems are not covered by the current ALS chaining rules, unless each bi-local is also a bi-value and even then you need my modified RCD adjacency rules to get XY-chain extensions to work correctly.

It's the tri/quad/quint value/location stem cells that are unique with DBs. These constitute a "network" of interacting ALSs that are absolutely not covered by ALS chains. My ALS engine can be used to demonstrate this very easily. Also, the stem cell can be a "one of anything" mutually exclusive/weakly linked set of candidates. Currently, I only consider multi-value cells and multi-location single value candidates within a sector. I'll be expanding that soon.

Other possibilities exist for both multiple value and single value sets of candidates as stem cells: http://forum.enjoysudoku.com/viewtopic.php?p=35379#p35379

Likewise, I don't think the Death Blossom is any more difficult to understand/find than ALS chains. But then again, I'm really a devotee of all things ALS'ish. Without your tutorial on SDCs, I would never have thought myself capable of finding those manually. Perhaps you might consider something similar for DBs???

Cheers,
Paul

[Luke]

Here's another Death Blossom, but I prefer to see it as two hidden sets with a bivalue in between:

Code: Select all

 *-----------------------------------------------------------*
 | 2     3     1-4   | 6     9     457   | 15   *147   8     |
 | 457   156   9     | 48    578   3     | 156   2     567   |
 | 4578  568   456   | 2     1     45    | 9     34    367   |
 |-------------------+-------------------+-------------------|
 | 9     4     3     | 7     6     2     | 8     5     1     |
 | 6     25    25    | 1     3     8     | 7     9     4     |
 | 1     7     8     | 5     4     9     | 23    6     23    |
 |-------------------+-------------------+-------------------|
 | 358   568   7     | 48    2     145   | 156  *13    9     |
 | 58    9     26    | 3     58    17    | 4    *17    26    |
 | 345  *12   *124   | 9     57    6     |*23    8     257   |
 *-----------------------------------------------------------*


(124)r9c237=(3)r9c7-(3=1)r7c8-(17)r18c8=4(r1c8) =>r1c3<>4.

It's the tri/quad/quint value/location stem cells that are unique with DBs. These constitute a "network" of interacting ALSs that are absolutely not covered by ALS chains.

Could you post an example of this, i.e. a DB that can't be written as a chain?

[DonM]

Here's another Death Blossom, but I prefer to see it as two hidden sets with a bivalue in between:

Code: Select all

 *-----------------------------------------------------------*
 | 2     3     1-4   | 6     9     457   | 15   *147   8     |
 | 457   156   9     | 48    578   3     | 156   2     567   |
 | 4578  568   456   | 2     1     45    | 9     34    367   |
 |-------------------+-------------------+-------------------|
 | 9     4     3     | 7     6     2     | 8     5     1     |
 | 6     25    25    | 1     3     8     | 7     9     4     |
 | 1     7     8     | 5     4     9     | 23    6     23    |
 |-------------------+-------------------+-------------------|
 | 358   568   7     | 48    2     145   | 156  *13    9     |
 | 58    9     26    | 3     58    17    | 4    *17    26    |
 | 345  *12   *124   | 9     57    6     |*23    8     257   |
 *-----------------------------------------------------------*

I see it, once again, as just a 3-set ALS Chain (aka ALS xy-wing rule) with a bivalue middle set at r9c7 whereby the restricted common 3 joins it with one set at r178c8 and restricted common 2 with the other set at r9c23. Thus those two flanking sets both 'see' the 4 at r1c3. Not sure why one would want to re-invent the wheel?

Edit: I find that looking on those structures as hidden sets just complicates things because IMO, they are operating as ALSs as part of an ALS chain. In my mind (and maybe only in my mind), I prefer to see hidden sets as the structure whereby an elimination can be made right away and an almost hidden set as that where an elimination could be made if not for one digit in the same house. That way, I can more easily keep what I view as ALSs separate from AHPs.

[ronk]

Mike Barker is the originator of the Death Blossom term. Would someone please provide a link to where Mike said the "stem" of a Death Blossom could be smaller than a tri-valued cell

[PIsaacson]

The following is a 5 petal Death Blossom from the royle17 collection:

Code: Select all

Puzzle #9 royle17 36628 collection
.......124...9...........5..7.2.....6.....4.....1.8....18..........3.7..5.2......

After elementary constraint processing (minimal SSTS without coloring or XY-wings):

 38        5689      35679    |345678    45678     34567    |3689      1         2
 4         2568      1356     |3568      9         12       |368       3678      3678
 12        689       3679     |3678      12        367      |3689      5         4
 --------- --------- ---------+--------- --------- ---------+--------- --------- ---------
 138       7         3459     |2       BC456       34569    |13568     3689      35689
 6         2589      1359     |379-5  BCD57        3579     |4         23789     135789
 23        459       3459     |1       BC4567      8        |2356      3679      35679
 --------- --------- ---------+--------- --------- ---------+--------- --------- ---------
 7         1         8        |4569      246-5     4569     |2356      3469      3569
 9         46        46      AE58        3        A12       |7        A28        158
 5         3         2        |46789    *14678     4679     |168       4689      689

db[5] stem cell r9c5.<14678> ALS[1]-1-r8c468.<n1258> ALS[2]-4-r456c5.<n4567> ALS[3]-6-r456c5.<n4567> ALS[4]-7-r5c5.<n57> ALS[5]-8-r8c4.<n58> => r5c4<>5, r7c5<>5

ALS A overlaps with ALS E (fully contains it!)
ALSs B and C are identical so this ALS is a dual-linked petal
ALSs B/C and D overlap (fully contained)

The ALS chain r8c4.<n58> -8- r8c8.<n28> -2- r8c6.<n12> -1- r14569c5.<n145678> => r7c5 is the closest match to the DB, but my engine doesn't find any equivalent for r5c4 or something that covers both in one fell swoop.

If you download my engine and run: "sudoku -bv -Xprsk -A9 -K5 puzzle.in" you'll see the incredible number of DBs it can find for one puzzle.
Compare that with "sudoku -bvw -Xprsa -A9 -B2 puzzle.in" or try "-B6" for really long ALS chains.

[DonM]

Mike Barker is the originator of the Death Blossom term. Would someone please provide a link to where Mike said the "stem" of a Death Blossom could be smaller than a tri-valued cell

One could also ask for a link where Mike said it couldn't be smaller than a tri-value cell. Pending clarification from Mike himself, the bi-value cell example seems to have been accepted by no less than Ruud (if memory serves, he put up the Sudopedia example) and Andrew Stuart, who uses the 2nd bi-value example I posted above in his book...