The New Sudoku Players' Forum

[SpAce]

Hi Robert,

Thanks for your TDP example!

1) P(2r5c56)={6r4c4, ...} and P'(2r5c56)={2r6c56, 5r6c8, 5r79c7, 5r2c9, 6r1c9, 9r1c6, 9r5c5, 6r4c4,...} => r4c4=6 + 5 validation and 1 elimination by basic techniques.

Here's how I'd write the equivalent logic as an AIC:

(7=12)r6c56 - r5c56 = (2456-9)r5621c9 = r1c6 - (9=127)b5p689 => +7 r6c6 (=> +6 r4c4, ...)

2) P(1r9c1) and P(2r9c2) are conjugated, because P'({1r9c1,2r9c2})={6r8c5, 3r8c3, 8r9c6,... contradiction} => P'({1r9c1,2r9c2}) invalid.

This part is interesting! You're basically establishing a derived strong link between 1r9c1 and 2r9c2. That's creative! Here's how I'd write that piece of logic:

(1|2=68)r9c12 - (6|8=196)r8c348 - (6)r7c8 = r7c123 - (68=1|2)r9c12 => +(1|2)r9c12

I like that. However, it seems that we have a bit of a terminology clash that I didn't notice before when you talked about conjugated tracks. When we say two things are conjugated it means they have an XOR relationship (like par candidates in GEM), i.e. exactly one must be true. You've only established that at least one must be true (strong link), but not that they both couldn't be (weak link). Thus the relationship is OR, not XOR, and thus not conjugate in our terminology. It's what we would call a strong-only link between the two candidates (at least one must be true, but both could be). The distinction is important. For example, if you could prove that 1r9c1 is true it wouldn't automatically invalidate 2r9c2, like it would if they were truly conjugate.

P(1r9c1)={1r9c1, 46r15c9, 3r7c1, 8r3c1, 8r2c8, ...} and P(2r9c2)={2r9c2, 38r3c12, 8r2c8, ...} => r2c8=8.

So here you're using the derived OR between those two tracks. That works, but I think you're using it a bit inefficiently. My coloring with those two reveals five common singles: +1r9c1 => +3r3c2, +3r7c3, +8r2c8, +8r3c2, and additionally +2r7c2 (because 2r9c2 runs into a contradiction). In fact, it would be enough to show that 2r9c2 -> contradiction, because it would give us both +2r7c2 (naturally) and +1r9c1 (due to the derived strong link). As an AIC:

grid: Show

Code: Select all

.------------------------.-------------------------.-----------------.
|  46      1      246    |  5       8       b29    | 7    3     269  |
|  7       9     d268    |  124     123      123   | 145  1258  1256 |
| d38    d(2)38   5      |  1249    7        6     | 149  1289  129  |
:------------------------+-------------------------+-----------------:
|  2       7      3      |  6       5        4     | 8    19    19   |
|  146     56     146    |  8       129     b129   | 3    7     245  |
|  9       58    c148    |  3      c12       7     | 6    25    245  |
:------------------------+-------------------------+-----------------:
|  136   a[2]36  a1[2]69 |  7       4       b1259  | 159  1569  8    |
|  5       4     e1689   | f19     f1369    f1389  | 2    169   7    |
|  1-68    68-2   7      | f1(2)9  f1(2)69   12589 | 159  4     3    |
'------------------------'-------------------------'-----------------'

[(2)r7c23 = (2,91)r715c6 - (18)r6c53 = (832)b1p678] = (8)r8c3 - (8=13692)b8p45678 => -2 r9c2 => +1 r9c1

That would get us here:

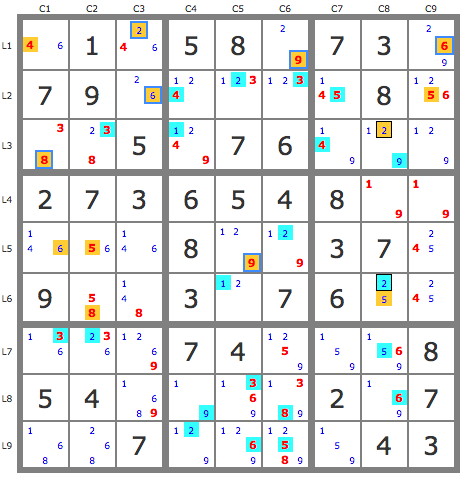
Code: Select all

.-------------.------------------.-----------------.
| 46  1   246 | 5     8     29   | 7    3     269  |
| 7   9   26  | 124   123   123  | 145  8     1256 |
| 8   3   5   | 1249  7     6    | 149  129   129  |
:-------------+------------------+-----------------:
| 2   7   3   | 6     5     4    | 8    19    19   |
| 46  56  146 | 8     129   129  | 3    7     245  |
| 9   58  148 | 3     12    7    | 6    25    245  |
:-------------+------------------+-----------------:
| 3   2   69  | 7     4     159  | 159  1569  8    |
| 5   4   689 | 19    1369  1389 | 2    169   7    |
| 1   68  7   | 29    269   2589 | 59   4     3    |
'-------------'------------------'-----------------'


Hodoku offers a neat final move for that puzzle state:

hodoku final move: Show

Code: Select all

.--------------------.---------------------.------------------.
| 46   1       246   |  5      8      29   | 7     3     269  |
| 7    9      b6'2   |  124   *123    123  | 145   8     1256 |
| 8    3       5     |  1249   7      6    | 149   129   129  |
:--------------------+---------------------+------------------:
| 2    7       3     |  6      5      4    | 8     19    19   |
| 46   56      146   |  8      129    129  | 3     7     245  |
| 9   a5[8]    14-8  |  3     a2'1    7    | 6    a25    245  |
:--------------------+---------------------+------------------:
| 3    26     b69    |  7      4      1259 | 159   1569  8    |
| 5    4     bc69(8) | c91    c691'3  1389 | 2    c691   7    |
| 1    26-8    7     |  29     269    2589 | 59    4     3    |
'--------------------'---------------------'------------------'

Death Blossom:

(1)r2c5 - (1=258)r6c582
||
(2)r2c5 - (2=698)r278c3
||
(3)r2c5 - (3=1698)r8c5843

=> -8 r6c3,r9c2; stte

--
The same as an AIC:

(8)r8c3 = [(962)r872c3 & (6913)r8c3485] - (2|3=1)r2c5 - (1=258)r6c582 => -8 r6c3,r9c2; stte

Back to your solution:

3) Like you, to make it quick, P(1r3c8) invalid, P(2r3c8) solution.

I don't fully understand this last part. As you can see in the grid above, even with my extra placements there are still three candidates in r3c8. What happened to your 9r3c8? If you want to prove +2r3c8 directly like that, I think you should invalidate both 1 and 9 in r3c8 (or otherwise 19r34c8, or more simply 2r6c8). Maybe that's what you meant, but it should be stated more clearly, like: P(19r34c8) invalid (my preference) or P(1|9)r3c8 invalid. Do you agree?

[Mauriès Robert]

Hi SpAce,

I don't fully understand this last part. As you can see in the grid above, even with my extra placements there are still three candidates in r3c8. What happened to your 9r3c8? If you want to prove +2r3c8 directly like that, I think you should invalidate both 1 and 9 in r3c8 (or otherwise 19r34c8, or more simply 2r6c8). Maybe that's what you meant, but it should be stated more clearly, like: P(19r34c8) invalid (my preference) or P(1|9)r3c8 invalid. Do you agree?

Oh, excuse me, I had a typing error. It was not P(1r3c8) that I wanted to write but P(19r3c8).

Donc, P(19r3c8)= {19r34c8, 6r8c8, 5r7c8, etc... contradiction} et P(2r3c8) solution.

We can also see by drawing the two tracks on the puzzle, it is more visual, that several candidates are common to both tracks and by validating them this allows to finish the puzzle with the basic techniques, which quickly appeal to the contradiction.

P(129r3c8)=P(19r3c8)∩P(2r3c8)={9r6c5, 9r1c6, 6r2c3, etc...}

However, it seems that we have a bit of a terminology clash that I didn't notice before when you talked about conjugated tracks. When we say two things are conjugated it means they have an XOR relationship (like par candidates in GEM), i.e. exactly one must be true. You've only established that at least one must be true (strong link), but not that they both couldn't be (weak link). Thus the relationship is OR, not XOR, and thus not conjugate in our terminology. It's what we would call a strong-only link between the two candidates (at least one must be true, but both could be).

No, we give the same meaning to the conjugated term. It is possible with my definition that two conjugated tracks (TDP part 2) are both valid, but it is impossible that both tracks are invalid at the same time.
In this example, tracks P(1r9C1) and P(2r9C2) are conjugated, but I do not need to know which one is valid to conclude that 8r2c8 is placed (theorem 3 TDP part 2).
Moreover, this is perhaps where TDP is an original approach with the notion of anti-tracking and the theorem 1 TDP part 2.

Sincerely
Robert

[SpAce]

Oh, excuse me, I had a typing error. It was not P(1r3c8) that I wanted to write but P(19r3c8).

Ok, that's what I thought.

However, it seems that we have a bit of a terminology clash that I didn't notice before when you talked about conjugated tracks. When we say two things are conjugated it means they have an XOR relationship (like par candidates in GEM), i.e. exactly one must be true. You've only established that at least one must be true (strong link), but not that they both couldn't be (weak link). Thus the relationship is OR, not XOR, and thus not conjugate in our terminology. It's what we would call a strong-only link between the two candidates (at least one must be true, but both could be).

No, we give the same meaning to the conjugated term.

I still don't think so. This is clearly in conflict with our usual definition of "conjugated":

It is possible with my definition that two conjugated tracks are both valid, but it is impossible that both tracks are invalid at the same time.

Like I just said above, that's the definition of a strong-only link -- not a conjugate link which is both strong and weak. Don't you see the difference between "at least one must be true" and "exactly one must be true"? Only the latter is conjugated in our terminology:

Code: Select all

Weak      : NAND  : at most one can be true (i.e. both can't be true but both can be false)
Strong    : OR    : at least one must be true (i.e. both can't be false but both can be true)
Conjugate : XOR   : exactly one must be true (both weak and strong, both NAND and OR)

Your definition which allows both tracks to be valid is simply an OR relationship, not XOR. So, it's not conjugate in our commonly accepted terminology which is defined for example here. Or is there something I misunderstood?

In this example, tracks P(1r9C1) and P(2r9C2) are conjugated,

No, they're not. They're just strongly-linked. As you just said, they could both be true. Thus not conjugate.

but I do not need to know which one is valid to conclude that 8r2c8 is placed

That's true. Normally we just use the strong link property (OR) without needing to worry about whether it's conjugate (XOR) or not. It works here as well. In fact, AICs don't distinguish between normal strong links and conjugate links at all. They're treated the same way: both as OR. Yet that doesn't mean that all strong links are conjugate -- only the XOR links are.

In fact, GEM does make a distinction between the two types. Opposite par-candidates are conjugates, but opposite super-candidates are not (they're just strongly linked). In this case the 1r9c1 and 2r9c2 would be opposite super-candidates instead of par-candidates, even though they're used as seeding candidates for the coloring, because they're NOT conjugates. The same happens when for example guardians of deadly patterns (like URs, BUGs, Oddagons, etc) are used as seeds. We only know that at least one of them must be true (i.e. they have a strong link), but several or all of them could be just as well, so they're not conjugates like native strong links (bivalues, bilocations, etc) where exactly one candidate can (and must) be true.

Moreover, this is perhaps where TDP is an original approach with the notion of anti-tracking and the theorem 1 TDP part 2.

Or perhaps not. I can't make definite judgments because you've made your explanations so complex, but no matter how many times I try to read them, I can't see anything that is not explainable by simple AIC links. I could be wrong, but this is how I see your terms and their relationships to ours:

Code: Select all

Track vs Anti-Track : conjugate (exactly one valid)
"Conjugated Tracks" : strongly linked (at least one valid)
Opposite Tracks     : weakly linked (at most one valid)

If that's correct, then your anti-tracks are in fact conjugates (to their corresponding tracks), while your "conjugated tracks" are not (necessarily).

Another interesting part in your documentation:

Definition:
An anti-track P'(E) is said to contain a set of candidates E1={B1j, j=1,2,...} when a candidate of each component E1i of E1 is necessarily a candidate belonging to P'(E).

What do you mean by "necessarily"? If the starting condition is invalid then there's no such concept, as any candidate can be forced to become part of the resulting set. Only valid tracks have definite members. Invalid tracks can have anything. So, unless you know beforehand that your P'(E) track is valid, you can't have a definite list of candidates that belong to it.

[Mauriès Robert]

Hi SpAce,

I will not respond step by step to your comments, but I will give a global answer.

I now better understand with your explanations the difference between the different types of relationships between candidates (or groups of candidates) that you consider: weak, strong and conjugated.

In TDP, I never talk about links, I only talk about tracks and like you I give definitions: tracks, anti-tracks, opposite tracks, conjugated tracks. As you know, a definition is not something to be discussed, it is a state set by the person who makes the definition. Only you love or you don't love.
I chose the conjugated word (without knowing what you mean by it) in reference to my knowledge of mathematics (complex number theory). No doubt that at the time, if I had been aware of your definition, I would have used another word to avoid confusion. That's the way it is!

So we are not talking about the same things. But if we want to try comparisons, I would say that XOR links compare to conjugated tracks that are also opposite, but only if the puzzle is a single solution.

You say that TDP is complex, that's not my opinion. Perhaps the theoretical presentation I have made here seems complex because of its rigorous nature, but in its application it is simple because there is little to know: 4 definitions (track, anti-track, conjugated track, extensions) and 4 theorems. With some examples we quickly understand how to use TDP.

Of course, everything that can be done with TDP can also be done with other techniques, everyone chooses what they prefer.

You will see from the examples I will provide that TDP is easy to apply, provided, of course, that its definitions are used.

One last thing, finally. I think it would be more useful for those interested in our TDP exchanges if these exchanges were made on the TDP feed.

I also thank you for the time you spend understanding me and TDP.

Sincerely
Robert

[International_DBA]

Hello, I have been busy with my Facebook group so haven't been back for a while.
The last thing I remember was a Dr Moist Hands (I think that was his/her name) introducing me to Hodoku.
He/she explained how to run the Hodoku jar file in batch mode.
I have been using it for a while now.
First I choose a solution I like then with a simple shell script I run my program 100 times to produce 100 different puzzles all with the same solution.
If I want a really tough one I use grep on all the Hodoku analysis to pick out the Extreme ones then choose the one(s) with the highest values for further evaluation.
Here is one I created a couple of days ago.
I would be interested to know what you think about it:
https://andrewspuzzles.blogspot.com/202 ... treme.html

[Leren]

Code: Select all

*-----------*
|3..|5..|624|
|2..|.6.|.3.|
|...|...|..5|
|---+---+---|
|9..|.5.|2..|
|.1.|..7|...|
|.3.|.4.|.6.|
|---+---+---|
|...|...|8.2|
|..6|7..|1..|
|1..|.98|...|
*-----------*
3..5..6242...6..3.........59...5.2...1...7....3..4..6.......8.2..67..1..1...98...