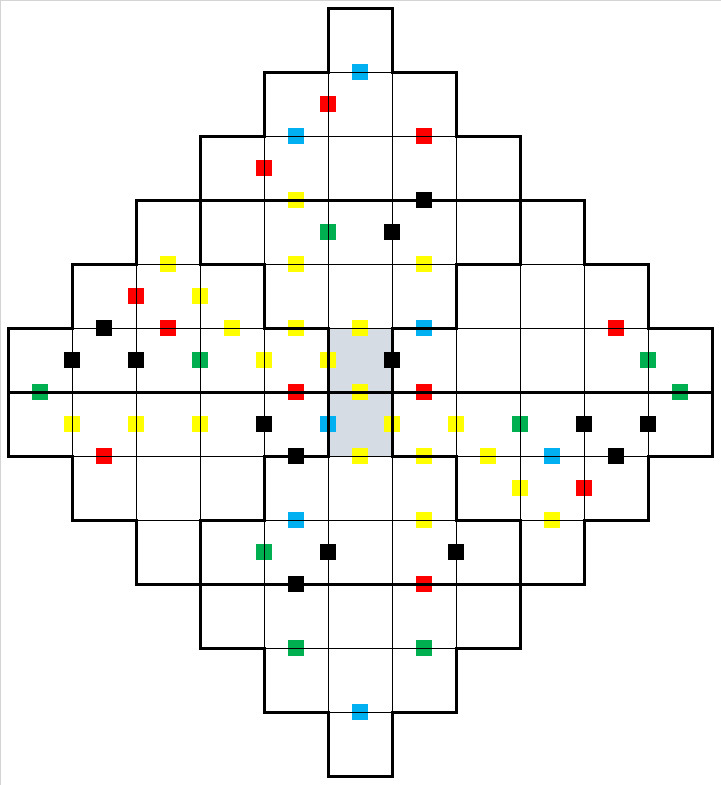
I have not created a Triankle for a while. This one is Semi-Symmetric and the clues are Meandoku
Meandoku the following colour clues apply:
Green: the sum of the two adjacent cells is 8 or 9 only
Blue: the sum of the two adjacent cells is ten
Red: the sum of the two adjacent cells is 11 or 12 only
Yellow: the sum of the two cells is below eight
Black: the sum of the two cells is above twelve
Triankle Rules
The numbers are from 0 to 9.
There are 8 triangular nonets covering twelve rows and 11 columns.
The two different numbers in the centre two grey cells repeat horizontally and vertically. I.e. in row six there are eleven numbers so nine different numbers with the grey number twice and row seven the same. In column 6 there are 12 numbers eight different numbers with the two grey numbers twice.
The other eight numbers do not repeat anywhere.
The repeating numbers are present in every nonet.
Each of the other eight numbers is absent in one and only one nonet.
So Semi-symmetric Rules.
There are five pairs of numbers which are unknown.
If a cell contains a number the opposite cell must contain it or its partner.
At least on cell pair will be asymmetric and at least one cell pair will be symmetric. Ideally in total the ratio will be around 50%:50%
Note this implies that if a number is missing from a nonet its partner is missing from the opposite nonet.
Quite hard, my solution path swung backwards and forwards between using meandoku clues and semi-symmetry.
If you wish to solve in JSudoku:
open as a 12 by 12 Latin Square from 0 - B
enter the eight nonets as killer cages with no sum (c, then choose operator "none")
select a cell in C6: ctrl right click select remove and then C6
select a cell in R6: ctrl right click select remove and then R6
select a cell in R7: ctrl right click select remove and then R6 (JS has renumbered the rows)
select all the nonet cells shift A then shift B to remove the A & B pencilmarks
do a set of solves to put A B in every cell around the diamond.
select r67c6 as a twin killer cage with no sum (twin killer is easier to see)
select r6 c1-5 & c7-11 as a twin killer cage 45/10
select r7 c1-5 & c7-11 as a twin killer cage 45/10
select r1-5&r8-12 c6 as a twin killer cage 45/10
Save as your TRIANKLE BASE
Or use the attached zip

