The example graphics pretty much tell the story so not much further explanation is necessary except to point out that if one extra digit, beyond that necessary for a valid Sue De Coq, is present in either the core 2 or 3 cells (ie. the aals or aaals within the same box), the bivalue cell A in the box, the bivalue cell B in the row or column or the additional cell C (if present) then that digit can be used as the basis for the strong link.
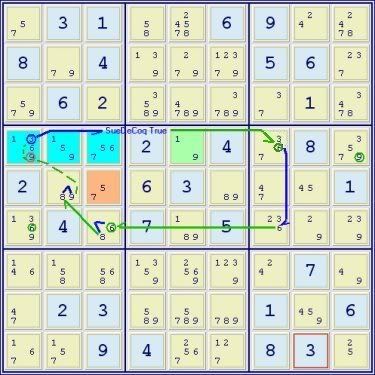
But for the 3 in r4c1, the basic Sue De Coq pattern is present: the core blue cells (an aals with 1,5,6,7,9 in 3 cells), the brown cell A with 5,7 and the green cell C with 1,9. The logic is straightforward: If not 3 in r4c1 then the Sue De Coq is true and any of the circled green cells are valid weak link ‘targets’. In this case a relatively simple chain eliminates the 9 in r4c1:
aic:
(3)r4c1 = suedecoq[(15679)r4c123/r4c5(19)/r5c3(57)] - (6)r4c7 = r6c7-(6=8)r6c3 - (8=9)r4c2 => r4c1<>9
nice loop:
r4c1 -9- r4c1 =3= suedecoq[(15679)r4c123/r4c5(19)/r5c3(57)] -6- r4c7 =6= r6c7 -6- r6c3 -8- r5c2 -9- r4c1 => r4c1<>9
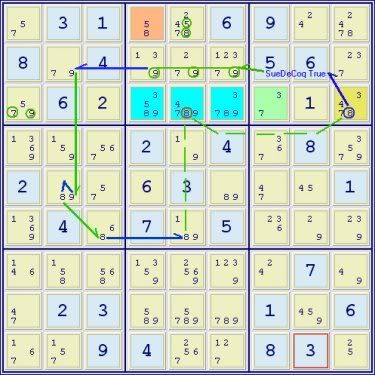
Here, the situation appears a little more complex, but the principle is the same. Once again, but for one digit, the 8 in r3c9, there would be a valid Sue De Coq. In this case, the core is an aaals (3,4,5,7,8,9 in 3 cells), the brown cell A contains 5,8, the blue cell B contains 3,7 and there is a gold cell C present containing the extra digit 4 necessary because of the aaals of the core. However, cell C also contains one extra digit 8 that makes the Sue De Coq invalid. The logic is similar to the previous example: If not 8 in r3c9 then the Sue De Coq is true and any of the circled green cells are valid weak link ‘targets’. This example shows that not only are there several of the latter available, but also that occasionally a group may be available. The chain above takes advantage of the group of 9s in r3c456.
aic:
(8)r3c9 = sdc[(345789)r3c456/r1c4(58)/r3c7(37)/r3c9(347)] – grp(9)r2c456 – r2c2 – (9=8)r4c2 – r6c3 = (8)r6c5
nice loop:
r3c5 -8- r3c9 =8= sdc[(345789)r3c456/r1c4(58)/r3c7(37)/r3c9(347)] -9- r2c456 =9= r2c2 -9- r5c2 -8- r6c3 =8= r6c5 -8- r3c5
The question might be raised as to whether most or all chains using an almost-sdc could be subsumed by other chains. However, given all the possibilities using the almost-sdc, I rather doubt it. There is, in fact, a separate chain that can be used to achieve the same elimination in the first example above. There may be one also for the second example; I didn’t look very hard. Even if it were possible to find alternate chains for most or all of the possible almost-sdc chains (again, which I doubt), finding an almost-sdc pattern allows one to see many more possibilities at once rather than having to search them out individually. Also is the fact that, in a given overall solution, a chain using an almost-sdc pattern may be possible without requiring a previous move that might have been necessary for an alternate route to achieve the same elimination making the overall solution shorter (more elegant?). Not to mention that the Sue De Coq is a ‘what is’ pattern. There is no additional assumptivity compared to other basic ‘almost’ patterns that makes it less attractive for use.
Finally, I mentioned that the almost Sue De Coq pattern should be found even more frequently than Sue De Coq itself. If you haven’t noticed already, note that the two examples above are not only from the same puzzle, but are at exactly the same point in the puzzle!
(The above puzzle is the UK forum Weekly Extreme #109 ER=8.4. ASI stands for Advanced Sudoku Illustrated)

