The New Sudoku Players' Forum

[denis_berthier]

DonM,

Very good, but where's the better example?

[Luke]

You're saying SdC "may" be more frequent than it seems. If you want to raise interest in it, it's your job to prove this or at least to give a more convincing example.

Don has now posted Ruud's frequency list in the other thread (ASI#1.) Given Ruud's credibility it carries some weight.

I think the whole idea here has been that Joe the Pencil Solver might benefit from an awareness of SdC, and that Almost SdC is the next step. It's helped me out.

I love my computer, but when I do a puzzle I sharpen a pencil.

[denis_berthier]

I love my computer, but when I do a puzzle I sharpen a pencil.

I wasn't critcising SdC but only DonM's understated claims on frequency - and I don't yet take them for granted, even after Ruud's list (see my answer in the other thread). Frequency depends on the order in which the rules are considered; but Ruud provided no information on this.
Is there an example that can't be solved by AICs with ALSs?

[DonM]

I love my computer, but when I do a puzzle I sharpen a pencil.

I wasn't critcising SdC but only DonM's understated claims on frequency - and I don't yet take them for granted, even after Ruud's list (see my answer in the other thread).

That might be said to be a form of oxymoron. If someone is understating a point or in, other words, qualifying a point, then the premise that you are being asked to take the point for granted is one of your own making. This is supposed to be an interesting & enlightening discussion on SDC & aSDC, patterns that can be both useful and fun to find in manual solving. The fun premise needs no investigation; one would have to be a numbnuts to not get a rise out of finding an SDC in a puzzle.

However, the overall relative usefulness remains to be seen. But IMO to raise an idea that is being floated to some sort of academic level where proof is demanded and lists requested before the next class (figuratively) misses the whole point of this hobby. If that's what floats your boat, then why not come up with a study that totally disproves any premise I'm raising? Otherwise, lighten up and enjoy the discussion. For instance, you might have at least said something like, 'Gee, Ruud's list is interesting, I didn't know someone had even made a list like that.'.

[ronk]

But for the 3 in r4c1, the basic Sue De Coq pattern is present: the core blue cells (an aals with 1,5,6,7,9 in 3 cells), the brown cell A with 5,7 and the green cell C with 1,9. The logic is straightforward: If not 3 in r4c1 then the Sue De Coq is true and any of the circled green cells are valid weak link ‘targets’. In this case a relatively simple chain eliminates the 9 in r4c1:

aic:
(3)r4c1 = suedecoq[(15679)r4c123/r4c5(19)/r5c3(57)] - (6)r4c7 = r6c7-(6=8)r6c3 - (8=9)r4c2 => r4c1<>9
nice loop:
r4c1 -9- r4c1 =3= suedecoq[(15679)r4c123/r4c5(19)/r5c3(57)] -6- r4c7 =6= r6c7 -6- r6c3 -8- r5c2 -9- r4c1 => r4c1<>9

When the elimination of a Sue de Coq ("SdC") pattern is in the SdC pattern itself, even an almost SdC pattern, IMO it's a safe bet that there will always be a smaller pattern. Using all but two of those same cells, we have a simpler chain ...

r4c1 -9- als:r4c25 -5- als:[r456c3,r5c2] -9- r4c1 ==> r4c1<>9

... also known as the ALS xz-rule. However, the almost SdC is still an interesting POV.

[DonM]

But for the 3 in r4c1, the basic Sue De Coq pattern is present: the core blue cells (an aals with 1,5,6,7,9 in 3 cells), the brown cell A with 5,7 and the green cell C with 1,9. The logic is straightforward: If not 3 in r4c1 then the Sue De Coq is true and any of the circled green cells are valid weak link ‘targets’. In this case a relatively simple chain eliminates the 9 in r4c1:

aic:
(3)r4c1 = suedecoq[(15679)r4c123/r4c5(19)/r5c3(57)] - (6)r4c7 = r6c7-(6=8)r6c3 - (8=9)r4c2 => r4c1<>9
nice loop:
r4c1 -9- r4c1 =3= suedecoq[(15679)r4c123/r4c5(19)/r5c3(57)] -6- r4c7 =6= r6c7 -6- r6c3 -8- r5c2 -9- r4c1 => r4c1<>9

When the elimination of a Sue de Coq ("SdC") pattern is in the SdC pattern itself, even an almost SdC pattern, IMO it's a safe bet that there will always be a smaller pattern. Using all but two of those same cells, we have a simpler chain ...

r4c1 -9- als:r4c25 -5- als:[r456c3,r5c2] -9- r4c1 ==> r4c1<>9

... also known as the ALS xz-rule. However, the almost SdC is still an interesting POV.

Regarding the 'safe bet'- likely true for the most part, but I'm not willing to concede that for all forms & all parts of the a-SDC just yet. In addition, I think there may be other uses for the a-SDC. At the very least, since I look for SDC anyway, if I come up with an a-SDC and a nice elimination thereof, I might just go with that instead of looking for an alternative partly since the alternative my not be all that much simpler- eg. looking at the 2 chains above, the one with 2 als's is simpler than the one with one a-SDC but perhaps not strikingly so.

fwiw: I had mentioned in the opening post that I had an alternate for the 1st a-SDC:

hp(19)r4c25=(5)r4c2-als(5=67)r45c3-(6=8)r6c3-(8=9)r4c2 => r4c1<>9 (seems to follow a similar course to yours above).

[David P Bird]

A plain SdC can be written as a series of up to 5 AICs with simple ALSs (one for each digit eliminated). Clearly in these circumstances it's much more elegant to replace 5 lines of notation with one, and the SdC representation should be favoured.

When we get to an Almost SdC we'll usually be able to eliminate only one of the five digits so the simple chain will be superior. As I said, I have yet to find an Almost SdC exclusion which can't be so simplified. One exceptional case I can envisage is when group nodes are involved that are split across two box-line intersections (as can happen when fish fins are incorporated in AICs). We have millions of possible puzzles so there must be a few out there, but I'm sure they'll be very low frequency.

Don, a good start for you to make your case would be to see if you can find an instance of an Almost SdC that will eliminate more than one of the usual SdC victims. There's then a good chance your single step would either take two AICs employing simpler ALSs or be incapable of being replicated altogether.

[Luke]

Does anyone mind if I start over on this? I can't be the only one out there who found this a tad confusing (I hope...)



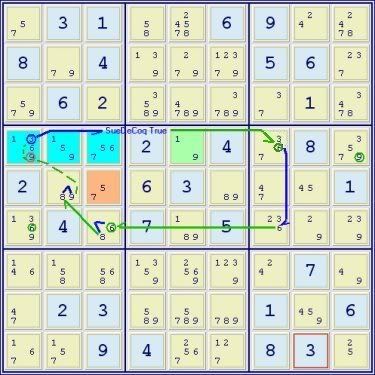
Here's what I've gathered so far, in POE notation (Plain Ole English.)

- Blue cells = core; brown and green = a and b respectively.
- Blue circle = extra candidate.
- Blue links = strong, green = weak.
- The reason [3 = The SdC] is because either the 3 is true or the SdC is true.
- This means that [3 = The SdC] can be used as a strong link in an AIC or Nice Loop.
- The green circled candidates represent possible targets for weak links to follow after [3 = The SdC].
- The loop begins and ends with a weak discontinuity on 9, so r4c1<>9.

Have I the basics right?
Why's the 6 in r6c1 green circled and not the 9? Or the 9 in r4c9 and not the 5 or 7 in r4 box 6?
Can the "extra candidate" also be in cells a or b?

My reality check: Finding a naked Sue de Coq is always cool, but not that easy. An "almost" is tougher, albeit perhaps more common. Finding a useful loop off an "almost" ups the ante once again into the "are you kidding me" range. I guess only time/practice will tell.

That said, thanks to Don for your great effort here. I've learned a lot, and thanks to ronk, hobiwan, Glyn and others for pointing out useful variations and nuance.

[Glyn]

Luke451 Some of the answers to your questions.
r4c5 contains (1 or 9) so (1 and 9) can't be locked in r4c123. Hence no green circle round those in the rest of b4.
Likewise r5v3 contains (5 or 7) so (5 and 7) cant be locked in r4c123 so no circles round those in the rest of r4.
Only the green circles are targets of the Sue de Coq.

I would think the extra candidate scuppering the Sue de Coq can be anywhere as long as it leads to common eliminations with the Sue de Coq.

Incidentally in the figure we could have linked the 3 in r4c1 directly to the 6 in r6c3, would have made box 4 a bit messy though.

[DonM]

- The reason [3 = The SdC] is because either the 3 is true or the SdC is true.
- This means that [3 = The SdC] can be used as a strong link in an AIC or Nice Loop.
- The green circled candidates represent possible targets for weak links to follow after [3 = The SdC].
- The loop begins and ends with a weak discontinuity on 9, so r4c1<>9.

Have I the basics right?

Absolutely, and to understand this is to understand virtually any other almost pattern. This is a good example where I think graphics-based examples decrease the learning curve.

Why's the 6 in r6c1 green circled and not the 9? Or the 9 in r4c9 and not the 5 or 7 in r4 box 6?
Can the "extra candidate" also be in cells a or b?

I look on the eliminations from the cells A & B in a regular SDC as based on the same logic as that of simple naked pairs which is why the 9 could not be eliminated from anywhere but row 4 or the 5 or 7 anywhere but in box 6 (though in this case there are no 5s or 7s in box 6 to eliminate). In answer to the last question, off the top of my head, I don't think so given the logic, but there are so many aberrations of SDC that I could be wrong. Speaking of SDC variations: fwiw: you can have an aaals-type SDC (ie. say, 6 digit values in 3 cells) where there are 2 bivalue cells in the line or box where the 2nd cell, outside of the traditional A & B, contains both the extra digit that would ordinarily have been in the gold cell C and the 'extra' cell from the core.

My reality check: Finding a naked Sue de Coq is always cool, but not that easy. An "almost" is tougher, albeit perhaps more common. Finding a useful loop off an "almost" ups the ante once again into the "are you kidding me" range. I guess only time/practice will tell. That said, thanks to Don for your great effort here. I've learned a lot, and thanks to ronk, hobiwan, Glyn and others for pointing out useful variations and nuance.

If one concentrates on understanding the generic SDC and looking for it in all puzzles, then eventually, not only is it easy to find, but you also get to the point where the additions/exceptions just naturally come along for the ride. My first step is a quick look for an aals or aaals in a row or column in a box and, if so, then for any bivalue cells at all in that row/column or box. If no bivalue cells then its on to another box- takes no more than a few seconds. (It's just a few more seconds to see if any bivalue cells that were present fill the bill).

The usefulness of SDC likely depends on one's perpective. Over at Eureka, between a fun (well, I think it's fun ) challenge puzzle 'competition' I've been running from time to time and the weekly Extreme puzzles, we manually solve puzzles from about ER 8.3 to 9.0. Finding a SDC, in this situation is like gold and, personally & parenthetically, I find it easier to find a SDC than the combination of ALSs that might be necessary to find to achieve the same eliminations. Also, under this scenario, I'm going to continue to look for almost-SDCs to see if they occasionally make this sort of solving easier- from the point of view that even if they don't end up providing an elimination (repeating myself, I know) that can't be achieved any other way, they might be a like a menu of possible eliminations without my having to look any further for alternatives that accomplish the same thing. It's hard to tell at this stage. I do know that at that level of puzzle difficulty every little advantage helps or may help.