The New Sudoku Players' Forum

[HATMAN]

Sujiko 1

I've just published this puzzle on the assassin site, however in the creating my next one the following question came to mind:

If the 25 sums give a feasible solution is it automatically unique in all cases? i.e. necessary equals sufficient.

Whether it is solvable without heavy number crunching is a separate matter - although even then the analysis is only of spreadsheet level.

I am currently attempting to create a counter example.

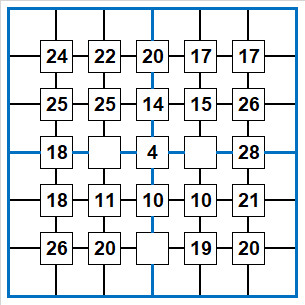
Puzzle: Sujiko 1

I've been doing these in the (UK) Sunday Telegraph - with difficulty. Hence I thought to create them so as to understand the solution methodology better.

The clues are the sum of the adjacent four squares.
The numbers 1-9 cannot repeat in the blue nonets.
Numbers can repeat in rows and columns.
Numbers can repeat in clue sums.

Given the central clue this puzzle is not that hard, hence I have left out a few sums. I am never sure whether to do this as leaving out clues makes the solution path clearer, if more difficult.

[tarek]

This is like sudokakuro ... it crosses the boundaries into killer as well!!! Haven’t tried it yet!

Tarek

[creint]

Less than 5 minutes(should be 1-2) inputtime into my solver, solvetime: ~0.38 seconds. With Z3 ~0.13 seconds.
Solving is often easier than generating.

Has a single solution:

Hidden Text: Show

6 4 2 6 4 3
5 9 7 5 2 8
3 8 1 1 7 9
4 3 1 1 4 8
9 2 5 3 2 7
8 7 6 9 5 6

[HATMAN]

So you have a very flexible solver creint.

As a counter example this has multiple solutions, however what I have found so far are just symmetry variations based on one nonet solution repeated.

[Mathimagics]

I was actually working on a Sudoku variant just like this when I got diverted by the LCT project back onto vanilla Sudoku matters.

But I was using a full 9x9 grid with the standard row/col/box rules. Then it becomes very much like a Killer, but with the multiple overlapping cages.

I was at the point where I was trying to decide whether to make them "true" cages (no repeating digits) or not when LCT took over. I will return to this when I can, meanwhile creint might like to explore this question (he does indeed have a very flexible solver!).

[HATMAN]

I've been spending too much time on counter examples but it is definitely not unique when feasible in all cases, but I am sure that in the vast majority when clues are not symmetrical it is.
Where the 25 sums are all 20 then then the four 20 in a nonet give seven solutions plus symmetries:
C1 C2 C3 C4 C5 C6 C7 C8 C9
1 8 3 9 2 7 4 5 6
1 6 7 9 4 3 2 5 8
3 5 2 8 4 9 7 1 6
1 6 7 8 5 2 3 4 9
2 5 8 7 6 1 3 4 9
3 2 7 9 6 5 4 1 8
4 3 7 5 8 2 6 1 9

So centre values of 1 3 7 9 have no solutions 2 5 8 have a single solution and 4 and 6 have two slightly linked solutions.

Using the 5 centre set in the 4 nonets we can form a solution with the four centre cells 1991 and another with four centre cells 3773, plus of course their symmetries.

There may be other solutions using mix and match but as I am doing this semi-manually, life is too short.

[Mathimagics]

As a general rule, valid sums will mostly give rise to multiple solutions. Unique solutions tend to be the exceptions ...

The more sums there are with very low or high values, then the more likely it is that the solutions will be unique.

[HATMAN]

Mathimagics you have to be careful with general rules. The best one that I remember in the Sudoku area was from Mike_Japan way back on the DJape site:

For very hard killers when you get stuck and you are interested in a cell with multiple values chose the one that gives the most possibilities.

Its success levels were very high which, as I remember, infuriated Udosuk.

[Mathimagics]

As a general rule, one has to be careful with general rules ...