The New Sudoku Players' Forum

[Mathimagics]

.
Things go such better when you have a working fast solver!

Found a 3-clue NC+:

Code: Select all

 +-------+-------+-------+
 | . 1 . | . . . | . . . |
 | . . 4 | . . . | . . . |
 | . . . | . . . | . . . |
 +-------+-------+-------+
 | . . . | . . . | . . . |
 | . . . | . . . | . . . |
 | 5 . . | . . . | . . . |
 +-------+-------+-------+
 | . . . | . . . | . . . |
 | . . . | . . . | . . . |
 | . . . | . . . | . . . |
 +-------+-------+-------+


[tarek]

.
Found a 3-clue NC+:

Code: Select all

 +-------+-------+-------+
 | . 1 . | . . . | . . . |
 | . . 4 | . . . | . . . |
 | . . . | . . . | . . . |
 +-------+-------+-------+
 | . . . | . . . | . . . |
 | . . . | . . . | . . . |
 | 5 . . | . . . | . . . |
 +-------+-------+-------+
 | . . . | . . . | . . . |
 | . . . | . . . | . . . |
 | . . . | . . . | . . . |
 +-------+-------+-------+


Confirmed & congratulations. Solution:

Code: Select all

+-------+-------+-------+
| 6 1 8 | 4 2 9 | 5 7 3 |
| 3 7 4 | 1 8 5 | 9 2 6 |
| 9 5 2 | 6 3 7 | 4 8 1 |
+-------+-------+-------+
| 2 8 6 | 9 7 4 | 1 3 5 |
| 7 4 1 | 3 5 2 | 8 6 9 |
| 5 9 3 | 8 1 6 | 2 4 7 |
+-------+-------+-------+
| 8 3 5 | 2 6 1 | 7 9 4 |
| 1 6 9 | 7 4 8 | 3 5 2 |
| 4 2 7 | 5 9 3 | 6 1 8 |
+-------+-------+-------+

[tarek]

So I'm guessing that you would have had to go through (18,569 x 81 x 80 x 79 / 6 ) 3 clue puzzles !!

It means that you have already done the same process for 2 clue cases & the 1 clue cases as well


tarek

[coloin]

Well ... i couldnt solve the 5 clue puzzle by hand ...... didnt want to guess.
Suppose it really was an ER=12.0

[Mathimagics]

So I'm guessing that you would have had to go through (18,569 x 81 x 80 x 79 / 6 ) 3 clue puzzles !!

More or less. Well, less, I think. I am not sure where that 18,569 figure comes from. 3-cell selections is done 81*80*79/6 ways, yes, but surely 3 clues can only have 729 = 9^3 different value settings?

Anyhow, there are definitely no 2-clue NC+ puzzles, so 3 is definitely the minimum.

And if 2-clue puzzles don't exist for NC+ then they certainly won't be found for NC.

I tried adding a dimension (eg SudokuP), even 1.2 dimensions (SudokuPX), but no cigar! We just get increasing numbers of 3-clue puzzles.


PS: nobody needs to tell me that the cell-selection and value-selections are mostly invalid, and that there are clever ways to reduce the number of puzzles that are actually tested. I prefer to let the solver deal with that nonsense, it's a lot smarter than me. This, ladies and gentlemen, is brute force in its most primitive form, and it ain't pretty!

[tarek]

So I'm guessing that you would have had to go through (18,569 x 81 x 80 x 79 / 6 ) 3 clue puzzles !!

More or less. Well, less, I think. I am not sure where that 18,569 figure comes from. 3-cell selections is done 81*80*79/6 ways, yes, but surely 3 clues can only have 729 = 9^3 different value settings?

That is True. 18,569 was the the number of ED grids you provided but 729 looks much better it just tells how well placed these clues need to be!

Well ... i couldnt solve the 5 clue puzzle by hand ...... didnt want to guess.
Suppose it really was an ER=12.0

There was a disclaimer about approaching with caution!!! I did post later down that page some Easy ones.

PS: nobody needs to tell me that the cell-selection and value-selections are mostly invalid, and that there are clever ways to reduce the number of puzzles that are actually tested. I prefer to let the solver deal with that nonsense, it's a lot smarter than me. This, ladies and gentlemen, is brute force in its most primitive form, and it ain't pretty!

Because of the 8 way symmetries amongst others


Tarek

[Mathimagics]

You just couldn't help yourself, tarek, could you!!!

You just earned a Sybil Fawlty Award nomination

[Mathimagics]

.
Ok, I made one final attempt to find a 2-givens NC+ puzzle.

This is one of just 29 14 grids in the NC+ ED catalog (18,569 grids 12,263) that is both SudokuPX and has toroidal adjacency property. Toroidal simply means (R1, R9) are adjacent, as are (C1, C9). Thus every cell has 4 adjacent cells. Note that this extended adjacency is generic, ie can be applied to any FP case.

Code: Select all

 +-------+-------+-------+
 | 1 3 6 | 2 8 5 | 7 9 4 |
 | 8 5 2 | 9 4 7 | 3 6 1 |
 | 4 7 9 | 6 1 3 | 5 2 8 |
 +-------+-------+-------+
 | 9 4 7 | 3 6 1 | 8 5 2 |
 | 6 1 3 | 5 2 8 | 4 7 9 |
 | 2 8 5 | 7 9 4 | 1 3 6 |
 +-------+-------+-------+
 | 5 2 8 | 4 7 9 | 6 1 3 |
 | 7 9 4 | 1 3 6 | 2 8 5 |
 | 3 6 1 | 8 5 2 | 9 4 7 |
 +-------+-------+-------+


Here is a 3-given puzzle, but not for the same grid. tarek clearly has nothing better to do, so he can P&P it and post the solution. No assistance please!

Code: Select all

 +-------+-------+-------+
 | . . . | . . . | . . . |
 | . . . | . . . | . . . |
 | . . . | 8 . . | . . . |
 +-------+-------+-------+
 | . . . | . . . | . . . |
 | . . . | . . . | . . . |
 | . . . | . . . | . . . |
 +-------+-------+-------+
 | . . . | . . . | . . . |
 | . . . | . 3 . | . . 5 |
 | . . . | . . . | . . . |
 +-------+-------+-------+


Now we have fewer ED grids in this set, only 29, but every one of them has 3-clue puzzles galore.

And still there are no 2-clue puzzles!

That's it for NC, I think.

Now we just want a truth-table. But can we handle the truth-table? (settle down, Jack)

[tarek]

tarek clearly has nothing better to do, so he can P&P it and post the solution. No assistance please!

Maybe if you made it symmetrical

Code: Select all

cNC PX Toroid
 +-------+-------+-------+
| . . . | . . . | . . . |
| . . . | . . . | . . . |
| . . . | . . . | . . 1 |
+-------+-------+-------+
| . . . | . . . | . . . |
| 2 . . | . . . | . . . |
| . . . | . . . | . . . |
+-------+-------+-------+
| . . . | . . . | . . 7 |
| . . . | . . . | . . . |
| . . . | . . . | . . . |
+-------+-------+-------+

+-------+-------+-------+
| . . . | . . . | . . . |
| . . . | . . . | . . . |
| . . . | . . . | . . . |
+-------+-------+-------+
| . . . | . 1 . | . . . |
| . . . | . . . | . . . |
| . . . | . . . | . . . |
+-------+-------+-------+
| . . . | . . . | . . . |
| . 4 . | . . . | . 6 . |
| . . . | . . . | . . . |
+-------+-------+-------+

+-------+-------+-------+
| . . . | . . . | . . . |
| . . . | . . . | . . . |
| . . . | . . . | . . . |
+-------+-------+-------+
| . . . | . . . | . . . |
| . . . | . . . | . . 1 |
| . . . | . . . | . . . |
+-------+-------+-------+
| . . . | . . . | . . . |
| . . . | . . . | . 3 . |
| . . . | . 7 . | . . . |
+-------+-------+-------+


tarek

[Mathimagics]

Symmetry is SO last year …
=======================

Ok, you want the truth about tables?

Some basic facts …

No row can have more than 5 x 1's in it (4 FPs + the diagonal entry). Here's a TT that restricts the value 1 to neighbours {7,8,9}, so there are 6 FPs, ie 6 x 1's in row 1 and col 1. Now you can make a Latin Square that conforms to these restrictions, as shown in the 2nd grid, but you can`t make a Sudoku!

In fact you can add one more FP in row 1 and still make a LS, in which 1 is only adjacent to two pairs of values (7 x 1's in row 1 if the TT), as shown in the 3rd grid. The added FP is (1,8).

Code: Select all

 1 1 1 1 1 1 0 0 0   |   1 7 2 3 4 5 6 8 9   |   1 7 2 3 4 5 6 8 9
 1 1 0 0 0 0 0 0 0   |   7 1 9 2 3 4 5 6 8   |   7 8 6 2 3 4 5 9 1
 1 0 1 0 0 0 0 0 0   |   5 8 6 9 2 3 4 7 1   |   6 4 5 8 2 3 9 1 7
 1 0 0 1 0 0 0 0 0   |   4 6 3 5 9 2 8 1 7   |   4 2 3 5 6 9 1 7 8
 1 0 0 0 1 0 0 0 0   |   2 3 8 4 6 7 1 9 5   |   8 3 4 6 9 1 7 2 5
 1 0 0 0 0 1 0 0 0   |   3 9 1 8 5 6 7 2 4   |   2 5 8 9 1 7 3 4 6
 0 0 0 0 0 0 1 0 0   |   6 5 7 1 8 9 2 4 3   |   5 6 9 1 7 2 8 3 4
 0 0 0 0 0 0 0 1 0   |   9 2 4 7 1 8 3 5 6   |   3 9 1 7 5 8 4 6 2
 0 0 0 0 0 0 0 0 1   |   8 4 5 6 7 1 9 3 2   |   9 1 7 4 8 6 2 5 3


Since the table is symmetric about the diagonal, that means we can have at most 18 FP`s all up.

[Mathimagics]

Note that the # of ED NC+ grids reported previously was incorrect. The true figure is 12,263. This was spotted by blue (thanks!). It seems that I had omitted one of the relabelling symmetries in the CF function.

[tarek]

.
This is one of just 29 grids in the NC+ ED catalog (18,569 grids) that is both SudokuPX and has toroidal adjacency property.

As your cNC ED grid number were revised, I think I've got the cNC PX Toroid ED grids revised to 14

[Mathimagics]

I have found a 2-clue FP puzzle for a SudokuX.

2-clue SudokuX-FP: Show

Code: Select all

 +-------+-------+-------+
 | . . . | . . 9 | . . . |
 | . . . | . . . | . . . |
 | . . . | . . . | . . . |
 +-------+-------+-------+
 | . . . | . . . | . . . |
 | . . . | . . . | 6 . . |
 | . . . | . . . | . . . |
 +-------+-------+-------+
 | . . . | . . . | . . . |
 | . . . | . . . | . . . |
 | . . . | . . . | . . . |
 +-------+-------+-------+


Solution: Show

Code: Select all

 +-------+-------+-------+
 | 3 2 1 | 4 6 9 | 8 7 5 |
 | 8 7 5 | 1 2 3 | 9 6 4 |
 | 9 6 4 | 5 7 8 | 3 2 1 |
 +-------+-------+-------+
 | 6 4 8 | 9 5 7 | 2 1 3 |
 | 7 5 9 | 3 1 2 | 6 4 8 |
 | 2 1 3 | 8 4 6 | 7 5 9 |
 +-------+-------+-------+
 | 1 3 2 | 7 8 4 | 5 9 6 |
 | 5 9 6 | 2 3 1 | 4 8 7 |
 | 4 8 7 | 6 9 5 | 1 3 2 |
 +-------+-------+-------+


It is perhaps of interest to describe the search process, as it involves a little Graph Theory, and I happen to like that very much!

As I mentioned above, the 18-FP truth-table seemed the obvious place to start looking. This is the maximum number of FP's that can be used, and so gives the maximum potential for restricting the applicable grid solution space.

The first question to answer was, how many TT18's are there, or more importantly, how many ED flavours are there? Consider this example:

Code: Select all

   . . . . . X X X X
   . . . . X . X X X
   . . . X . . X X X
   . . X . X X . . X
   . X . X . X . X .
   X . . X X . X . .
   X X X . . X . . .
   X X X . X . . . .
   X X X X . . . . .


Now if we invert the dots and the X's (excluding the main diagonal), then this becomes an adjacency table (as against a forbidden pair table), and one that has the same properties. There are still 4 X's in each row and column. Adjacency tables are just graphs in another form. And since each vertex has 4 edges joining it to other vertices, our TT is a 9V 4-regular graph, and we know quite a bit about these guys.

There are only 16 ED graphs in this category, and so there are just 16 flavours of TT18's. In my list the TT above is #5.

AG5 graph: Show

Adjacency Graph AG5

09_4_3-5.gif (2.68 KiB) Viewed 1132 times

Now, it turns out that only 3 of these 16 adjacency graphs can be used, since the rest do not correspond to any Sudoku grids. 9 of them do not allow the completion of a 3x3 box, and 4 more are found to be incompletable, that is, there are boxes but they can't be assembled to form a valid grid. The only valid ones are the final 3 in my list, ie AG14, AG15, and AG16. (Note: validity here refers to satisfying the TT, not just getting a valid Sudoku grid).

The valid AGs: Show

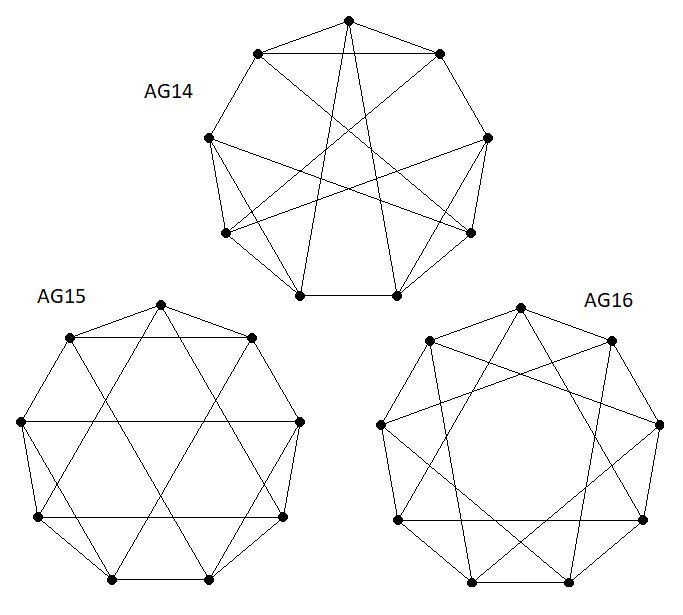
Valid AG's

AG14-15-16.png (18.69 KiB) Viewed 1132 times

It is interesting to note how "regular" these are compared to AG5, and there is probably something more to be learned there. But now we have just 3 TT18's as candidates, and so can use the brute-force clue-pattern method to search for low-clue puzzles for each case.

AG14 disappoints, it produces no 3-clue puzzles, but both AG15 and AG16 produce 3-clue puzzles in standard Sudoku form. Since we already know that the NC case has no 3-clue puzzles, this is progress! We find millions of 3-clue puzzles for AG15 and AG16, but alas, no 2-clue puzzles. So we look to add constraints, and by starting with SudokuX, are rewarded with an abundance of 2-clue puzzles (53,088).

None for AG16 though. AG15 is the only TT18 which yields 2-clue puzzles.

The next step is to consider other TT's with less than 18 FP's. Can they produce 2-clue puzzles?

And does the 1-clue puzzle exist in this FP form?

Watch this space

[Mathimagics]

As your cNC ED grid number were revised, I think I've got the cNC PX Toroid ED grids revised to 14

Thank you, tarek. The bug in my CF function means that any figure I had previously involving NC+ was wrong. I have corrected the figures above.

[Mathimagics]

.
A little diversion, a puzzle if you like. Consider this run log:

Code: Select all

D:\SudokuFP\FindMCX 2

01:14:15:  <start>
01:14:25:  2C combns =  3240
01:14:25:  <done> np = 53088

D:\SudokuNC>FindMCX 2

00:15:32:  <start>
13:19:51:  2C combns =  3240
13:19:53:  <done> np =  1056


FindMC is my little brute-force clue pattern tester. FindMCX is simply the version that uses SudokuX mode. We are testing here just for 2-clue puzzles, so exactly 3240 x 9^2 solver invocations are involved.

Now, why do you think the first job takes only 10 seconds, but the second one takes 13 excruciating hours (nearly 5000 times longer)?

A virtual cigar for the first correct answer (NB: blue is excluded )