The New Sudoku Players' Forum

[Mathimagics]

.
Here is puzzle which is Sudoku with a Kakuro twist, hence the name SudoKakuro (pun intended!)

The clues (where given) for any cell are the sum of the cell's immediate neighbours (ie: orthogonally adjacent cell). Corner cells have only 2 neighbours, other edge cells have 3, and all the other cells have 4.

Note that the sum does NOT include the cell itself, so a clue tells you nothing about the cell to which it applies, which is itself a little unusual.

Also note that, in the Kakuro tradition, only combinations of distinct digits are allowed, and this means that the solution will always be a SudokuDP (Anti-King Sudoku) grid. That is, no two diagonally-adjacent cells can have the same value.

[ EDIT ] creint reminded me of the need to clarify this. This property of solution grids (no diagonal pairs have same value) is ALWAYS applicable. So even when sum clues are omitted, which will normally be the case, this rule still applies.

Puzzles that are fully specified (all neighbour sums are provided), as in this first example, are the easiest, but the real fun will begin when we start removing clues!

SudoKakuro Example #1

SK-Example1.jpg (41.45 KiB) Viewed 1415 times

Solution:

Hidden Text: Show

Code: Select all

  +-------+-------+-------+
  | 7 6 9 | 4 5 1 | 2 3 8 |
  | 1 5 2 | 8 3 6 | 9 7 4 |
  | 8 3 4 | 9 2 7 | 1 5 6 |
  +-------+-------+-------+
  | 2 1 6 | 7 4 5 | 8 9 3 |
  | 3 7 5 | 1 8 9 | 4 6 2 |
  | 9 4 8 | 3 6 2 | 7 1 5 |
  +-------+-------+-------+
  | 6 2 7 | 5 1 8 | 3 4 9 |
  | 5 9 3 | 2 7 4 | 6 8 1 |
  | 4 8 1 | 6 9 3 | 5 2 7 |
  +-------+-------+-------+


[Mathimagics]

.
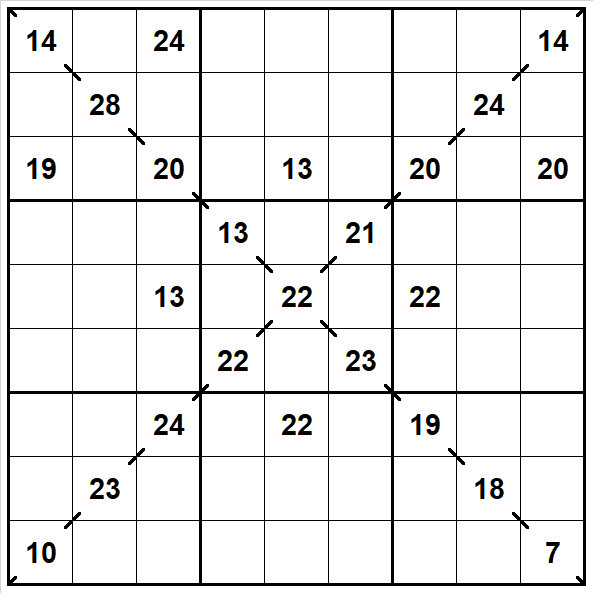
To get started, look for sums that are unique for the applicable length, ie can only be formed one way. I have provided a table of possible sums for 2, 3 and 4 neighbours below.

For example (r9,c9) in the example above has the clue 3, so (r8,c9) and (r9,c8) must be {1,2}, so this clue provides a naked pair, ie {1,2} can be eliminated as values for the other cells in box 9.

The clue 10 in (r6,c7) also implies that all neighbours have values {1,2,3,4}. This gives a "nearly-naked quadruple". It's not completely naked since the neighbours are in different boxes. If you find a unique-sum clue in a central box position, that's a bonus.

Another less obvious method is to look for clues that are two cells apart, and have maximum difference (ie one high value, one low value). Clues in adjacent cells have neighbour sets that don't interesect, but clues that are two cells apart (in row or column) share a neighbour. If the clues differ sufficiently, this can tell you much about the shared neighbour cell (the one between). For example, if the clues are 29 and 11, then the shared cell must be 5.

Table of digit-combinations:

Hidden Text: Show

Code: Select all

 3: 12
 4: 13
 5: 14, 23
 6: 15, 24
 7: 16, 25, 34
 8: 17, 26, 35
 9: 18, 27, 36, 45
10: 19, 28, 37, 46
11: 29, 38, 47, 56
12: 39, 48, 57
13: 49, 58, 67
14: 59, 68
15: 69, 78
16: 79
17: 89

 6: 123
 7: 124
 8: 125, 134
 9: 126, 135, 234
10: 127, 136, 145, 235
11: 128, 137, 146, 236, 245
12: 129, 138, 147, 156, 237, 246, 345
13: 139, 148, 157, 238, 247, 256, 346
14: 149, 158, 167, 239, 248, 257, 347, 356
15: 159, 168, 249, 258, 267, 348, 357, 456
16: 169, 178, 259, 268, 349, 358, 367, 457
17: 179, 269, 278, 359, 368, 458, 467
18: 189, 279, 369, 378, 459, 468, 567
19: 289, 379, 469, 478, 568
20: 389, 479, 569, 578
21: 489, 579, 678
22: 589, 679
23: 689
24: 789


10: 1234
11: 1235
12: 1236, 1245
13: 1237, 1246, 1345
14: 1238, 1247, 1256, 1346, 2345
15: 1239, 1248, 1257, 1347, 1356, 2346
16: 1249, 1258, 1267, 1348, 1357, 1456, 2347, 2356
17: 1259, 1268, 1349, 1358, 1367, 1457, 2348, 2357, 2456
18: 1269, 1278, 1359, 1368, 1458, 1467, 2349, 2358, 2367, 2457, 3456
19: 1279, 1369, 1378, 1459, 1468, 1567, 2359, 2368, 2458, 2467, 3457
20: 1289, 1379, 1469, 1478, 1568, 2369, 2378, 2459, 2468, 2567, 3458, 3467
21: 1389, 1479, 1569, 1578, 2379, 2469, 2478, 2568, 3459, 3468, 3567
22: 1489, 1579, 1678, 2389, 2479, 2569, 2578, 3469, 3478, 3568, 4567
23: 1589, 1679, 2489, 2579, 2678, 3479, 3569, 3578, 4568
24: 1689, 2589, 2679, 3489, 3579, 3678, 4569, 4578
25: 1789, 2689, 3589, 3679, 4579, 4678
26: 2789, 3689, 4589, 4679, 5678
27: 3789, 4689, 5679
28: 4789, 5689
29: 5789
30: 6789


[Mathimagics]

.
This puzzle has 50 clues. It should be relatively easy, but that's just a guess. It will certainly be easier than the examples following!

Image:

Hidden Text: Show

SudoKakuro Example #2

SK-Example2.jpg (33.59 KiB) Viewed 1413 times

Solution:

Hidden Text: Show

Code: Select all

  +-------+-------+-------+
  | 2 1 7 | 3 9 5 | 4 6 8 |
  | 8 4 5 | 1 6 2 | 7 3 9 |
  | 3 9 6 | 7 4 8 | 5 2 1 |
  +-------+-------+-------+
  | 7 5 3 | 8 2 1 | 9 4 6 |
  | 9 8 2 | 4 7 6 | 3 1 5 |
  | 4 6 1 | 5 3 9 | 2 8 7 |
  +-------+-------+-------+
  | 1 3 4 | 9 8 7 | 6 5 2 |
  | 6 7 8 | 2 5 4 | 1 9 3 |
  | 5 2 9 | 6 1 3 | 8 7 4 |
  +-------+-------+-------+


[Mathimagics]

.
This one will be much more challenging, only 25 clues:

Image:

Hidden Text: Show

SudoKakuro Example #3

SK-Example3.jpg (27.23 KiB) Viewed 1411 times

Solution:

Hidden Text: Show

Code: Select all

  +-------+-------+-------+
  | 8 4 3 | 9 5 6 | 1 2 7 |
  | 9 7 5 | 1 8 2 | 4 3 6 |
  | 2 1 6 | 7 4 3 | 8 5 9 |
  +-------+-------+-------+
  | 7 3 9 | 5 6 1 | 2 4 8 |
  | 6 8 2 | 4 3 7 | 5 9 1 |
  | 4 5 1 | 8 2 9 | 6 7 3 |
  +-------+-------+-------+
  | 1 9 4 | 6 7 5 | 3 8 2 |
  | 3 6 8 | 2 9 4 | 7 1 5 |
  | 5 2 7 | 3 1 8 | 9 6 4 |
  +-------+-------+-------+



[Mathimagics]

.
This is just to demonstrate the enormous scope for difficulty level. It has only 13 clues, yet the solution is unique.

My solver is still too slow to tell whether less clues are possible.

Puzzle image:

Hidden Text: Show

SudoKakuro Example #4 (a brute!)

SK-Example4-Killer.jpg (22.8 KiB) Viewed 1410 times

Solution:

Hidden Text: Show

Code: Select all

  +-------+-------+-------+
  | 3 4 7 | 8 9 5 | 1 2 6 |
  | 8 5 9 | 2 1 6 | 4 3 7 |
  | 1 2 6 | 7 4 3 | 9 8 5 |
  +-------+-------+-------+
  | 6 7 5 | 3 8 1 | 2 4 9 |
  | 9 8 2 | 4 6 7 | 3 5 1 |
  | 4 1 3 | 5 2 9 | 6 7 8 |
  +-------+-------+-------+
  | 7 6 4 | 1 3 8 | 5 9 2 |
  | 2 9 8 | 6 5 4 | 7 1 3 |
  | 5 3 1 | 9 7 2 | 8 6 4 |
  +-------+-------+-------+



[tarek]

This variant is beautiful. I like the idea very much. This one specifically works well for newspapers too

This would mean an easy transition for you with your programming skills to Killer sudoku territory. We are all greedy here, so with your momentum here, It will be nice to see a slover/generator for everybody to use and enjoy!!!

I’ll say it again MM. ..., Bravo

Tarek

[Mathimagics]

.
Hello tarek,

Thanks very much for your positive feedback!

Presumably the solver/generator you refer to is a "Sudoku Killer" app (for Windows)? I could perhaps do that ... I always did like doing those puzzles (back in the day when I actually DID puzzles! )

Cheers!

[creint]

Can you post a template so it becomes easier to paste into solvers?
Manually adding this into my solver takes too much time with fully specified grids.

Also note that, in the Kakuro tradition, only combinations of distinct digits are allowed, and this means that the solution will always be a SudokuDP (Anti-King Sudoku) grid. That is, no two diagonally-adjacent cells can have the same value.

Maybe this was not clear: This full Anti-King rule only applies on grids that are fully specified.

[Mathimagics]

Maybe this was not clear: This full Anti-King rule only applies on grids that are fully specified.

The solver should assume the DP (Anti-King) rule always applies, the solution grid will always have this property. I have added a comment to that effect above. I had considerd making it only apply to the clues given, but decided this might be confusing for some.

Can you post a template so it becomes easier to paste into solvers?

Do you mean a template for the sums?

Is this suitable?

Hidden Text: Show

Code: Select all

Example #2:
  . 13  9  . 14 15 18 15 15
  9  .  .  . 16 26 14  . 12
 24 18 24 19 23 12  .  .  .
  .  .  . 16 20 25 13  . 10
 19 22  . 22 15 20 18 20  .
 16  . 17  . 29  . 26  .  .
  . 18  .  . 24 27  .  .  .
 13  . 22  .  . 16 27 16 15
  . 21 16  .  . 13  . 21 10

Example #3:
 13 18  .  9 23  8  .  .  .
  .  .  .  .  .  .  .  .  .
 17  . 22  . 24  .  .  .  .
  . 25 16  .  . 18 18  .  .
  . 16 22 18 19  . 24  .  .
  .  .  .  .  .  . 24  .  .
  . 16 24  .  .  .  .  . 16
  .  .  . 26  .  .  .  .  .
  .  .  . 10  .  . 21 14  .

Example #4:
  .  .  . 18  .  .  .  .  .
  .  .  .  . 21 13  .  .  .
 16  .  .  .  .  .  .  .  .
  .  . 18  .  .  .  .  . 10
  .  .  .  . 21  .  .  .  .
  .  . 12 10 23  . 24  . 10
  .  .  .  .  .  .  .  .  .
  .  .  .  .  .  .  .  .  .
  .  .  .  . 16  .  .  .  .


[Mathimagics]

.
Here are 8 more puzzles with symmetric clue patterns, in a simple text format showing the clues for each cell.

They are given in (approximate) order of difficulty (based on solver iterations).

Puzzles:

Hidden Text: Show

Code: Select all


SK-17CS-004:
  5  . 21  .  .  . 19  .  9
  .  .  .  .  .  .  .  .  .
 15  . 30  .  .  . 18  . 22
  .  .  .  .  .  .  .  .  .
  .  .  .  . 20  .  .  .  .
  .  .  .  .  .  .  .  .  .
 13  . 19  .  .  . 27  . 23
  .  .  .  .  .  .  .  .  .
  6  .  7  .  .  . 14  .  7

SK-17CS-003:
  . 14  .  .  .  .  . 22  .
 16  . 22  .  .  . 27  . 14
  . 23  .  .  .  .  . 24  .
  .  .  .  .  .  .  .  .  .
  .  .  .  . 25  .  .  .  .
  .  .  .  .  .  .  .  .  .
  . 24  .  .  .  .  . 13  .
 16  . 28  .  .  . 24  . 19
  . 21  .  .  .  .  . 23  .

SK-17CS-002:
  . 14  .  .  .  .  . 17  .
 16  . 21  .  .  . 28  . 13
  . 22  .  .  .  .  . 29  .
  .  .  .  .  .  .  .  .  .
  .  .  .  . 23  .  .  .  .
  .  .  .  .  .  .  .  .  .
  . 19  .  .  .  .  . 19  .
 17  . 26  .  .  . 29  . 21
  . 21  .  .  .  .  . 24  .

SK-24CS-001:
  . 16  .  .  .  .  . 16  .
 20  . 19  . 23  . 26  .  8
  . 20  .  .  .  .  . 21  .
  .  .  .  . 19  .  .  .  .
  . 19  . 18  . 17  . 18  .
  .  .  .  . 19  .  .  .  .
  . 18  .  .  .  .  . 17  .
 13  . 25  . 21  . 21  . 23
  . 18  .  .  .  .  . 20  .

SK-16CS-006:
  .  .  .  .  .  .  .  .  .
  . 20  . 17  . 27  . 15  .
  .  .  .  .  .  .  .  .  .
  . 14  . 13  . 17  . 16  .
  .  .  .  .  .  .  .  .  .
  . 22  . 29  . 12  . 15  .
  .  .  .  .  .  .  .  .  .
  . 20  . 19  . 11  . 20  .
  .  .  .  .  .  .  .  .  .

SK-16CS-005:
  .  .  .  .  .  .  .  .  .
  . 18  . 17  . 25  . 19  .
  .  .  .  .  .  .  .  .  .
  . 14  . 14  . 21  . 12  .
  .  .  .  .  .  .  .  .  .
  . 23  . 30  . 17  . 11  .
  .  .  .  .  .  .  .  .  .
  . 22  . 14  . 13  . 21  .
  .  .  .  .  .  .  .  .  .

SK-17CS-005:
  3  . 15  .  .  . 16  . 12
  .  .  .  .  .  .  .  .  .
 15  . 27  .  .  . 15  . 20
  .  .  .  .  .  .  .  .  .
  .  .  .  . 23  .  .  .  .
  .  .  .  .  .  .  .  .  .
 11  . 15  .  .  . 28  . 18
  .  .  .  .  .  .  .  .  .
  5  .  6  .  .  . 15  .  6

SK-20CS-002:
  . 13  .  .  .  .  . 16  .
 14  . 19  .  .  . 17  . 19
  . 22  .  .  .  .  . 13  .
  .  .  .  . 19  .  .  .  .
  .  .  . 28  . 21  .  .  .
  .  .  .  . 23  .  .  .  .
  . 23  .  .  .  .  . 21  .
 15  . 18  .  .  . 13  . 11
  . 11  .  .  .  .  .  9  .


Solutions:

Hidden Text: Show

Code: Select all

647958321138642957295731864576184239982367145314529678763815492451293786829476513 # SK-17CS-004
312786945596314782478952631821643597963527418754198326239865174185479263647231859 # SK-17CS-003
352678941198354672467291835723185496684932157915746328239817564571469283846523719 # SK-17CS-002
512738964498516732673294851325481697786952413941367528259843176134679285867125349 # SK-24CS-001
971263854236584791854179623413928576625741938789356412147892365562437189398615247 # SK-16CS-006
974231865213685794865479321541928673326754918789163542457892136632517489198346257 # SK-16CS-005
529687431147523689368941752895172346673459128412836597954718263281364975736295814 # SK-17CS-005
547362189912548367836719254675924813328157946194683572751296438469831725283475691 # SK-20CS-002


[HATMAN]

MM

I fully agree with Tarek - beautiful concept.

When I have solved a few I will create some.

Cheers

Maurice

[HATMAN]

I realised that these are anti-king zero twin killers so I loaded some into JSudoku.
SK-17CS-004 was pleasant to do but it was only at the end with potential multiple solutions that I realised I had missed the Anti-king - JSudoku solves it on singles.
Example 3 unsurprising does not solve also Example 4 does not solve.

I'll try and create one, now

[HATMAN]

SK1

Not too difficult - remember the anti-king

[Mathimagics]

.
Hi Maurice,

That is a perfectly valid puzzle, well done!

You might like to reduce your display size, or even better just show your puzzles as sums, as below. Showing clues in such a big font is not very P & P solver friendly, either, since you leave no room for pencil-marks.

SK-HATMAN-001:

Hidden Text: Show

Code: Select all

 14  . 24  .  .  .  .  . 14
  . 28  .  .  .  .  . 24  .
 19  . 20  . 13  . 20  . 20
  .  .  . 13  . 21  .  .  .
  .  . 13  . 22  . 22  .  .
  .  .  . 22  . 23  .  .  .
  .  . 24  . 22  . 19  .  .
  . 23  .  .  .  .  . 18  .
 10  .  .  .  .  .  .  .  7


[tarek]

My idea about P&P would be a lighter shade of grey solid font or lighter shade of grey outlined font. keeping the font size.

This would allow P&P solvers to write in the cell on the sum number and still not mix them together.

Traditional killer cages will be messy due to the overlap. A smaller font in the corner of the cell is possible but misses the symmetry and strains the eyes.

tarek