The New Sudoku Players' Forum

[Wecoc]

Merry Christmas, guys! (Yes, my timing is as accurate as my hand-made puzzles)

I discovered not so long ago that Snowflake sudoku is a thing.
It's quite a nice variation indeed, kind of similar to the Star sudoku... but not exactly what I had in mind when I first thought about this, so I made it myself.
Each region must contain numbers 1-9. Rows and columns can't have the same number twice EXCEPT in the blue cells.



I made this example manually, it shouldn't be hard to solve.
I'm planning to make another example more challenging but for now I'll keep it simple

[creint]

Solver gives: Multiple solutions

Hidden Text: Show

Code: Select all

Can solve up to this, after this there are multiple solutions.
          .         
  8   . 1 3 . 5   . 
. 1 2 5 . . . 3 . . .
  . 7 3 5 . 8 . 2 1 
  . . 4 7 2 . . . . 
    . . 2 . 3 . 5   
  . 6 . . . . . . . 
  . 8 1 3 7 . 6 4 5 
3 . 5 . . . . 2 3 9 .
  .   . . 5 . .   . 
          .


Atleast 2 solutions:

Code: Select all

          7         
  8   7 1 3 6 5   2 
4 1 2 5 9 4 7 3 6 8 9
  6 7 3 5 9 8 4 2 1 
  5 3 4 7 2 1 8 9 6 
    1 8 2 6 3 9 5   
  9 6 2 4 8 5 7 1 3 
  2 8 1 3 7 9 6 4 5 
3 7 5 6 8 1 4 2 3 9 8
  4   9 6 5 2 1   7 
          4


Code: Select all

          4         
  8   9 1 3 7 5   6 
7 1 2 5 6 9 4 3 7 8 2
  4 7 3 5 6 8 9 2 1 
  5 1 4 7 2 9 8 6 3 
    9 6 2 1 3 4 5   
  3 6 2 8 4 5 1 9 7 
  9 8 1 3 7 2 6 4 5 
3 6 5 7 4 8 1 2 3 9 8
  2   8 9 5 6 7   4 
          1

One with one solution and challenging:

Hidden Text: Show

Code: Select all

          4         
  .   8 . . . .   1 
. 9 . . . 3 . . . . .
  . 5 . . . . . . . 
  . . . . . . 2 . . 
    . 7 . . . . .   
  8 . . . . 1 5 . . 
  . 2 . . 7 . . . 3 
. 6 . . . . . . . . .
  .   . . 9 . 8   7 
          3


[Wecoc]

Solver gives: Multiple solutions

Why this doesn't surprise me?
Well, as I said it was just a fast example I made to test the mechanics involved.

Hidden Text: Show

The solution I found is different, all them seem valid.

Code: Select all

          4         
  8   9 1 3 7 5   2 
7 1 2 5 6 9 4 3 8 7 6
  4 7 3 5 6 8 9 2 1 
  3 1 4 7 2 5 8 9 6 
    9 6 2 1 3 4 5   
  5 6 2 8 4 9 1 7 3 
  9 8 1 3 7 2 6 4 5 
3 6 5 7 4 8 1 2 3 9 8
  2   8 9 5 6 7   4 
          1

At least it doesn't look very hard to adapt the solver this time.

Thanks for testing this, I'll try the one you made.

---

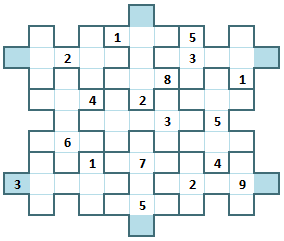
Indexes are assigned without considering the blue cells, since with the white ones you can use r1c1, etc (as always).
The blue cells can be called EXTRA1 or E1 or something like that, I'll name E1 the one in the top, E2 in top-left, E3 in top-right, and so on.

That being said, the white part is almost a full sudoku/jigsaw grid without r1c2, r1c8, r4c1, r4c9, r9c2, r9c8. Adding the blue ones the total of cells is again 81.
This separates the grid between full columns (c3,c4,c5,c6,c7), partial columns (c1,c2,c8,c9), full rows (r2,r3,r4,r6,r7,r8) and partial rows (r1,r5,r9).

Here some observations.

Full and partial rows/columns
All standard jigsaw techniques can be aplied on full rows/columns: Naked pairs, pointing pairs, etc.
Most of them are still valid on partial rows/columns, but you can't use hidden singles since we don't know the row/column has that value or not.

Missing cells
Once the number of candidates not appearing in a partial row or column is the same as the number of cells missing, we can operate the other cells as if it was a full row/column.
That means it can be useful to fill the missing cells with the values they could contain, for example you can fill r5c1 based on c1, but that value can't be used to remove candidates in r5.
In summary, values on a missing cell can be different based on the row or the column, it still makes a valid solution.

Blue cells
Different blue cells can have the same value, even if they are in the same row/column, but that case makes a matching point in the middle of that row/column.
That can help to remove a few candidates, and also means these combinations can't have the same value in any case: E1-E2-E3, E2-E3-E4-E5, E4-E5-E6.