[Sept 5.08]
A Set Logic Solution to Golden Nugget
I have added a set logic solution for Golden Nugget.
See Introduction to Golden Nugget Solution below in this thread or,
SudokuOne WebSite - GN Solution.
The approach is similar to that used on Easter Monster where the set logic can take on most any logical form. Although Golden Nugget is more difficult and lacks the symetery of puzzles like Easter Monster, the set logic solution hints at possible macro structures that might be useful for by hand solutions.
[8-6-08]
Uploaded major revision of SudokuOne WebSite. Major differences are:
. Much shorter, the entire set theory derivation and explanation is now on one page.
. A new section with many simple examples of set theory principles.
. Full attention to previously sketchy areas, i.e., triplets, rank zones, summing of rank effects.
As usual, all feedback is welcome. rab.
[23.5.08]
A Logical Solution to Easter Monster and Sudoku Set Theory
I have added a complete logical solution to Easter Monster to my website, http://sudokuone.com/extra/easter/a_em.htm, and placed a few example eliminations later in this thread. The examples focus on smaller eliminations with interesting logic rather than the large, difficult ones. However, if you need difficulty, see Elimination 8 near the end, which has a rank of 6. For comparison, chains are rank 1 and AALS are rank 2.
A Logical Solution to Top1465 #77 and Sudoku Set Theory
I have found a logical solution to Top1465 #77, which may be of interest, in part because it shows the nature of the logic inside of these monsters. The solution is based on Sudoku Set Theory, which in principle can represent any form of logic including chains. (See, Thread:Local Area Sets and http://sudokuone.com).
I have presented parts of this solution below.
Note: The original version of this puzzle has a hidden single digit 3 in r9c8, which clears the cell and leads to a locked candidates move that clears the digit 4 in r7 of box 7. The solution presented here starts just after these simple moves.
Set Logic Solns: Top1465#77, Easter Mons. Golden Nugget
49 posts
• Page 1 of 4 • 1, 2, 3, 4
Set Logic Solns: Top1465#77, Easter Mons. Golden Nugget
Last edited by Allan Barker on Fri Sep 12, 2008 5:24 pm, edited 10 times in total.
- Allan Barker
- Posts: 266
- Joined: 20 February 2008
A Logical Solution to Top1465 #77, Sudoku Set Theory
Many difficult eliminations that cannot be represented by other methods can be explained relatively easily by set theory principles. Less difficult eliminations produced logic like 3D Kraken fish, nice loops, grouped loops, ALS, etc. Interestingly, there were no long chains and the longest bi-value chain was only about 6 links. Nrct chains are seen since they can represent a much wider variety of logic.
The smallest size logic (found) was used for each step and the solution required 41 eliminations before the first assignment. The puzzle's ferocity diminished somewhat after the first assignment, which was followed by more familiar kinds of logic and a few difficult moves. Some example eliminations are shown below and the complete solution is available at http://sudokuone.com.
Eliminations are written in standard notation except for sets, which are written in a form that makes them easy to recognize. The notation follows the definition of Sudoku sets in 3D, and adds an extra number so that row 4 contains row sets r41 to r49. The extra number is the digit except for cell sets, which are noted by row and column. The four types of sets are then:
row = R(row, digit), column = C(column, digit), cell = N(row, column), box = B(box, digit)
Subgroups like c51, c53, and c59 are written as c5(139). Sorry for any inconvenience. On the otherhand, set theory says that all eliminations can be understood based on sets alone without candidate details. This notation is used with diagrams that provide exct candidate details.
Quick Guide to Sudoku Set Logic
The following is a quick description of how Sudoku set logic can be applied to complex logic however, it is not a complete set guide rules. I hope to have such a set of rules soon.
1. Every solution is based on two groups of sets. The set group exactly contains a group of candidates and the linkset group contains these candidates as well as other candidates that are potential eliminations.
2. The number of linksets minus the number of sets is called rank, which relates to missing constraints. Rank is a distributed property of the logic and applies everywhere within a logical structure except for conditions noted below.
3. Rank 0 eliminates any additional candidates inside of linksets. Common examples include singles, locked candidates, ALCs, X-wing, swordfish, etc.
4. Rank 1 eliminates any additional candidates where two linksets overlap. Many Sudoku methods fall into this category such as finned fish, chains, discontinuous nice loops, etc.
5. Ranks 2 (or 3) logic requires 3 (or 4) simultaneously overlapping linksets to cause eliminations.
6. Ranks higher than 3 can only cause eliminations when combined with triplets, described next.
7. A triplet is a single candidate that connects three sets. A set-triplet has two sets and one linkset, and a linkset-triplet has two linksets and one set. Triplets "point" in the direction of the minor link, i.e., the linkset direction of a two set triplet. The two types of triplets are similar but have different properties.
8. Triplets can divide logic into high rank and low rank regions and therefore change the number of linksets that are needed to eliminate a candidate, but this must follow specific rules. When linkset triplets point in the direction of a candidate, it may reduce the number of linksets required to eliminate the candidate.
9. Set triplets can increase the number of overlap linksets required to make an elimination if they reduce the number of true nodes (assigned candidates) guaranteed to be in the set group. Link-triplets cannot.
10. The candidate in a set-triplet with an unconnected linkset can be assigned in rank 0 logic.
11. When triplets are located and aligned correctly, their effects can be additive however, complex arrangements often require consideration or additional logical analysis.
12. When two blocks of logic are (hypothetically) combined, each retains its original rank internally and the rank of the combined logic is the sum of the individual ranks. Eliminations can occur when linksets of different blocks overlap based on the overall rank and triplets used to link blocks.
Elimination 1
The first elimination uses 8 sets, r46 c5(139) c76 n23 n3(12), connected through 9 linksets, r26 r3(16) c66 n(146)5 b1(45). The extra linkset makes the logic rank 1 thus, two linksets must overlap to eliminate a candidate. The elimination is shown below at the intersection of r1 and c5 at digit level 6. The logic contains two ALS blocks in b1 and in c5 that connect via r31. The candidate sites at the intersection of sets r26 and c56. The elimination is summarized as:
Rank 1: [r46 c5(139) c76 n23 n3(12)] r26*c56 => r2c5 <> 6.
which has the form [ set group ] linkset-overlap => result.
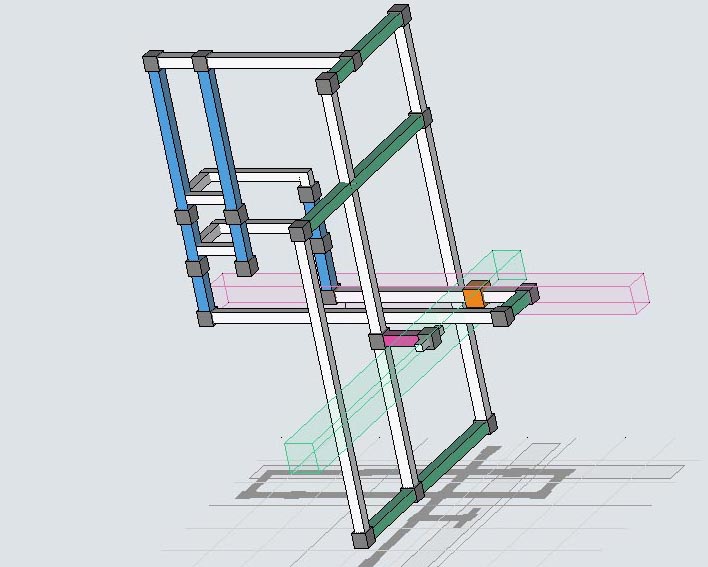
Elimination 12, rank 2
Elimination 12 is large but logically simple. The logic is rank 2 requiring 3 overlap linksets, which might be 4 because the set-triplet S at r1c1(9). Link-triplet V decreases the rank of linkset A which overlaps linkset B. Linket B is located on the minor side of set-triplet S thus the triplet cannot affect the rank. Therefore, r2c1(6) can be eliminated by two overlapping linksets. The logic is summarized below where the V indicates to effect of the link-triplet reducing the overlap linksets.
Rank 2, [r11 r2(19) r32 n35 b19 b3(67) b8(259)](V)r27*n21 => r2c1 <> 6.
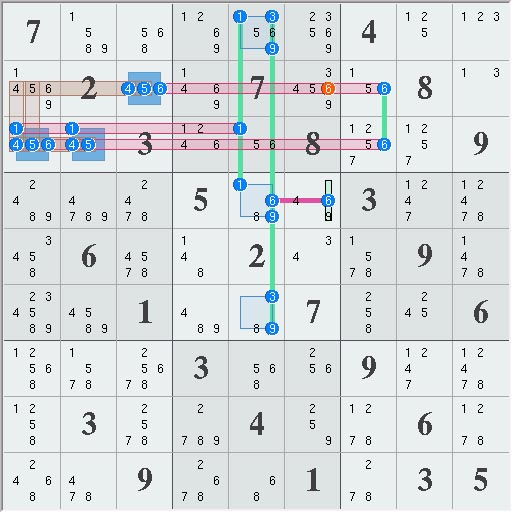
Elimination 16, rank 3
Elimination 16 was one of the larger ones with 18 sets and 43 candidates. With 21 linksets it has a rank of 3, which would require 4 intersecting linksets to eliminate a candidate. Worse, it has multiple set-triplets S that might require additional intersecting linksets. However, digit 5 at r1c2 sits at the intersection of 4 linksets as shown below. Note: this image has been rotated so that row 1 is in the foreground. A study of the set-triplets S shows they can only incresae the rank by 1 and that the 2 link-triplets V near intersecting linkset r15 help to lower the required rank thus r1c2 <> 5.
Rank 3, [r(369)2 r64 r37 c13 c(346)4 c85 c76 n23 n41 n56 n6(25) b19 b35]r15*c25*n12*b15 => r1c2 <> 5.
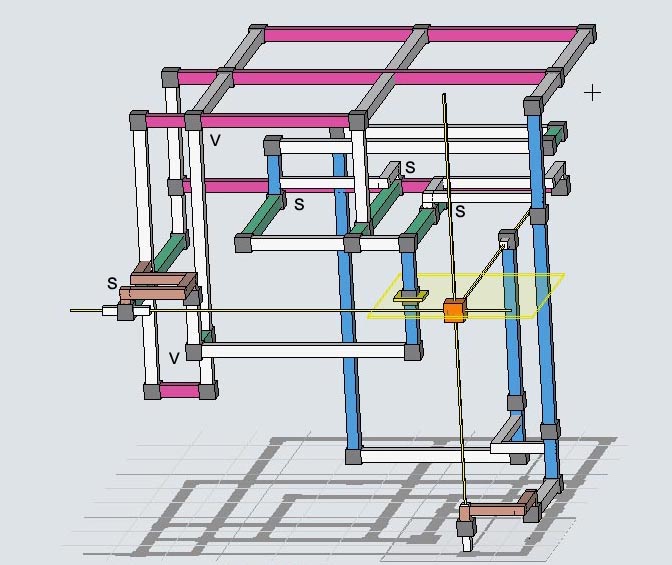
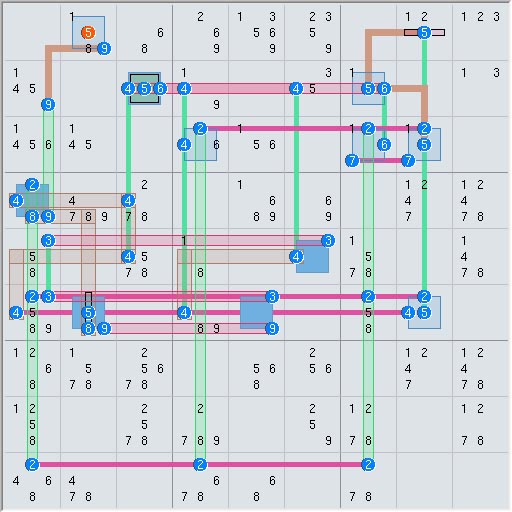
Elimination 20, big head
In elimination 20, set-triplet S seperates two blocks of logic where the link side looks like a big head on a blue pole and the set side makes a red and white "goal post". The logic is rank 2 so 3 linksets must intersect for an elimination however box set B connects to a link-triplet which decreses its rank by one. This box set then intersects the left side of the goal post made of linkset C. The set-triplet S cannot increase the rank of linkset B becasue B is on the minor side of S. The elimination is summarized as:
Rank 2, [r34 r51 r63 c19 c34 c59 c6(34) n19 n2(49) b19 b22](V)n61*b44 => r6c1 <> 4
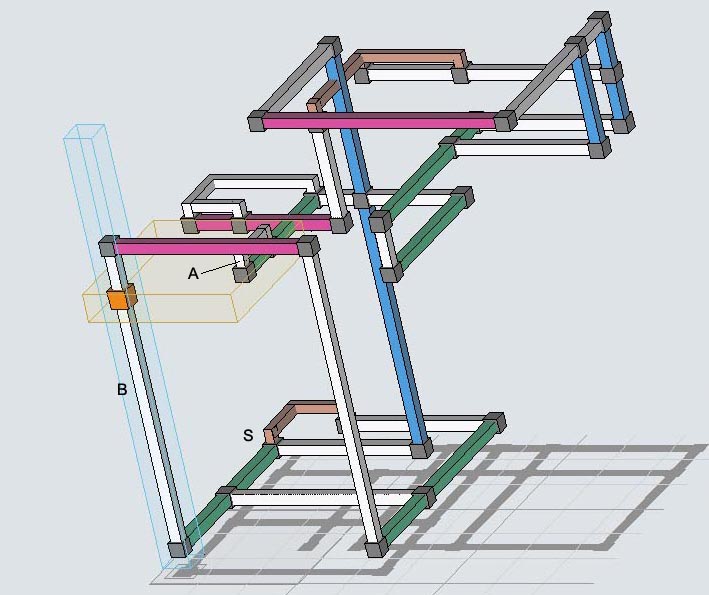
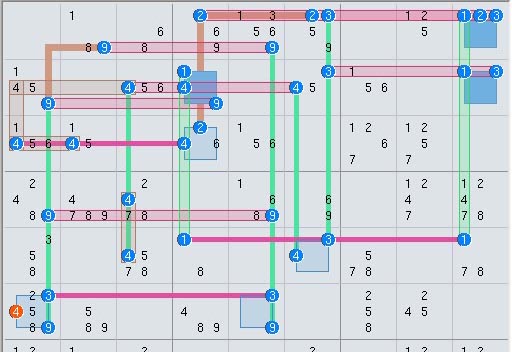
Elimination 4, tough example
This logic has 15 sets, 17 linksets and a rank of 2 therefore 3 intersecting linksets are needed for eliminations. However, the 2 link-triplets pointing to linkset A can raise its rank to 0 and cause eliminations, but only if no set-triplets are occupied. (The black color indicates rank 0). A look at connecting sets shows that when A is not occupied, both link triplets V are occupied and all set-triplets S must be empty, which can be proved given the set-triplets r1c5(9), r1c5(3), r3c5(9) and link-triplets r6c1(3), r4c5(9) and assuming A is empty, r6c5 <> 3 and r6c5 <> 9, then
r6c5<>3 => r6c1=3 ,r1c5=3;
r1c5=3 => r1c5<>1,r1c5<>9;
r6c5<>9, r1c5<>9 => r4c5=9;
r4c5=9 => r3c5<>9;
Thus the set triplets cannot be occupied and the link triplets decrease set A's rank to 0. Therefore r6c5 <> 8, or in short form where the double v indicates the link triplets:
Rank 2, [r1(1689) r21 r46 r53 r63 c19 c5(139) c64 b25 b51](VV)n65 => r6c5 <> 8.
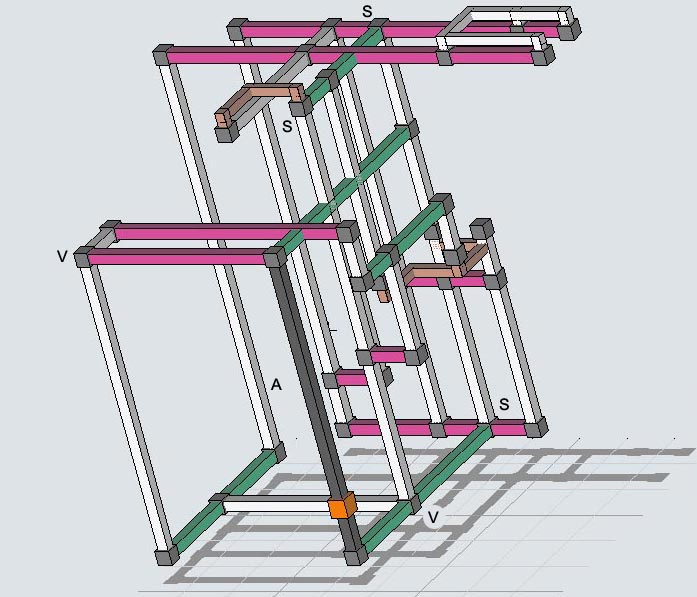
Elimination 57, big 3D Kraken fish
Elimination 57 is an example of the easier logic found after the first assignments. This logic forms a large 3D Kraken fish made of bi-value sets. The set logic is:
Rank 1 [r(47)2 r(28)9 c29 c34 b2(24) b47]c62*n86 => r8c6 <> 2. Big Kraken Fish.
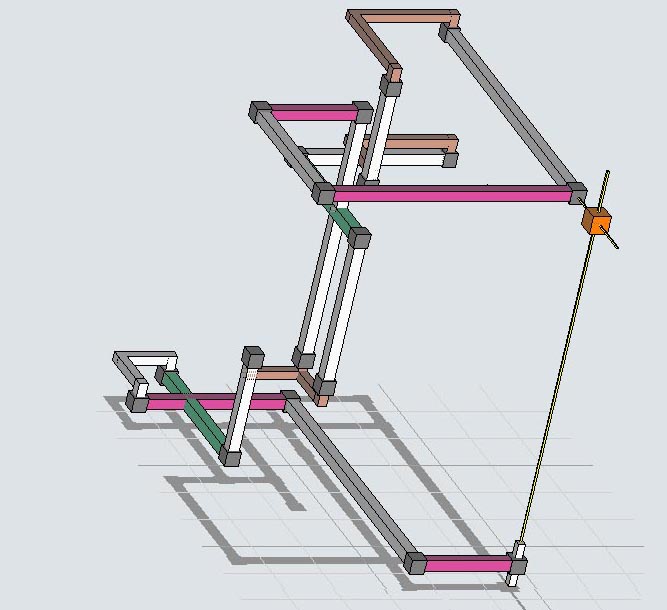
Elimination 55, two loop triplet
Elimination 55 is simple but illustrates triplets. The logic is rank 1 with 7 sets and 8 linksets. It has dual loops that connect to the link-triplet at r1c9n1. The triplet points in the direction of the foreground loop making it rank 0, indicated in black. However, the candidate is just inside the rank 1 loop and is eliminated by the overlap of row set r21 and box set b31, whose elimination zones are highlighted.
Rank 1, [r11 c(156)3 n2(49) b19]r21* b31 => r1c7 <> 1. Grouped Loops
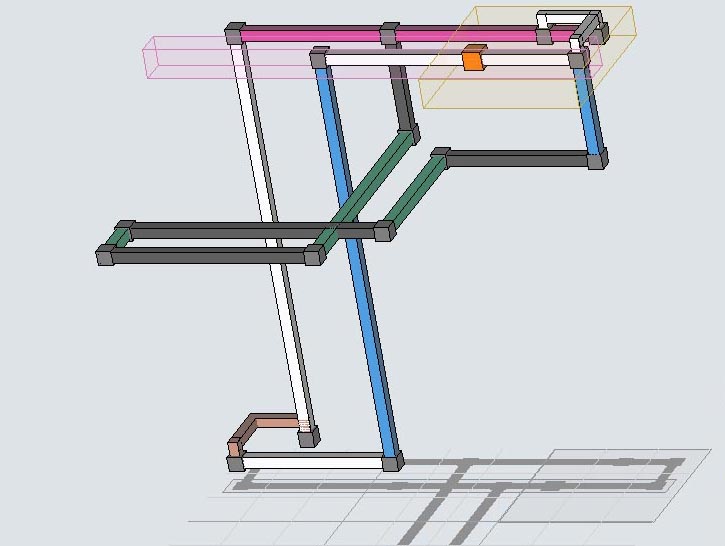
List of Eliminations
The following list contains all eliminations except for those due to singles.
1. R1, 8, [r46 c5(139) c76 n23 n3(12)] r26*c56 => r2c5 <> 6.
2. R4, 10, [r(158)5 c(15)3 c76 n23 n3(125)](ss) r35*b35*c75 => r3c7 <> 5.
3. R2, 12, [r46 r53 c51 c(15)3 c(346)4 n32 n6(245)](s.s) n15*b45 => r5c1 <> 5.
4. R2, 15, [r1(1689) r21 r46 r53 r63 c19 c5(139) c64 b25 b51](vv)n65 => r6c5 <> 8.
5. R3, 14, [r3(24) r9(24) c(46)2 c(25)5 n1(89) n29 n68 n76 b76](s)r64*c24*n62 => r6c2 <> 4.
6. R2, 11, [r16 r25 c85 n35 n6(25) b1(189) b4(35)](v)c35*n13 => r1c3 <> 5.
7. R2, 18, [r2(139) r89 c(578)1 c64 c(27)5 n1(89) n29 n54 n64 b2(25) b85]()n24*b21 => r2c4 <> 1.
8. R3, 15, [r(369)2 r(67)4 c13 c34 c9(27) n48 n56 b24 b4(27) b51](vx)r54*c44*n54 <> r5c4 <> 4.
9. R3, 13, [c65 n3(25) n56 n6(2457) n75 n9(257) b56](vx)n46*b54 => r4c6 <> 4.
10. R1, 4, [r89 c4(67) n46]c66*b26 <> r1c6 <> 6.
11. R4, 17, [r1(68) r53 r6(234) r92 c32 c(36)4 c(125)9 n(23)4 b5(19)](sm)
12. R2, 11, [r11 r2(19) r32 n35 b19 b3(67) b8(259)](v)r27*n21 => r2c1 <> 6.
13. R3, 19, [r16 r2(49) r63 c48 n3(125) n5(16) n6(25) b1(18) b54 b8(2579)](s.sv)r26*b26 => r2c4 <> 6.
14. R4, 14, [r1(68) r5(135) c5(139) c64 n2(3469) b19](svm)c41*n14*b21 => r1c4 <> 1.
15. R1, 17, [r2(59) r5(35) r6(3459) r89 c(36)4 n24 n5(146) n64 b85](v)r75*c15 => r7c1 <> 5.
16. R3, 18, [r(369)2 r64 r37 c13 c(346)4 c85 c76 n23 n41 n56 n6(25) b19 b35](s)r15*c25*n12*b15 => r1c2 <> 5.
17. R2, 9, [r(28)9 c13 c5(35) c85 b(148)5](s)r75*c35 => r7c3 <> 5.
18. R4, 7, [r29 r41 c25 n(69)2 n35 b1(4568) b36 b5(69) b65 b8(579)](v.vs)n57*b61 => r5c7 <> 1.
19. R1, 11, [r51 r63 c(36)4 c19 n24 n42 n5(136) n62](s.s)r54*n59 => r5c9 <> 4.
20. R2, 13, [r34 r51 r63 c19 c34 c59 c6(34) n19 n2(49) b19 b22](s)n61*b44 => r6c1 <> 4.
21. R1, 12, [r23 r51 r64 c53 c(69)4 n1(89) n56 b2(15) b61](ss)c91*n79 => r7c9 <> 1.
22. R2, 13, [r23 r51 r64 c48 c94 n19 n7(56) n95 b5(1369)](vsga)r72*c92*n79 => r7c9 <> 2.
23. R3 14, [r13 r5(47) c(78)1 n2(369) n3(125) b3(567)](vv) c87*n48*b67 => r4c8 <> 7.
24. R3, 16, [r48 r5(18) r6(24) r92 c13 c34 c4(78) n(26)4 n56 b42 b6(57)](svm)n61*b48 => r6c1 <> 8.
25. R0, 19, [r51 r(369)2 r64 r29 c34 c4(18) c9(2478) n24 n41 b24 b5(48) b87](s:s)c49*b59 => r6c4 <> 9.
26. R2, 11, [r54 c34 n(256)4 n65 n56 b1(89) b4(79)](s)c38*n43 => r4c3 <> 8.
27. R3, 15, [r2(15) r55 r6(24) c1(39) c63 n19 n48 n56 n6(247) b51](s.v)c92*b62 => r4c8 <> 2.
28. R1, 2, [r32 c92]r82*c42 => r8c4 <> 2.
29. R1, 11, [r23 r64 c51 c(89)2 c64 n1(89) n29 b25 b61](ss) b32 => r3c7 <> 2.
30. R1, 12, [r3(27) c(3469)2 c(36)4 c(347)6 b24](s)r24 => r2c1 <> 4.
31. R2, 12, [r(3469)2 r(39)7 c3(24) c46 n13 b24 b47]() c38*n53 => r5c3 <> 8.
32. R3, 10, [r32 r5(34) r94 c(34)4 c(28)7 n64 b48](s)c14*n44*b44 => r4c1 <> 4.
33. R3, 15, [r29 r89 r9(246) c(3469)2 c46 c47 c28 n13 n41 b88](vvm)r72,b92 => r7c8 <> 2.
34. R2, 11, [r32 r51 r64 c82 n1(689) n2(49) n56 b61](s.v) c91 => r8c8 <> 1.
35. R3, 14, [r(346)2 r53 r(14)6 r(16)8 c18 c3(48) c44 b54 b86](svm) c46*n34 <> r3c4 <> 6.
36. R0, 5, [r(39)2 c14 n34 b62](s) c42 => r2c4 <> 2.
37. R1, 9, [r(23)6 r78 c87 n13 n37 n95 b9(14)](v) c38*b78 => r8c3 <> 8.
38. R3 ,13, [r6(234) r92 c19 c32 c4(69) n56 b(47)4 b87 b59](v.vv) n61 => r6c1 <> 5.
39. R1, 11, [r11 c(79)2 c(159)3 n2(69) n56 n61 b19](sv) n15*b25 => r1c5 <> 5.
40. R2, 10, [r2(49) c29 c41 n41 n6(15) b44 b5(48)](vm)r48*n42 => r4c2 <> 8.
41. R2, 11, [r(26)9 c63 c(46)4 c(258)5 b2(25) b53](sv) r35 => r3c1 <> 5.
42. R1, 11, [r2(49) r96 c55 c(34)6 n(389)4 n95 b15](q) n76*b86 => r7c5 <> 6.
43. R1, 18, [r29 r46 r53 r64 r8(19) r96 c64 c(18)5 n14 n2(47) n35 n46 b1(56) b25]() r46*n46 => r4c6 = 6, r4c5 <> 6, r4c6 <> 9, r7c6 <> 6.
44. -R0, 1, [b59] = c59 => r1c5 <> 9. Locked Candidate.
45. -R0, 1, [b86] = r96 => r9c1 <> 6.. Locked Candidate.
46. R1, 10, [r2(139) r53 r81 c15 c64 n76 b2(24)](s) c65*n26 => r2c6 <> 5.
47. -R0, 2, [n(25)6] c63 => r1c6 <> 3. naked pair.
48. R1, 4, [r(16)3 c(79)2] r62*n61 => r6c1 <> 2. 1:2 Chain.
49. -R0, 1, [r62] b62 => r4c8 <> 2. Locked Candidate.
50. R0, 2, [n6(15)] r69 => r6c1 <> 9. naked pair.
51. R1, 3, [r54 n6(24)] n53*b45 => r5c3 <> 5. Chain.
52. R1, 4, [r29 c53 n14 n61]r16 *n15 => r1c5 <> 6, Chain.
53. R1, 4, [r29 r53 n26 n61] r24*n24 => r2c4 <> 4. Chain.
54. R0, 2, [r(25)4]L2 [c(36)4] c34 => r4c3 <> 4. X-Wing.
55. R1, 7, [r11 c(156)3 n2(49) b19]r21* b31 => r1c7 <> 1. Grouped loops.
56. R1, 6, [r15 r26 c3(68) n27 n76] r72*n73 => r7c3 <> 2. 3D Kraken Fish.
57. R1, 9 [r(47)2 r(28)9 c29 c34 b2(24) b47]c62*n86 => r8c6 <> 2. Super Big Kraken Fish.
58. R1, 11, [r75 r89 c2(79) c47 c55 c6(29) n(17)6 b25] r1c6 <> 9, r7c2 <> 5. => r8c6 = 9. => r8c4 <> 9, r8c6 <> 5. Multi-loops lead to assignment.
59. R0, 3, [r(258)5] c75 => r6c7 <> 5. Swordfish.
60. R0, 3, [r1(689)] n12 => r1c2 <> 1. Naked Triple.
61. R1, 3, [r81 c(27)1]n87 => r8c7 = 1 => r3c7 <> 1, r7c8 <> 1, r8c1 <> 1, r8c7 <> 2,7,8. Dis. nice loop.
62. R0, 3, [r1(13) n29] b31 => r3c8 <> 1. Almost Locked Candidates.
63. R0, 5, [r26 c87 n(17)3 n37] r77 => r7c1 <> 7, r7c9 <> 7. Grouped Continuous Nice Loop.
64. R1. 7, [r(19)6 c21 c38 n35 n7(25)]r71 => r7c2 = 1, => r3c2 <> 1, r7c1 <> 1, r7 c2 <> 6. Grouped Discontinuous . Nice Loop.
65. R1 , 4 [c44 n32 n6(24)] r64 => r6c4 = 4, => r3c4 <> 4, r6c4 <> 8, r6c8 <> 4, r5c6 <> 4. D. Nice Loop.
Moves 66 to 77 are all singles.
1. R0, 1, [b47] r47 => r4c9 <> 7. Locked Candidates.
2. R0, 2, [n2(37)]r25 => r2c1 <> 5. Naked Pair.
3. R0, 3, [r4(279)]L3 n41 => r4c1 <> 8. Hidden Triple.
4. R1, 5, [r85 n(57)1 n23 b76] c16 => r7c1 = 6, => r7c3 <> 6, r7c1 <> 8, r3c1 <> 6. Dicont. Nice loop.
5. R0, 5, [r49 r94 c27 n(23)1]n92 => r9c2 <> 8. Continuous Nice Loop.
6. R1, 3, [r(167)8]c78*b98 => r9c7 <> 8, r4c9 <> 9, r5c9 <> 8. Discontinuous Nice Loop.
7. -R0, 1 [c78] b68 => r4c9 <> 8, r5c9 <> 8. Locked Candidates.
Remaining eliminations are singles.
Many difficult eliminations that cannot be represented by other methods can be explained relatively easily by set theory principles. Less difficult eliminations produced logic like 3D Kraken fish, nice loops, grouped loops, ALS, etc. Interestingly, there were no long chains and the longest bi-value chain was only about 6 links. Nrct chains are seen since they can represent a much wider variety of logic.
The smallest size logic (found) was used for each step and the solution required 41 eliminations before the first assignment. The puzzle's ferocity diminished somewhat after the first assignment, which was followed by more familiar kinds of logic and a few difficult moves. Some example eliminations are shown below and the complete solution is available at http://sudokuone.com.
Eliminations are written in standard notation except for sets, which are written in a form that makes them easy to recognize. The notation follows the definition of Sudoku sets in 3D, and adds an extra number so that row 4 contains row sets r41 to r49. The extra number is the digit except for cell sets, which are noted by row and column. The four types of sets are then:
row = R(row, digit), column = C(column, digit), cell = N(row, column), box = B(box, digit)
Subgroups like c51, c53, and c59 are written as c5(139). Sorry for any inconvenience. On the otherhand, set theory says that all eliminations can be understood based on sets alone without candidate details. This notation is used with diagrams that provide exct candidate details.
Quick Guide to Sudoku Set Logic
The following is a quick description of how Sudoku set logic can be applied to complex logic however, it is not a complete set guide rules. I hope to have such a set of rules soon.
1. Every solution is based on two groups of sets. The set group exactly contains a group of candidates and the linkset group contains these candidates as well as other candidates that are potential eliminations.
2. The number of linksets minus the number of sets is called rank, which relates to missing constraints. Rank is a distributed property of the logic and applies everywhere within a logical structure except for conditions noted below.
3. Rank 0 eliminates any additional candidates inside of linksets. Common examples include singles, locked candidates, ALCs, X-wing, swordfish, etc.
4. Rank 1 eliminates any additional candidates where two linksets overlap. Many Sudoku methods fall into this category such as finned fish, chains, discontinuous nice loops, etc.
5. Ranks 2 (or 3) logic requires 3 (or 4) simultaneously overlapping linksets to cause eliminations.
6. Ranks higher than 3 can only cause eliminations when combined with triplets, described next.
7. A triplet is a single candidate that connects three sets. A set-triplet has two sets and one linkset, and a linkset-triplet has two linksets and one set. Triplets "point" in the direction of the minor link, i.e., the linkset direction of a two set triplet. The two types of triplets are similar but have different properties.
8. Triplets can divide logic into high rank and low rank regions and therefore change the number of linksets that are needed to eliminate a candidate, but this must follow specific rules. When linkset triplets point in the direction of a candidate, it may reduce the number of linksets required to eliminate the candidate.
9. Set triplets can increase the number of overlap linksets required to make an elimination if they reduce the number of true nodes (assigned candidates) guaranteed to be in the set group. Link-triplets cannot.
10. The candidate in a set-triplet with an unconnected linkset can be assigned in rank 0 logic.
11. When triplets are located and aligned correctly, their effects can be additive however, complex arrangements often require consideration or additional logical analysis.
12. When two blocks of logic are (hypothetically) combined, each retains its original rank internally and the rank of the combined logic is the sum of the individual ranks. Eliminations can occur when linksets of different blocks overlap based on the overall rank and triplets used to link blocks.
Elimination 1
The first elimination uses 8 sets, r46 c5(139) c76 n23 n3(12), connected through 9 linksets, r26 r3(16) c66 n(146)5 b1(45). The extra linkset makes the logic rank 1 thus, two linksets must overlap to eliminate a candidate. The elimination is shown below at the intersection of r1 and c5 at digit level 6. The logic contains two ALS blocks in b1 and in c5 that connect via r31. The candidate sites at the intersection of sets r26 and c56. The elimination is summarized as:
Rank 1: [r46 c5(139) c76 n23 n3(12)] r26*c56 => r2c5 <> 6.
which has the form [ set group ] linkset-overlap => result.


Elimination 12, rank 2
Elimination 12 is large but logically simple. The logic is rank 2 requiring 3 overlap linksets, which might be 4 because the set-triplet S at r1c1(9). Link-triplet V decreases the rank of linkset A which overlaps linkset B. Linket B is located on the minor side of set-triplet S thus the triplet cannot affect the rank. Therefore, r2c1(6) can be eliminated by two overlapping linksets. The logic is summarized below where the V indicates to effect of the link-triplet reducing the overlap linksets.
Rank 2, [r11 r2(19) r32 n35 b19 b3(67) b8(259)](V)r27*n21 => r2c1 <> 6.


Elimination 16, rank 3
Elimination 16 was one of the larger ones with 18 sets and 43 candidates. With 21 linksets it has a rank of 3, which would require 4 intersecting linksets to eliminate a candidate. Worse, it has multiple set-triplets S that might require additional intersecting linksets. However, digit 5 at r1c2 sits at the intersection of 4 linksets as shown below. Note: this image has been rotated so that row 1 is in the foreground. A study of the set-triplets S shows they can only incresae the rank by 1 and that the 2 link-triplets V near intersecting linkset r15 help to lower the required rank thus r1c2 <> 5.
Rank 3, [r(369)2 r64 r37 c13 c(346)4 c85 c76 n23 n41 n56 n6(25) b19 b35]r15*c25*n12*b15 => r1c2 <> 5.


Elimination 20, big head
In elimination 20, set-triplet S seperates two blocks of logic where the link side looks like a big head on a blue pole and the set side makes a red and white "goal post". The logic is rank 2 so 3 linksets must intersect for an elimination however box set B connects to a link-triplet which decreses its rank by one. This box set then intersects the left side of the goal post made of linkset C. The set-triplet S cannot increase the rank of linkset B becasue B is on the minor side of S. The elimination is summarized as:
Rank 2, [r34 r51 r63 c19 c34 c59 c6(34) n19 n2(49) b19 b22](V)n61*b44 => r6c1 <> 4


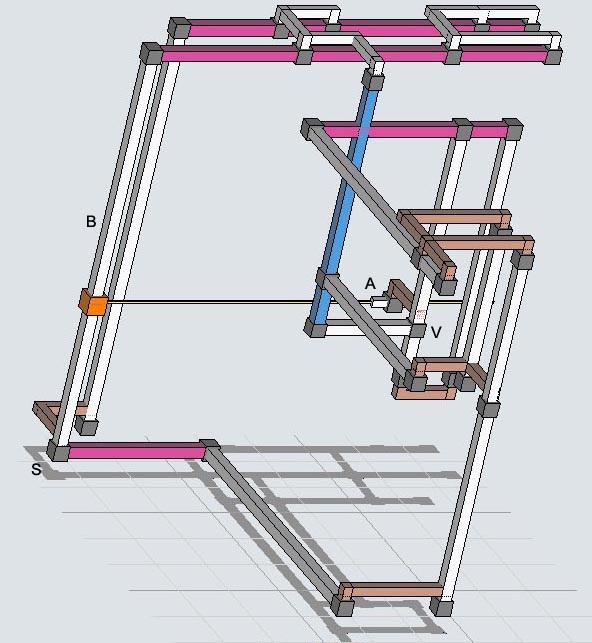
Elimination 4, tough example
This logic has 15 sets, 17 linksets and a rank of 2 therefore 3 intersecting linksets are needed for eliminations. However, the 2 link-triplets pointing to linkset A can raise its rank to 0 and cause eliminations, but only if no set-triplets are occupied. (The black color indicates rank 0). A look at connecting sets shows that when A is not occupied, both link triplets V are occupied and all set-triplets S must be empty, which can be proved given the set-triplets r1c5(9), r1c5(3), r3c5(9) and link-triplets r6c1(3), r4c5(9) and assuming A is empty, r6c5 <> 3 and r6c5 <> 9, then
r6c5<>3 => r6c1=3 ,r1c5=3;
r1c5=3 => r1c5<>1,r1c5<>9;
r6c5<>9, r1c5<>9 => r4c5=9;
r4c5=9 => r3c5<>9;
Thus the set triplets cannot be occupied and the link triplets decrease set A's rank to 0. Therefore r6c5 <> 8, or in short form where the double v indicates the link triplets:
Rank 2, [r1(1689) r21 r46 r53 r63 c19 c5(139) c64 b25 b51](VV)n65 => r6c5 <> 8.


Elimination 57, big 3D Kraken fish
Elimination 57 is an example of the easier logic found after the first assignments. This logic forms a large 3D Kraken fish made of bi-value sets. The set logic is:
Rank 1 [r(47)2 r(28)9 c29 c34 b2(24) b47]c62*n86 => r8c6 <> 2. Big Kraken Fish.

Elimination 55, two loop triplet
Elimination 55 is simple but illustrates triplets. The logic is rank 1 with 7 sets and 8 linksets. It has dual loops that connect to the link-triplet at r1c9n1. The triplet points in the direction of the foreground loop making it rank 0, indicated in black. However, the candidate is just inside the rank 1 loop and is eliminated by the overlap of row set r21 and box set b31, whose elimination zones are highlighted.
Rank 1, [r11 c(156)3 n2(49) b19]r21* b31 => r1c7 <> 1. Grouped Loops

List of Eliminations
The following list contains all eliminations except for those due to singles.
1. R1, 8, [r46 c5(139) c76 n23 n3(12)] r26*c56 => r2c5 <> 6.
2. R4, 10, [r(158)5 c(15)3 c76 n23 n3(125)](ss) r35*b35*c75 => r3c7 <> 5.
3. R2, 12, [r46 r53 c51 c(15)3 c(346)4 n32 n6(245)](s.s) n15*b45 => r5c1 <> 5.
4. R2, 15, [r1(1689) r21 r46 r53 r63 c19 c5(139) c64 b25 b51](vv)n65 => r6c5 <> 8.
5. R3, 14, [r3(24) r9(24) c(46)2 c(25)5 n1(89) n29 n68 n76 b76](s)r64*c24*n62 => r6c2 <> 4.
6. R2, 11, [r16 r25 c85 n35 n6(25) b1(189) b4(35)](v)c35*n13 => r1c3 <> 5.
7. R2, 18, [r2(139) r89 c(578)1 c64 c(27)5 n1(89) n29 n54 n64 b2(25) b85]()n24*b21 => r2c4 <> 1.
8. R3, 15, [r(369)2 r(67)4 c13 c34 c9(27) n48 n56 b24 b4(27) b51](vx)r54*c44*n54 <> r5c4 <> 4.
9. R3, 13, [c65 n3(25) n56 n6(2457) n75 n9(257) b56](vx)n46*b54 => r4c6 <> 4.
10. R1, 4, [r89 c4(67) n46]c66*b26 <> r1c6 <> 6.
11. R4, 17, [r1(68) r53 r6(234) r92 c32 c(36)4 c(125)9 n(23)4 b5(19)](sm)
12. R2, 11, [r11 r2(19) r32 n35 b19 b3(67) b8(259)](v)r27*n21 => r2c1 <> 6.
13. R3, 19, [r16 r2(49) r63 c48 n3(125) n5(16) n6(25) b1(18) b54 b8(2579)](s.sv)r26*b26 => r2c4 <> 6.
14. R4, 14, [r1(68) r5(135) c5(139) c64 n2(3469) b19](svm)c41*n14*b21 => r1c4 <> 1.
15. R1, 17, [r2(59) r5(35) r6(3459) r89 c(36)4 n24 n5(146) n64 b85](v)r75*c15 => r7c1 <> 5.
16. R3, 18, [r(369)2 r64 r37 c13 c(346)4 c85 c76 n23 n41 n56 n6(25) b19 b35](s)r15*c25*n12*b15 => r1c2 <> 5.
17. R2, 9, [r(28)9 c13 c5(35) c85 b(148)5](s)r75*c35 => r7c3 <> 5.
18. R4, 7, [r29 r41 c25 n(69)2 n35 b1(4568) b36 b5(69) b65 b8(579)](v.vs)n57*b61 => r5c7 <> 1.
19. R1, 11, [r51 r63 c(36)4 c19 n24 n42 n5(136) n62](s.s)r54*n59 => r5c9 <> 4.
20. R2, 13, [r34 r51 r63 c19 c34 c59 c6(34) n19 n2(49) b19 b22](s)n61*b44 => r6c1 <> 4.
21. R1, 12, [r23 r51 r64 c53 c(69)4 n1(89) n56 b2(15) b61](ss)c91*n79 => r7c9 <> 1.
22. R2, 13, [r23 r51 r64 c48 c94 n19 n7(56) n95 b5(1369)](vsga)r72*c92*n79 => r7c9 <> 2.
23. R3 14, [r13 r5(47) c(78)1 n2(369) n3(125) b3(567)](vv) c87*n48*b67 => r4c8 <> 7.
24. R3, 16, [r48 r5(18) r6(24) r92 c13 c34 c4(78) n(26)4 n56 b42 b6(57)](svm)n61*b48 => r6c1 <> 8.
25. R0, 19, [r51 r(369)2 r64 r29 c34 c4(18) c9(2478) n24 n41 b24 b5(48) b87](s:s)c49*b59 => r6c4 <> 9.
26. R2, 11, [r54 c34 n(256)4 n65 n56 b1(89) b4(79)](s)c38*n43 => r4c3 <> 8.
27. R3, 15, [r2(15) r55 r6(24) c1(39) c63 n19 n48 n56 n6(247) b51](s.v)c92*b62 => r4c8 <> 2.
28. R1, 2, [r32 c92]r82*c42 => r8c4 <> 2.
29. R1, 11, [r23 r64 c51 c(89)2 c64 n1(89) n29 b25 b61](ss) b32 => r3c7 <> 2.
30. R1, 12, [r3(27) c(3469)2 c(36)4 c(347)6 b24](s)r24 => r2c1 <> 4.
31. R2, 12, [r(3469)2 r(39)7 c3(24) c46 n13 b24 b47]() c38*n53 => r5c3 <> 8.
32. R3, 10, [r32 r5(34) r94 c(34)4 c(28)7 n64 b48](s)c14*n44*b44 => r4c1 <> 4.
33. R3, 15, [r29 r89 r9(246) c(3469)2 c46 c47 c28 n13 n41 b88](vvm)r72,b92 => r7c8 <> 2.
34. R2, 11, [r32 r51 r64 c82 n1(689) n2(49) n56 b61](s.v) c91 => r8c8 <> 1.
35. R3, 14, [r(346)2 r53 r(14)6 r(16)8 c18 c3(48) c44 b54 b86](svm) c46*n34 <> r3c4 <> 6.
36. R0, 5, [r(39)2 c14 n34 b62](s) c42 => r2c4 <> 2.
37. R1, 9, [r(23)6 r78 c87 n13 n37 n95 b9(14)](v) c38*b78 => r8c3 <> 8.
38. R3 ,13, [r6(234) r92 c19 c32 c4(69) n56 b(47)4 b87 b59](v.vv) n61 => r6c1 <> 5.
39. R1, 11, [r11 c(79)2 c(159)3 n2(69) n56 n61 b19](sv) n15*b25 => r1c5 <> 5.
40. R2, 10, [r2(49) c29 c41 n41 n6(15) b44 b5(48)](vm)r48*n42 => r4c2 <> 8.
41. R2, 11, [r(26)9 c63 c(46)4 c(258)5 b2(25) b53](sv) r35 => r3c1 <> 5.
42. R1, 11, [r2(49) r96 c55 c(34)6 n(389)4 n95 b15](q) n76*b86 => r7c5 <> 6.
43. R1, 18, [r29 r46 r53 r64 r8(19) r96 c64 c(18)5 n14 n2(47) n35 n46 b1(56) b25]() r46*n46 => r4c6 = 6, r4c5 <> 6, r4c6 <> 9, r7c6 <> 6.
44. -R0, 1, [b59] = c59 => r1c5 <> 9. Locked Candidate.
45. -R0, 1, [b86] = r96 => r9c1 <> 6.. Locked Candidate.
46. R1, 10, [r2(139) r53 r81 c15 c64 n76 b2(24)](s) c65*n26 => r2c6 <> 5.
47. -R0, 2, [n(25)6] c63 => r1c6 <> 3. naked pair.
48. R1, 4, [r(16)3 c(79)2] r62*n61 => r6c1 <> 2. 1:2 Chain.
49. -R0, 1, [r62] b62 => r4c8 <> 2. Locked Candidate.
50. R0, 2, [n6(15)] r69 => r6c1 <> 9. naked pair.
51. R1, 3, [r54 n6(24)] n53*b45 => r5c3 <> 5. Chain.
52. R1, 4, [r29 c53 n14 n61]r16 *n15 => r1c5 <> 6, Chain.
53. R1, 4, [r29 r53 n26 n61] r24*n24 => r2c4 <> 4. Chain.
54. R0, 2, [r(25)4]L2 [c(36)4] c34 => r4c3 <> 4. X-Wing.
55. R1, 7, [r11 c(156)3 n2(49) b19]r21* b31 => r1c7 <> 1. Grouped loops.
56. R1, 6, [r15 r26 c3(68) n27 n76] r72*n73 => r7c3 <> 2. 3D Kraken Fish.
57. R1, 9 [r(47)2 r(28)9 c29 c34 b2(24) b47]c62*n86 => r8c6 <> 2. Super Big Kraken Fish.
58. R1, 11, [r75 r89 c2(79) c47 c55 c6(29) n(17)6 b25] r1c6 <> 9, r7c2 <> 5. => r8c6 = 9. => r8c4 <> 9, r8c6 <> 5. Multi-loops lead to assignment.
59. R0, 3, [r(258)5] c75 => r6c7 <> 5. Swordfish.
60. R0, 3, [r1(689)] n12 => r1c2 <> 1. Naked Triple.
61. R1, 3, [r81 c(27)1]n87 => r8c7 = 1 => r3c7 <> 1, r7c8 <> 1, r8c1 <> 1, r8c7 <> 2,7,8. Dis. nice loop.
62. R0, 3, [r1(13) n29] b31 => r3c8 <> 1. Almost Locked Candidates.
63. R0, 5, [r26 c87 n(17)3 n37] r77 => r7c1 <> 7, r7c9 <> 7. Grouped Continuous Nice Loop.
64. R1. 7, [r(19)6 c21 c38 n35 n7(25)]r71 => r7c2 = 1, => r3c2 <> 1, r7c1 <> 1, r7 c2 <> 6. Grouped Discontinuous . Nice Loop.
65. R1 , 4 [c44 n32 n6(24)] r64 => r6c4 = 4, => r3c4 <> 4, r6c4 <> 8, r6c8 <> 4, r5c6 <> 4. D. Nice Loop.
Moves 66 to 77 are all singles.
1. R0, 1, [b47] r47 => r4c9 <> 7. Locked Candidates.
2. R0, 2, [n2(37)]r25 => r2c1 <> 5. Naked Pair.
3. R0, 3, [r4(279)]L3 n41 => r4c1 <> 8. Hidden Triple.
4. R1, 5, [r85 n(57)1 n23 b76] c16 => r7c1 = 6, => r7c3 <> 6, r7c1 <> 8, r3c1 <> 6. Dicont. Nice loop.
5. R0, 5, [r49 r94 c27 n(23)1]n92 => r9c2 <> 8. Continuous Nice Loop.
6. R1, 3, [r(167)8]c78*b98 => r9c7 <> 8, r4c9 <> 9, r5c9 <> 8. Discontinuous Nice Loop.
7. -R0, 1 [c78] b68 => r4c9 <> 8, r5c9 <> 8. Locked Candidates.
Remaining eliminations are singles.
Last edited by Allan Barker on Sun May 25, 2008 9:55 am, edited 2 times in total.
- Allan Barker
- Posts: 266
- Joined: 20 February 2008
impressive graphs !!!
regarding the puzzle itself (just to make sure you've got the correct puzzle):
Vidarino's Monster #3
#77 of the top 1465 (WAS the toughest known)
regarding the puzzle itself (just to make sure you've got the correct puzzle):
Vidarino's Monster #3
- Code: Select all
+-------+-------+-------+
| 5 . . | 8 . . | 4 . . |
| . 8 . | . 9 . | . 5 . |
| . . 7 | . . 6 | . . 2 |
+-------+-------+-------+
| . . 4 | . . 3 | . . 6 |
| . 3 . | . . . | . . . |
| 9 . . | 1 . . | . . . |
+-------+-------+-------+
| . . . | 7 . . | 8 . . |
| . 4 . | . 5 . | . 1 . |
| . . 2 | . . 1 | . . 4 |
+-------+-------+-------+
#77 of the top 1465 (WAS the toughest known)
- Code: Select all
+-------+-------+-------+
| 7 . . | . . . | 4 . . |
| . 2 . | . 7 . | . 8 . |
| . . 3 | . . 8 | . . 9 |
+-------+-------+-------+
| . . . | 5 . . | 3 . . |
| . 6 . | . 2 . | . 9 . |
| . . 1 | . . 7 | . . 6 |
+-------+-------+-------+
| . . . | 3 . . | 9 . . |
| . 3 . | . 4 . | . 6 . |
| . . 9 | . . 1 | . . 5 |
+-------+-------+-------+
-

tarek - Posts: 3762
- Joined: 05 January 2006
Tarek,
Oops, thanks. This is the second of the two puzzles, Top1465 #77, once upon a time toughest. Seems I had the two names confused thinking they both referred to the same puzzle.
Oops, thanks. This is the second of the two puzzles, Top1465 #77, once upon a time toughest. Seems I had the two names confused thinking they both referred to the same puzzle.
- Allan Barker
- Posts: 266
- Joined: 20 February 2008
Hi,
I know for long that top1465 #77 is solved easily by my solver, but I never had a look on it.
Some statistical figures:
Solved in 7 seconds. (Golden Nugget same conditions 85 seconds)
31 AICs nets before finding the second fix
11 more to find four more digits.
It’s not so far from what Alan said, but significantly shorter.
Vidarino’s Monster is much easier.
I know for long that top1465 #77 is solved easily by my solver, but I never had a look on it.
Some statistical figures:
Solved in 7 seconds. (Golden Nugget same conditions 85 seconds)
31 AICs nets before finding the second fix
11 more to find four more digits.
It’s not so far from what Alan said, but significantly shorter.
Vidarino’s Monster is much easier.
- champagne
- 2017 Supporter
- Posts: 7831
- Joined: 02 August 2007
- Location: France Brittany
Champange,
I can also see the second assignment after about 30 moves as well, but not much below 30, just depends on starting conditions. What is interesting is the solution profiles are similar, something like Easter Monster looks very different. It makes me wonder what your AIC nets look like. If you can give me a couple of big ones, I can try to plot them with my software.
Am not really working on a solver, per se, (well, of course I am, but in a round about way). What I am trying to do is answer a few questions such as: 1) what does the logic inside a puzzle look like if we make no assumptions on what the solution should be? or 2) what kind of rules can be applied to this "natural logic"? Which is why I found the above solution interesting.
I can also see the second assignment after about 30 moves as well, but not much below 30, just depends on starting conditions. What is interesting is the solution profiles are similar, something like Easter Monster looks very different. It makes me wonder what your AIC nets look like. If you can give me a couple of big ones, I can try to plot them with my software.
Am not really working on a solver, per se, (well, of course I am, but in a round about way). What I am trying to do is answer a few questions such as: 1) what does the logic inside a puzzle look like if we make no assumptions on what the solution should be? or 2) what kind of rules can be applied to this "natural logic"? Which is why I found the above solution interesting.
- Allan Barker
- Posts: 266
- Joined: 20 February 2008
Allan wrote
I anticipated your request, so I am putting the solution on my website.
The permanent entry will be here
http://pagesperso-orange.fr/gpenet/UX/UX.htm
but you have a direct access here
http://pagesperso-orange.fr/gpenet/UX/UX_fichiers/t1465_77_01.htm
the printing rules are here
http://pagesperso-orange.fr/gpenet/UX/UX_fichiers/UXWR.htm
I did not work on that puzzle, so what you have is just a cleaning of the print of my solver.
I hope it will help you.
Missing clearings are coming. As you will see, the cracking is a succession of AIC’s nets.
In that puzzle, AIC’s are most often using strong an weak links coming out of ALS AHS/ACs.
If you have any specific question, I will answer ASAP
It makes me wonder what your AIC nets look like. If you can give me a couple of big ones, I can try to plot them with my software.
I anticipated your request, so I am putting the solution on my website.
The permanent entry will be here
http://pagesperso-orange.fr/gpenet/UX/UX.htm
but you have a direct access here
http://pagesperso-orange.fr/gpenet/UX/UX_fichiers/t1465_77_01.htm
the printing rules are here
http://pagesperso-orange.fr/gpenet/UX/UX_fichiers/UXWR.htm
I did not work on that puzzle, so what you have is just a cleaning of the print of my solver.
I hope it will help you.
Missing clearings are coming. As you will see, the cracking is a succession of AIC’s nets.
In that puzzle, AIC’s are most often using strong an weak links coming out of ALS AHS/ACs.
If you have any specific question, I will answer ASAP
- champagne
- 2017 Supporter
- Posts: 7831
- Joined: 02 August 2007
- Location: France Brittany
how come my puzzle isn't on that list.?
its a cusin to mb-metcalfs it has an er of 11.4
its a cusin to mb-metcalfs it has an er of 11.4
- Code: Select all
*-----------*
|5..|...|..9|
|.2.|1..|.7.|
|..8|...|3..|
|---+---+---|
|.4.|..2|...|
|...|.5.|...|
|...|7.6|.1.|
|---+---+---|
|..3|...|8..|
|.6.|..4|.2.|
|9..|...|..5|
*-----------*
Some do, some teach, the rest look it up.
stormdoku
stormdoku
-

StrmCkr - Posts: 1488
- Joined: 05 September 2006
strmckr wrote
This is a thread open for t1465_77, so I guess your question is wider.
It should come in the thread of hardest puzzles.
I can nevertheless give you some clues.
1) Your puzzle is number 2 in JPF list of hardest puzzles
2) In Gsf list, it has a ranking relatively low ~17000
3)This puzzle has the SK loop. As all puzzles having the same pattern, I think ER is over rating it .
4)Results on my side are very similar to Easter Monster.
solved in 13 seconds
print size of about 200K
to compare to Golden Nugget 85 seconds an about 500K printfile
It is for sure tougher than 1465_77,and clearly in the family of hardest.
how come my puzzle isn't on that list.?
its a cusin to mb-metcalfs it has an er of 11.4
This is a thread open for t1465_77, so I guess your question is wider.
It should come in the thread of hardest puzzles.
I can nevertheless give you some clues.
1) Your puzzle is number 2 in JPF list of hardest puzzles
2) In Gsf list, it has a ranking relatively low ~17000
3)This puzzle has the SK loop. As all puzzles having the same pattern, I think ER is over rating it .
4)Results on my side are very similar to Easter Monster.
solved in 13 seconds
print size of about 200K
to compare to Golden Nugget 85 seconds an about 500K printfile
It is for sure tougher than 1465_77,and clearly in the family of hardest.
- champagne
- 2017 Supporter
- Posts: 7831
- Joined: 02 August 2007
- Location: France Brittany
StrmCkr wrote:how come my puzzle isn't on that list?
What list? If you're referring to the top1465, that's an old list ... and there's no obligation by anyone to keep it current.
AFAIK the most recent comprehensive list of "toughies" is gsf's "q1-taxonomy". Your puzzle is there.
- ronk
- 2012 Supporter
- Posts: 4764
- Joined: 02 November 2005
- Location: Southeastern USA
Hi Allan,
I've been away for some time and I just discover this thread.
Great thing that you could solve this puzzle with your second order resolution rules.
I think you should give the full resolution path (not skip the Singles - except the final ones), so that we can easily see the main steps.
Do you skip only the Singles, as you say, or also other rules? In particular, do you skip the elementary interaction rules?
Why am I askig this? Merely because my resolution path starts with:
At this point, I run out of memory. This is one of the puzzles that are complex not because they don't have enough chains (as EasterMonster) but because they have too many and it is difficult to find the useful ones.
Anyway, before any 2nd order rule is applied, some eliminations are available.
This leads me to the question: do you have any fixed ordering of your rules? What's the part of the rank in it?
I've been away for some time and I just discover this thread.
Great thing that you could solve this puzzle with your second order resolution rules.
I think you should give the full resolution path (not skip the Singles - except the final ones), so that we can easily see the main steps.
Do you skip only the Singles, as you say, or also other rules? In particular, do you skip the elementary interaction rules?
Why am I askig this? Merely because my resolution path starts with:
- Code: Select all
hidden-single-in-a-row ==> r9c8 = 3
row r9 interaction-with-block b7 ==> r7c3 <> 4, r7c2 <> 4, r7c1 <> 4
nrczt9-lr-lasso n6{r1c4 r9c4} - {n6 n8}r9c5 - {n8 n5}r7c5 - {n5 n1}r3c5 - n6{r3c5 r4c5} - n6{r1c5 r1c3} - n8{r1c3 r1c2} - n9{r1c2 r2c1} - n1{r2c1 r1c2} ==> r2c6 <> 6
nrczt11-lr-lasso n4{r4c3 r2c3} - n4{r2c6 r4c6} - n6{r4c6 r4c5} - {n6 n8}r9c5 - {n8 n5}r7c5 - {n5 n1}r3c5 - n1{r1c4 r5c4} - n8{r5c4 r6c4} - n9{r6c4 r6c5} - {n9 n5}r6c2 - {n5 n1}r3c2 ==> r5c1 <> 4
nrczt12-lr-lasso {n8 n6}r9c5 - {n6 n5}r7c5 - {n5 n1}r3c5 - {n1 n9}r4c5 - {n9 n4}r6c4 - {n4 n3}r5c6 - n3{r6c5 r6c1} - n9{r6c1 r2c1} - {n9 n6}r2c4 - n6{r1c4 r1c3} - n8{r1c3 r1c2} - n1{r1c2 r2c1} ==> r6c5 <> 8
nrczt15-lr-lasso {n4 n3}r5c6 - n3{r5c1 r6c1} - {n3 n9}r6c5 - {n9 n6}r4c6 - n4{r4c6 r2c6} - n4{r2c3 r4c3} - n4{r4c8 r6c8} - n2{r6c8 r6c7} - n2{r4c8 r4c1} - n2{r9c1 r9c4} - n2{r1c4 r1c6} - n3{r1c6 r1c5} - {n3 n1}r1c9 - n1{r5c9 r5c7} - n5{r5c7 r6c7} ==> r5c4 <> 4
nrczt15-lr-lasso n6{r2c7 r3c7} - n7{r3c7 r3c8} - n2{r3c8 r3c4} - n4{r3c4 r6c4} - {n4 n3}r5c6 - {n3 n9}r6c5 - {n9 n6}r4c6 - n6{r1c6 r1c3} - n8{r1c3 r1c2} - {n8 n5}r6c2 - {n5 n8}r5c1 - {n8 n1}r5c4 - {n1 n9}r1c4 - {n9 n5}r1c6 - n5{r1c8 r3c8} ==> r2c4 <> 6
At this point, I run out of memory. This is one of the puzzles that are complex not because they don't have enough chains (as EasterMonster) but because they have too many and it is difficult to find the useful ones.
Anyway, before any 2nd order rule is applied, some eliminations are available.
This leads me to the question: do you have any fixed ordering of your rules? What's the part of the rank in it?
- denis_berthier
- 2010 Supporter
- Posts: 4645
- Joined: 19 June 2007
- Location: Paris
Denis,
I too have been away a bit, but I got some work done which I will post soon.
I see why you ask this, my versions of Top1468#77 already include the first two simple moves though I'm aware the original has the single 3 in r9c8. I put a statement to that effect at the top of the thread.
I have two solvers, the first is similar to other solvers and searches based on increasing length (of sets). This solver finds everything. I can then apply restrictions to find what I want, to limit the search, or I can leave the search wide open to study the logic. Restrictions include rank, number of candidates/set, single digit, etc. For instance, I can search for all 3D chains with only bi-value and (hinge like) links. I can also choose the rank along the solution path, which is vaguely similar to selecting things like ALS. This is all easy to say but I often struggle with the implementation.
This solver goes only so far before running out of memory or time (time=memory) like any other. The second solver works on all the same principles except how it finds things. The idea is to treat a solution as a linearly connected group of sets rather than the massively interconnected maze we see in 3 spatial dimensions. This makes it easier to minimize the astromonical combinorics, but not bypass them. This solver finds the same solutions available in the grid as the first solver, but without the fine control on length.
I hope to write all this up and put in on my website sometime. If I get feedback that something is of particular interest, I will try to get that done first.
Now I'm wondering, what is a best solution? The fewest sets or the fewest candidates, or even the easiest (fastest) solution? Nrctz chains and other techniques must have the same issues. I'm beginning to favor the solution that is easiest to understand or the most elegant.
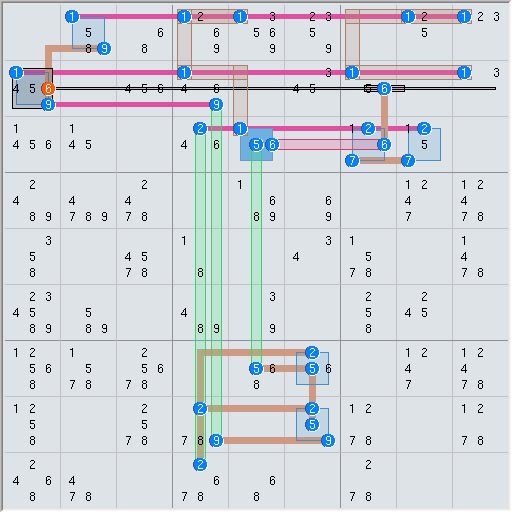
BTW. I took your elimination above and entered it into my solver by placing a set for each of your nine {....} terms and the solver completed the logic producing the elimination shown below. It also decided it did not need a set for n6{r3c5 r4c5}, only the nodes. This 16 set solution is not unlike mine and is even more similar to others I have seen.
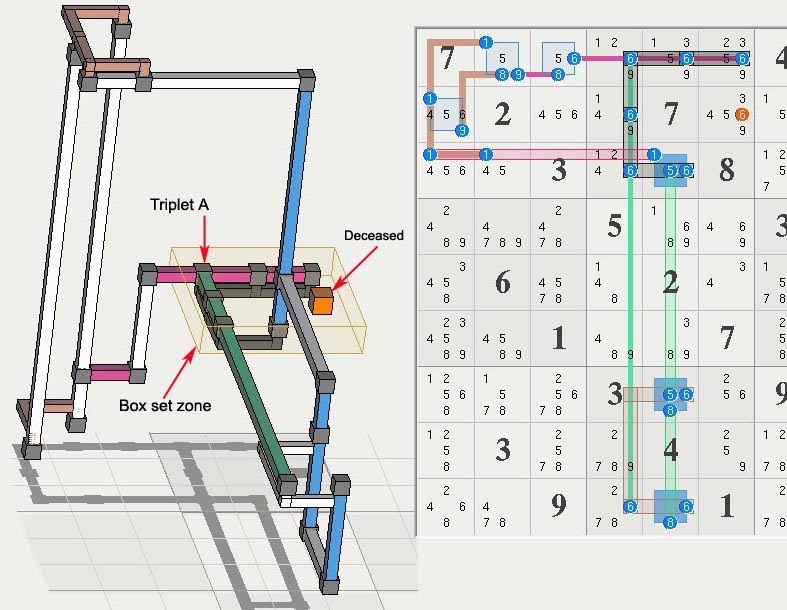
The set logic analysis is: Step 1) 8 sets and 8 linksets means that 8 <true> candidates must be in the 8 linksets (rank 0) thus all 8 linksets can be cleared. Step 2) the triplet A where 2 sets overlap reduces the assured <true> candidates to 7 (rank is now 1) for the whole structure. Step 3) the minor side (box side) of the triplet has a lower rank by one (rule), thus the box set is rank 0 (emphasized in black) and clears the orange candidate.
I too have been away a bit, but I got some work done which I will post soon.
I think you should give the full resolution path ...... Do you skip only the Singles, as you say, or also other rules? In particular, do you skip the elementary interaction rules?
I see why you ask this, my versions of Top1468#77 already include the first two simple moves though I'm aware the original has the single 3 in r9c8. I put a statement to that effect at the top of the thread.
This leads me to the question: do you have any fixed ordering of your rules? What's the part of the rank in it?
I have two solvers, the first is similar to other solvers and searches based on increasing length (of sets). This solver finds everything. I can then apply restrictions to find what I want, to limit the search, or I can leave the search wide open to study the logic. Restrictions include rank, number of candidates/set, single digit, etc. For instance, I can search for all 3D chains with only bi-value and (hinge like) links. I can also choose the rank along the solution path, which is vaguely similar to selecting things like ALS. This is all easy to say but I often struggle with the implementation.
This solver goes only so far before running out of memory or time (time=memory) like any other. The second solver works on all the same principles except how it finds things. The idea is to treat a solution as a linearly connected group of sets rather than the massively interconnected maze we see in 3 spatial dimensions. This makes it easier to minimize the astromonical combinorics, but not bypass them. This solver finds the same solutions available in the grid as the first solver, but without the fine control on length.
I hope to write all this up and put in on my website sometime. If I get feedback that something is of particular interest, I will try to get that done first.
Now I'm wondering, what is a best solution? The fewest sets or the fewest candidates, or even the easiest (fastest) solution? Nrctz chains and other techniques must have the same issues. I'm beginning to favor the solution that is easiest to understand or the most elegant.
nrczt9-lr-lasso n6{r1c4 r9c4} - {n6 n8}r9c5 - {n8 n5}r7c5 - {n5 n1}r3c5 - n6{r3c5 r4c5} - n6{r1c5 r1c3} - n8{r1c3 r1c2} - n9{r1c2 r2c1} - n1{r2c1 r1c2} ==> r2c6 <> 6
BTW. I took your elimination above and entered it into my solver by placing a set for each of your nine {....} terms and the solver completed the logic producing the elimination shown below. It also decided it did not need a set for n6{r3c5 r4c5}, only the nodes. This 16 set solution is not unlike mine and is even more similar to others I have seen.
The set logic analysis is: Step 1) 8 sets and 8 linksets means that 8 <true> candidates must be in the 8 linksets (rank 0) thus all 8 linksets can be cleared. Step 2) the triplet A where 2 sets overlap reduces the assured <true> candidates to 7 (rank is now 1) for the whole structure. Step 3) the minor side (box side) of the triplet has a lower rank by one (rule), thus the box set is rank 0 (emphasized in black) and clears the orange candidate.

- Allan Barker
- Posts: 266
- Joined: 20 February 2008
Hi Allan,
As I understand it, all the potential eliminations are (conceptually) computed in parallel before you make any real elimination. After that, you choose a linear resolution path. => 2 questions.
1) Once an elimination has been made, this changes the sets and linksets for further potential eliminations identified in the first step. Are such changes propagated in the justifications of the further eliminations?
In SudoRules, I avoid "ghosts". All eliminations that'd be justified by candidates already eliminated are discarded. I've proven that there is always a simpler rule that still applies to justify these eliminations. This is intimately related to the confluence property of my theories. I think you have the same with yours.
This mechanism is responsible for some inefficiencies but I wouldn't consider changing it.
2) Once an elimination has been made, this produces new sets and linksets for additional potential eliminations not available in the first step (which may be simpler than those already available). Do you restart the first step after each elimination?
In SudoRules I do (indeed the underlying inference engine does it automatically and incrementally), thus guaranteeing that the logically simpler choice is made at each step.
I don't think one can give an a priori answer to such questions.
(e.g. easiest or fastest for whom: a human or a computer? most elegant wrt to which criteria?)
Yes, of course. Things are nevertheless simpler for nrczt-chains, as there is only one parameter: length. Moreover, I've shown that, statistically, the number of partial chains increases exponentially with the length, so that this parameter, which I chose a priori, is justified a posteriori on a statistical basis.
Things get more complex if I consider all the subtypes of nrczt-chains (nrc, nrct, xy, xyt, hxy,...) and I want to include them in the nrczt ordering.
In my book, I've considered a partial order that is the direct product of two orders:
- length
- xy = hxy < xyt = hxyt < xyzt = hxyzt < nrc < nrct < nrczt
This is justified because finding an xy10 maybe simpler than finding an nrczt7.
In SudoRules, this is implemented with a 3"D-penalty" parameter.
But, in practice, I always set this parameter to 0.
If, instead of nrczt-chains, one considers the usual AICs with ALSs (which have roughly the same resolution power as nrczt), things are more complex from the beginning, because there are two parameters: length of the chains and maximum size of the ALSs. I'd like to make the same statistical computations as I've done for nrczt, but as ALSs are not implemented in SudoRules, I can't. It seems no existing solver can do such computations.
This case seems closer to yours. But you have one more parameter: rank. Could your solver analyse large collections of puzzles and compute the mean number of patterns necessary to find a solution, for each choice of the parameters {rank, max size of the sets, nb of candidates,...}?
The linkset are added automatically?
Does this mean anything special??
Allan Barker wrote:I have two solvers, the first is similar to other solvers and searches based on increasing length (of sets). This solver finds everything. I can then apply restrictions to find what I want, to limit the search, or I can leave the search wide open to study the logic. Restrictions include rank, number of candidates/set, single digit, etc. For instance, I can search for all 3D chains with only bi-value and (hinge like) links. I can also choose the rank along the solution path, which is vaguely similar to selecting things like ALS. This is all easy to say but I often struggle with the implementation.
As I understand it, all the potential eliminations are (conceptually) computed in parallel before you make any real elimination. After that, you choose a linear resolution path. => 2 questions.
1) Once an elimination has been made, this changes the sets and linksets for further potential eliminations identified in the first step. Are such changes propagated in the justifications of the further eliminations?
In SudoRules, I avoid "ghosts". All eliminations that'd be justified by candidates already eliminated are discarded. I've proven that there is always a simpler rule that still applies to justify these eliminations. This is intimately related to the confluence property of my theories. I think you have the same with yours.
This mechanism is responsible for some inefficiencies but I wouldn't consider changing it.
2) Once an elimination has been made, this produces new sets and linksets for additional potential eliminations not available in the first step (which may be simpler than those already available). Do you restart the first step after each elimination?
In SudoRules I do (indeed the underlying inference engine does it automatically and incrementally), thus guaranteeing that the logically simpler choice is made at each step.
Allan Barker wrote:Now I'm wondering, what is a best solution? The fewest sets or the fewest candidates, or even the easiest (fastest) solution?
I'm beginning to favor the solution that is easiest to understand or the most elegant.
I don't think one can give an a priori answer to such questions.
(e.g. easiest or fastest for whom: a human or a computer? most elegant wrt to which criteria?)
Allan Barker wrote:Nrctz chains and other techniques must have the same issues.
Yes, of course. Things are nevertheless simpler for nrczt-chains, as there is only one parameter: length. Moreover, I've shown that, statistically, the number of partial chains increases exponentially with the length, so that this parameter, which I chose a priori, is justified a posteriori on a statistical basis.
Things get more complex if I consider all the subtypes of nrczt-chains (nrc, nrct, xy, xyt, hxy,...) and I want to include them in the nrczt ordering.
In my book, I've considered a partial order that is the direct product of two orders:
- length
- xy = hxy < xyt = hxyt < xyzt = hxyzt < nrc < nrct < nrczt
This is justified because finding an xy10 maybe simpler than finding an nrczt7.
In SudoRules, this is implemented with a 3"D-penalty" parameter.
But, in practice, I always set this parameter to 0.
If, instead of nrczt-chains, one considers the usual AICs with ALSs (which have roughly the same resolution power as nrczt), things are more complex from the beginning, because there are two parameters: length of the chains and maximum size of the ALSs. I'd like to make the same statistical computations as I've done for nrczt, but as ALSs are not implemented in SudoRules, I can't. It seems no existing solver can do such computations.
This case seems closer to yours. But you have one more parameter: rank. Could your solver analyse large collections of puzzles and compute the mean number of patterns necessary to find a solution, for each choice of the parameters {rank, max size of the sets, nb of candidates,...}?
Allan Barker wrote:I took your elimination above and entered it into my solver by placing a set for each of your nine {....} terms and the solver completed the logic producing the elimination shown below.
The linkset are added automatically?
Allan Barker wrote:It also decided it did not need a set for n6{r3c5 r4c5}, only the nodes.
Does this mean anything special??
- denis_berthier
- 2010 Supporter
- Posts: 4645
- Joined: 19 June 2007
- Location: Paris
Denis, some quick answers.
Yes, they are, meaning I start from scratch for the next elimination.
I have always assumed this to be the case, without proof, i.e., that an elimination can open new opportunities to eliminate other candidates that could not be cleared before, or in your words, open shorter paths. (I now see that these are almost your exact words below). Further, doesn't this imply that given a group of candidates that cause an elimination, if one or more of the candidates is removed then the remaining candidates (alone) will still cause the same elimination?
Yes.
Yes, in principle solver 1 can do that kind of stastical work, but I have not configured it to do so. The biggest issue is that my solvers finds literally everything (even multiloop broken wings, I have discovered (grouped broken wings??)). However, the solver is not aware of the way we define patterns and chains so it needs to be told, for which I have an after the fact recognizer. The recognizer is rule based so rules can be added any time.
What would be interesting is, what portion of the logic used to solve a puzzle can be classified as nrctz chains, etc.
My solver is very interactive, it has a 3D editor where I can draw any kind of logic, which is analyized on the spot. In one mode, you can enter sets (these define a group of candidates) and the analyzer will produce the cover sets, eliminations, legal permutations etc. Its great for asking what if questions. I can also pull a piece of logic from a puzzle and work on that.
Not a lot. I was surprised I could "cut and paste" your first order logic into a second order form. This comment reflects the only small difference I could see. I'm beginning to think that first order and second order logic are less different that I had imagined.
[...] => 2 questions. 1) Once an elimination has been made, this changes the sets and linksets for further potential eliminations identified in the first step. Are such changes propagated in the justifications of the further eliminations?
Yes, they are, meaning I start from scratch for the next elimination.
In SudoRules, I avoid "ghosts". All eliminations that'd be justified by candidates already eliminated are discarded. I've proven that there is always a simpler rule that still applies to justify these eliminations. This is intimately related to the confluence property of my theories. I think you have the same with yours.
I have always assumed this to be the case, without proof, i.e., that an elimination can open new opportunities to eliminate other candidates that could not be cleared before, or in your words, open shorter paths. (I now see that these are almost your exact words below). Further, doesn't this imply that given a group of candidates that cause an elimination, if one or more of the candidates is removed then the remaining candidates (alone) will still cause the same elimination?
2) Once an elimination has been made, this produces new sets and linksets for additional potential eliminations not available in the first step (which may be simpler than those already available). Do you restart the first step after each elimination?
Yes.
If, instead of nrczt-chains, one considers the usual AICs with ALSs (which have roughly the same resolution power as nrczt), things are more complex from the beginning, because there are two parameters: length of the chains and maximum size of the ALSs. I'd like to make the same statistical computations as I've done for nrczt, but as ALSs are not implemented in SudoRules, I can't. It seems no existing solver can do such computations.
This case seems closer to yours. But you have one more parameter: rank. Could your solver analyse large collections of puzzles and compute the mean number of patterns necessary to find a solution, for each choice of the parameters {rank, max size of the sets, nb of candidates,...}?
Yes, in principle solver 1 can do that kind of stastical work, but I have not configured it to do so. The biggest issue is that my solvers finds literally everything (even multiloop broken wings, I have discovered (grouped broken wings??)). However, the solver is not aware of the way we define patterns and chains so it needs to be told, for which I have an after the fact recognizer. The recognizer is rule based so rules can be added any time.
What would be interesting is, what portion of the logic used to solve a puzzle can be classified as nrctz chains, etc.
Allan Barker wrote:
I took your elimination above and entered it into my solver by placing a set for each of your nine {....} terms and the solver completed the logic producing the elimination shown below.
The linkset are added automatically?
My solver is very interactive, it has a 3D editor where I can draw any kind of logic, which is analyized on the spot. In one mode, you can enter sets (these define a group of candidates) and the analyzer will produce the cover sets, eliminations, legal permutations etc. Its great for asking what if questions. I can also pull a piece of logic from a puzzle and work on that.
Allan Barker wrote:
It also decided it did not need a set for n6{r3c5 r4c5}, only the nodes.
Does this mean anything special??
Not a lot. I was surprised I could "cut and paste" your first order logic into a second order form. This comment reflects the only small difference I could see. I'm beginning to think that first order and second order logic are less different that I had imagined.
- Allan Barker
- Posts: 266
- Joined: 20 February 2008
49 posts
• Page 1 of 4 • 1, 2, 3, 4

