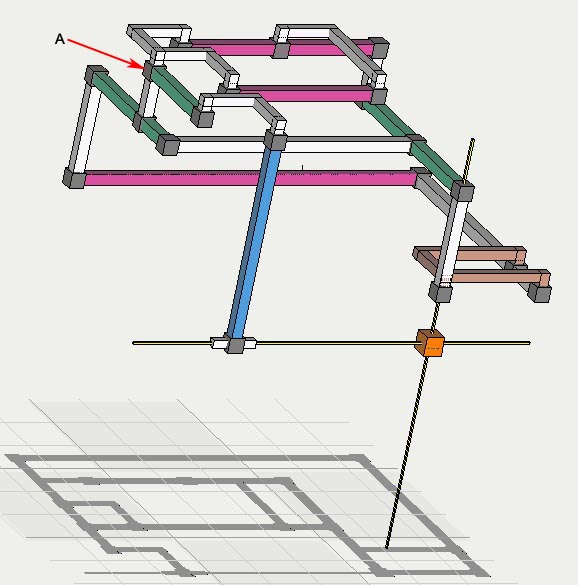
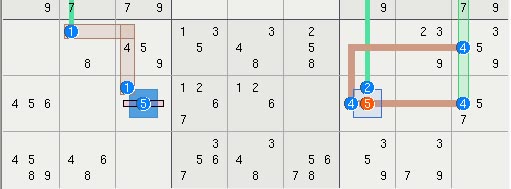
The Idea of Uniform Rank[Edit: replace previous argument on uniform rank with revised version. 3-6-08]
A key question about Sudoku set logic principles is, why would logic work in a way that guarantees a uniform rank over some region? In some ways, this seems counterintuitive, especially thinking about first order logic.
There is in fact a rational for such an effect, which is based on the logical permutations of candidates.
Given a rank 1 structure with 10 sets 11 linksets, the covering set principle says any two linksets must have at least one candidate, which is logically correct. But what makes sure there is always an arrangement of candidates that fulfills this requirement? Candidates are possibilities. Without constraints, all permutations or arrangements of candidates are possible, about one billion for this size problem. The number is much smaller because constraints remove most of them but without a constraint, or reason not to be there, all permutations are possible, and will be there. In this sense, the mathematics of combinorics fills every possible configuration that is not invalid, everywhere in the structure.
This turns the argument upside down, rather than why would a particular candidate or configuration be there, the correct question is why would it not be there? In the current example, if any two sets did not contain a candidate, that configuration must be invalid because it would force two candidates into one of the other sets.
In all cases, the areas presumed to have uniform rank are ones that also have uniform constraints. The rank rules require that each candidate is contained in only one set in each group, every candidate is in both groups, and no sets in the same group can overlap. When all permutations of an area with uniform constraints is considered, it probably should have uniform rank.
Although this does not prove anything, all things considered uniform rank seems reasonable.
[8-6-08]
Uploaded major revision of
SudokuOne Web Site. Main differences are:
. Much shorter, the entire set theory derivation and explanation is now on one page.
. A new section with many simple examples of set theory principles.
. Full attention to previously sketchy areas, i.e., triplets, rank zones, summing of rank effects.
As usual, all feedback is welcome. rab.