The New Sudoku Players' Forum

[HATMAN]

Semi-Symmetric Killer 1

Has anything been done on semi-symmetry? Where numbers are in pairs (with an odd one in r5c5) and if a cell contains a number the opposite cell must contain that number or its partner?

I've just put up a killer on this basis on the assassin site, here it is below.

This is a simple killer however the solution is semi-symmetrical. There are four unknown number pairs and an odd number (which of course goes in r5c5).
Each number pair is semi-symmetrical, consider for example that the number pair is 4,7, so if r3c1 contains a 7 then r7c9 must contain a 4 or a 7.

So deduce the number pairs and in parallel solve the sudoku.

Both solvers actually solve this directly SS gives it 3.35 and JS uses 41 fishes.

Using the semi-symmetry I would guess it is at or below difficulty 1.0.

[HATMAN]

Semi-symmetric Vanilla 2 and 2H

This is a plain vanilla Sudoku however the solution is semi-symmetrical. There are four unknown number pairs and an odd number (which of course goes in r5c5).
Each number pair is semi-symmetrical, consider for example that the number pair is 4,7, so if r3c1 contains a 7 then r7c9 must contain a 4 or a 7.

Semi-symmetric Vanilla 2

No fishes are needed.



Semi-symmetric Vanilla 2H

Some fishes are required.



Code:
8.......2.4...617..........4...27.9......4..7.8.....1....3....1..1..83.5......7..

[Wecoc]

Has anything been done on semi-symmetry?

I've been playing around a bit with Symmetry and Semi-symmetry (mainly for aesthetic purposes, not as a restriction) on some of my puzzles.
My solver has a method that tests the symmetry:

Hidden Text: Show

Code: Select all

class Sudoku
  #-----------------------------------------------------------------
  # * Find Symmetry Counterparts
  #-----------------------------------------------------------------
  def find_symmetry_cp(sym)
    result = {}
    # For digits 1 to 9
    for i in 1..9
      ary = []
      # For every box
      for box in 0...9
        # Search the value in every cell of the box
        for dy in 0...3
          for dx in 0...3
            x = dx + (box % 3 * 3)
            y = dy + ((box.to_f / 3).floor * 3)
            cell = get(x, y)
            if cell.solved && cell.values[0] == i
              # Get the counterpart and store it
              # Type of symmetry
              case sym
              when :rot # Rotational
                cp_x = 9 - x - 1
                cp_y = 9 - y - 1
              when :diag1 # Diagonal (\)
                cp_x = y
                cp_y = x
              when :diag2 # Diagonal (/)
                cp_x = 9 - y - 1
                cp_y = 9 - x - 1
              end
              ary.push(get(cp_x, cp_y).values[0])
            end
          end
        end
      end
      result[i] = ary
    end
    return result
  end
end

I checked some puzzles with that.

Example 1 - Rotational Symmetry (Non-consecutive Anti-Knight by Rishi Puri)

Code: Select all

973518264425963718861427953316842597758396142294751386649275831182639475537184629

Rotational:
1 => 8,8,8,8,8,8,8,8,8
2 => 7,7,7,7,7,7,7,7,7
3 => 6,6,6,6,6,6,6,6,6
4 => 5,5,5,5,5,5,5,5,5
5 => 4,4,4,4,4,4,4,4,4
6 => 3,3,3,3,3,3,3,3,3
7 => 2,2,2,2,2,2,2,2,2
8 => 1,1,1,1,1,1,1,1,1
9 => 9,9,9,9,9,9,9,9,9

Diagonal 1:
1 => 1,7,8,9,1,7,6,7,6
2 => 2,8,6,8,7,8,5,5,5
3 => 8,9,7,5,4,5,8,4,4
4 => 7,6,5,7,3,3,7,6,3
5 => 6,3,2,6,6,2,4,3,2
6 => 5,5,1,4,5,4,2,9,1
7 => 4,4,4,1,2,1,3,1,7
8 => 3,2,3,2,8,9,1,2,8
9 => 9,1,9,3,9,6,9,8,9

Diagonal 2:
1 => 8,2,1,9,8,2,3,2,3
2 => 7,1,3,1,2,1,4,4,4
3 => 1,9,2,4,5,4,1,5,5
4 => 2,3,4,2,6,6,2,3,6
5 => 3,6,7,3,3,7,5,6,7
6 => 4,4,8,5,4,5,7,9,8
7 => 5,5,5,8,7,8,6,8,2
8 => 6,7,6,7,1,9,8,7,1
9 => 9,8,9,6,9,3,9,1,9

Example 2 - Symmetry on Both Diagonals (Wecoc's puzzle August 10, 2019 by Wecoc)

Code: Select all

176932584928145367453876219715384692369527841284691735832459176541763928697218453

Rotational:
1 => 3,3,3,3,3,3,3,3,3
2 => 2,2,2,2,2,2,2,2,2
3 => 1,1,1,1,1,1,1,1,1
4 => 6,6,6,6,6,6,6,6,6
5 => 7,7,7,7,7,7,7,7,7
6 => 4,4,4,4,4,4,4,4,4
7 => 5,5,5,5,5,5,5,5,5
8 => 9,9,9,9,9,9,9,9,9
9 => 8,8,8,8,8,8,8,8,8

Diagonal 1:
1 => 1,1,1,1,1,1,1,1,1
2 => 2,2,2,2,2,2,2,2,2
3 => 3,3,3,3,3,3,3,3,3
4 => 6,6,6,6,6,6,6,6,6
5 => 8,8,8,8,8,8,8,8,8
6 => 4,4,4,4,4,4,4,4,4
7 => 9,9,9,9,9,9,9,9,9
8 => 5,5,5,5,5,5,5,5,5
9 => 7,7,7,7,7,7,7,7,7

Diagonal 2:
1 => 3,3,3,3,3,3,3,3,3
2 => 2,2,2,2,2,2,2,2,2
3 => 1,1,1,1,1,1,1,1,1
4 => 4,4,4,4,4,4,4,4,4
5 => 9,9,9,9,9,9,9,9,9
6 => 6,6,6,6,6,6,6,6,6
7 => 8,8,8,8,8,8,8,8,8
8 => 7,7,7,7,7,7,7,7,7
9 => 5,5,5,5,5,5,5,5,5

Example 3 - Semi Rotational Symmetry (Semi-Symmetric Killer 1, in this topic)

Code: Select all

163789452542163789789452163475218396396574218218396574821645937937821645654937821

Rotational:
1 => 1,1,1,9,9,9,1,1,1
2 => 6,6,6,6,6,6,6,6,6
3 => 8,8,8,8,8,8,8,8,8
4 => 4,5,5,4,5,4,5,5,4
5 => 5,4,4,5,4,5,4,4,5
6 => 2,2,2,2,2,2,2,2,2
7 => 7,7,7,7,7,7,7,7,7
8 => 3,3,3,3,3,3,3,3,3
9 => 9,9,9,1,1,1,9,9,9

Diagonal 1:
1 => 1,7,1,3,5,2,1,7,1
2 => 8,8,6,9,2,4,7,1,5
3 => 7,1,5,8,8,6,8,8,6
4 => 4,5,8,7,9,7,9,2,4
5 => 6,6,9,4,1,5,3,5,2
6 => 5,9,7,5,6,9,2,3,3
7 => 3,4,2,1,7,1,6,4,8
8 => 2,3,3,2,3,3,4,9,7
9 => 9,2,4,6,4,8,5,6,9

Diagonal 2:
1 => 1,7,1,8,4,6,1,7,1
2 => 3,3,2,9,6,5,7,9,5
3 => 7,9,4,3,3,2,3,3,2
4 => 4,5,3,7,1,7,9,6,4
5 => 2,2,9,5,9,4,8,5,6
6 => 5,1,7,4,2,9,6,8,8
7 => 8,4,6,1,7,1,2,4,3
8 => 6,8,8,6,8,8,5,1,7
9 => 9,6,5,2,5,3,4,2,9

Other examples:
- Rotational Symmetry {fixed to also have similar 'means' on 90º} (Meandoku by Wecoc)

Code: Select all

853164297647932815192875364315649782728351649469728531281596473536417928974283156

If a "Semi-symmetric" Sudoku is one that has either its partner or itself in the opposite side, the definition could be extended for those where 2 partners and itself are possible for each digit, etc.

These ones have quite a symmetrical grid but would fall into this category:
- 'A bit symmetrical' Rotational Symmetry (Partial Killer by Wecoc)

Code: Select all

126479853439865712785132469642783195893516247571294386964321578217658934358947621

- 'A bit symmetrical' Rotational Symmetry (First Hidden Skyscraper Sudoku by Laura Soler)

Code: Select all

482537196963241857175986432347862915618495723529713648234679581856124379791358264

[EDIT] I'll add some more examples.

- 90º Rotational Symmetry (Assassin 123 "Roulette" by Udosuk)

Code: Select all

654132978912687435387945162495216783168753249723498516849561327576324891231879654

- 90º Rotational Symmetry (Example solution by Wecoc, based on a Shuriken (???) puzzle by Red Ed)

Code: Select all

587134296946728315123956478375461982218597634469382751652879143731645829894213567
685429713217563489439871265862314957974258631351697842548932176126745398793186524

- Rotational Symmetry with equal boxes (Riddle of Sho)

Code: Select all

123978645456312897789564231645123978897456312231789564978645123312897456564231789

- Diagonal Symmetry (Shining Mirror by Mauricio)

Code: Select all

879431652623597148154268793432816579517943826968752431796384215341625987285179364

Also, using the number of unique digits in each case you could define a Symmetrical "index" for each type

[m_b_metcalf]

Has anything been done on semi-symmetry? Where numbers are in pairs (with an odd one in r5c5) and if a cell contains a number the opposite cell must contain that number or its partner?

This topic has occasionally surfaced in the Patterns Game, where generationg symmetric puzzles is often a good path to a decent seed. However, knowing that the solution grid is symmetric is not necessarily helpful in manually solving when the dispostion of the clues is too: you have no pair clue to work on. Here's an example from the current Game:

Code: Select all

 . . . . . 1 . . .
 . . 2 . 3 4 . . 5
 . 6 . 7 5 . 4 . .
 8 . . . . . . 1 3
 . . 6 . . . 9 . .
 2 5 . . . . . . 7
 . . 4 . 1 8 . 9 .
 1 . . 4 2 . 3 . .
 . . . 5 . . . . . 

Where do you start?

Regards,

Mike

P.S. Having just written that it's obvious where you start, but I'll leave the question there. But here's a better example:

Code: Select all

 . . . . . 3 . . .
 . . 4 . 1 9 . . 8
 . 1 . 5 . . 2 . .
 9 . . . . . . 3 5
 . . 3 . 6 . 7 . .
 4 7 . . . . . . 1
 . . 8 . . 4 . 9 .
 2 . . 1 9 . 5 . .
 . . . 7 . . . . .

[Wecoc]

I've updated my last post with other examples I know. Some might be interesting, particularly the non-classic sudoku examples that use this type of symmetry.
Best topic I could find about this is that oldie: About Red Ed's Sudoku symmetry group, especially the table in the very start, extended here.

But all that focuses on full symmetry, and as counterwise as it may seem, I believe semi-symmetry is more limited.
Can a puzzle have 90º rotational semi-symmetry? Or diagonal semi-symmetry? And better not talk about hybrids like rotational symmetry + diagonal semi-symmetry or something like that...
Based on a few tests I made in JSudoku, I don't think any of that is possible

-----

My solver now includes the semi-symmetry constrain.

Code: Show

Code: Select all

class Sudoku_SemiSymmetry < Sudoku
  def initialize(*args)
    super(*args)
    @pairings = {}
    @pairings.default = 0
    @symmetry_type = :rot
  end
 
  def iterate
    super
    # If there are no changes after default techniques,
    # apply semi symmetry constrain
    if self == @current
      iterate_semi_symmetry
      #return if self != @current
    end
  end
 
  def get_counter_coords(x, y)
    case @symmetry_type
    when :rot # Rotational
      cp_x = 9 - x - 1
      cp_y = 9 - y - 1
    when :diag1 # Diagonal (\)
      cp_x = y
      cp_y = x
    when :diag2 # Diagonal (/)
      cp_x = 9 - y - 1
      cp_y = 9 - x - 1
    when :rot90 # Rotational 90º
      cp_x = y
      cp_y = 9 - x - 1
    end
    return [cp_x, cp_y]
  end
 
  def iterate_semi_symmetry
    for iy in 0...9
      for ix in 0...9
        cell = get(ix, iy)
        next if !cell.solved
        cp_x, cp_y = *get_counter_coords(ix, iy)
        check = get(cp_x, cp_y)
        if check.solved
          if check.values[0] != cell.values[0]
            # Define pairing for each value
            if @pairings[cell.values[0]] == 0
              @pairings[cell.values[0]] = check.values[0]
            end
          end
        else
          if @pairings[cell.values[0]] != 0
            # Reduce its candidates to [self, pairing]
            check.values &= [cell.values[0], @pairings[cell.values[0]]]
          end
        end
      end
    end
    if self != @current
      @current = self.clone
      check_solved
    end
  end
end

Solution of Semi-symmetric Vanilla 2 & 2H

Solution: Show

Code: Select all

896|173|452
542|986|173
137|452|968
---+---+---
413|827|596
629|514|837
785|639|214
---+---+---
978|345|621
261|798|345
354|261|789

[HATMAN]

Wecoc

Semi-symmetry is definitely more limited. With an NC puzzle there are plenty of purely asymmetric solutions but I have not been able to find any fully semi-symmetric ones (i.e. at least one number is paired with itself). This analysis has been semi-manual so no guarantees.

I'll think about the other symmetries you suggest. Some of the symmetries will of course only allow asymmetry.

I had thought of larger groupings, but my feeling is that the puzzle would get too confused.

Maurice

[Wecoc]

With an NC puzzle there are plenty of purely asymmetric solutions but I have not been able to find any fully semi-symmetric ones (i.e. at least one number is paired with itself). This analysis has been semi-manual so no guarantees.

I found one of those

Code: Select all

..............1...1.....9.....2...9...4...3...7...5.....9.....1...1..............
725849163948361725163527948816273594594618372372495816639752481257184639481936257

Rotational:
1 => 1,1,1,1,1,1,1,1,1
2 => 5,5,5,5,5,5,5,5,5
3 => 4,4,4,4,4,4,4,4,4
4 => 3,3,3,3,3,3,3,3,3
5 => 2,2,2,2,2,2,2,2,2
6 => 8,8,8,8,8,8,8,8,8
7 => 7,7,7,9,9,9,7,7,7
8 => 6,6,6,6,6,6,6,6,6
9 => 9,9,9,7,7,7,9,9,9

[EDIT] Variants of the same solution that are still valid NC (Non-Consecutive Adjacent Cells) obtained swapping the digits.
The number of valid NC solutions (variants) for this grid would be twice as many because you can also get the inverse of each one (1<>9, 2<>8, 3<>7, 4<>6, 5<>5) and it will still be valid.

Code: Select all

725849163948361725163527948816273594594618372372495816639752481257184639481936257 Wecoc NC #1
925847163748361925163529748816293574574618392392475816637952481259184637481736259 (7<>9)
715849263948362715263517948826173594594628371371495826639751482157284639482936157 (2<>1)
725849361948163725361527948836271594594638172172495836619752483257384619483916257 (1<>3)
915847263748362915263519748826193574574628391391475826637951482159284637482736159 (7<>9, 2<>1)
925847361748163925361529748836291574574638192192475836617952483259384617483716259 (7<>9, 1<>3)
735819462918264735462537918846372591591648273273195846629753184357481629184926357 (2<>3, 4<>1)
935817462718264935462539718846392571571648293293175846627953184359481627184726359 (7<>9, 2<>3, 4<>1)
715849362948263715362517948836172594594638271271495836629751483157384629483926157 (2<>1, 1<>3, 3<>2)
752639184936481752184257936618574293293816475475392618849725361527163849361948527 (2<>5, 8<>6, 4<>3)
952637184736481952184259736618594273273816495495372618847925361529163847361748529 (7<>9, 2<>5, 8<>6, 4<>3)
915847362748263915362519748836192574574638291291475836627951483159384627483726159 (7<>9, 2<>1, 1<>3, 3<>2)
715839462938264715462517938846172593593648271271395846629751384157483629384926157 (2<>1, 4<>3, 1<>4, 3<>2)
751639284936482751284157936628574193193826475475391628849715362517263849362948517 (2<>5, 5<>1, 8<>6, 4<>3, 1<>2)
751629483926384751483157926648573192192846375375291648839715264517462839264938517 (2<>5, 5<>1, 8<>6, 4<>2, 1<>4)
752619384916483752384257916638574291291836475475192638849725163527361849163948527 (2<>5, 8<>6, 4<>1, 1<>3, 3<>4)
915837462738264915462519738846192573573648291291375846627951384159483627384726159 (7<>9, 2<>1, 4<>3, 1<>4, 3<>2)
951637284736482951284159736628594173173826495495371628847915362519263847362748519 (7<>9, 2<>5, 5<>1, 8<>6, 4<>3, 1<>2)
951627483726384951483159726648593172172846395395271648837915264519462837264738519 (7<>9, 2<>5, 5<>1, 8<>6, 4<>2, 1<>4)
753629481926184753481357926648571392392846175175293648819735264537462819264918537 (2<>5, 5<>3, 8<>6, 4<>2, 1<>4, 3<>1)
952617384716483952384259716638594271271836495495172638847925163529361847163748529 (7<>9, 2<>5, 8<>6, 4<>1, 1<>3, 3<>4)
751629384926483751384157926638574192192836475475291638849715263517362849263948517 (2<>5, 5<>1, 8<>6, 4<>2, 1<>3, 3<>4)
953627481726184953481359726648591372372846195195273648817935264539462817264718539 (7<>9, 2<>5, 5<>3, 8<>6, 4<>2, 1<>4, 3<>1)
173859426958624173426371958842716395395248617617593842269137584731485269584962731 (7<>1, 2<>7, 5<>3, 4<>5, 1<>4, 6<>2, 3<>6)
951627384726483951384159726638594172172836495495271638847915263519362847263748519 (7<>9, 2<>5, 5<>1, 8<>6, 4<>2, 1<>3, 3<>4)
137269485962584137485731962248315796796842513513697248859173624371426859624958371 (7<>1, 2<>3, 5<>7, 8<>2, 4<>6, 1<>4, 6<>8, 3<>5)
973851426158624973426379158842796315315248697697513842261937584739485261584162739 (7<>9, 2<>7, 5<>3, 4<>5, 9<>1, 1<>4, 6<>2, 3<>6)
137269584962485137584731962258314796796852413413697258849173625371526849625948371 (7<>1, 2<>3, 5<>7, 8<>2, 4<>6, 1<>5, 6<>8, 3<>4)
937261485162584937485739162248395716716842593593617248851973624379426851624158379 (7<>9, 2<>3, 5<>7, 8<>2, 4<>6, 9<>1, 1<>4, 6<>8, 3<>5)
937261584162485937584739162258394716716852493493617258841973625379526841625148379 (7<>9, 2<>3, 5<>7, 8<>2, 4<>6, 9<>1, 1<>5, 6<>8, 3<>4)

[HATMAN]

Semi-Symmetrical NC Killer 2

Thank you Wecoc, and it is also a nice puzzle. I tried leaving out givens but in the ones I checked it was either non-unique or only recursively solvable.
So do we have a term for a puzzle that is not numerically minimal but is minimal in terms of solvability?

With your table is that just the variants from your original solution or are you saying more?

Using your puzzle I made the following killer which is reasonably hard.

[Wecoc]

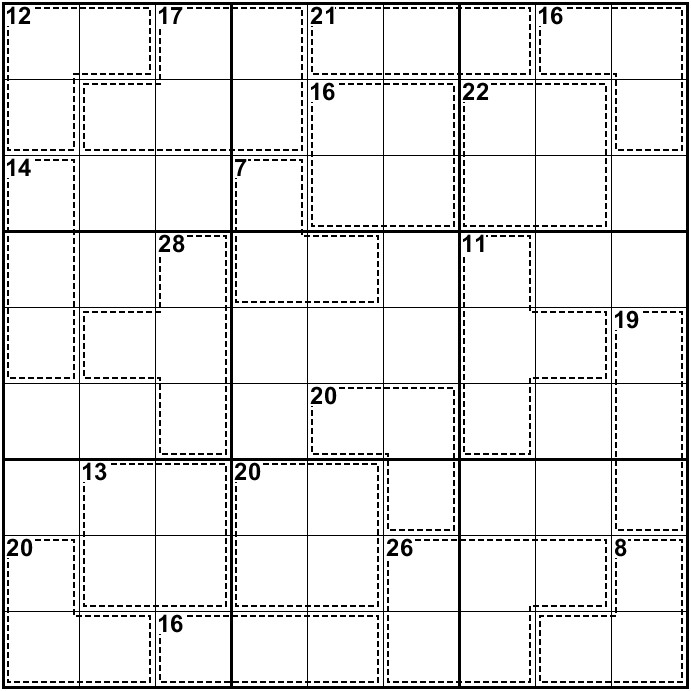
With your table is that just the variants from your original solution or are you saying more?

That table contains all the variants of my original solution that are still valid NC, indicating which digits I interchanged.
Those are only half of them, because if a grid (N) 1-2-3-4-5-6-7-8-9 is a valid NC, the grid (10-N) 9-8-7-6-5-4-3-2-1 still has that property, so I didn't include those.

----

We could understand a semi-symmetrical grid as a grid that has both symmetric pairs (including the digit paired with itself) and semi-symmetric pairs.
Based on that, I found there are 2 types of semi-symmetric pairs.

- Disconnected blocks from a symmetric pair (DSP)

The 79s in my last puzzle is an example of that.
If you try this puzzle you will notice it has 4 valid solutions, 2 of them are symmetrical, and the other 2 are semi-symmetrical.
.2584.163.48361.2516352..4881629357457461839239247581663..5248125.18463.481.3625.

- Connected blocks in a specific 'semi-symmetric' pair (CSSP)

In this case you can't get a symmetrical puzzle, the distribution is specifically semi-symmetrical.
The 45s in Semi-symmetric Vanilla 2 & 2H would be an example of that.
896173..2..2986173137452968.13827.9662951483778.63921.9783456212617983..3..261789

We can do the inverse step and get new valid semi-symmetrical solutions from both symmetrical and semi-symmetrical grids, if some of their pairs has disconnected blocks.
I just did that with some of the examples we've already seen to get some valid semi-symmetrical grids:

Code: Select all

654172938912683475783945162495216783168357249327498516849561327536724891271839654 123 Roulette        {37-DSP}
123978645654312897789564231465123978897456312231789564978645123312897456546231789 Riddle of Sho       {46-DSP}
183972645456318297729564831645183972297456318831729564978645123312897456564231789 Riddle of Sho       {28-DSP}
435981276712634895968752431849267513376145982251893647524318769197426358683579124 m_b_metcalf (First) {69-DSP}
725849163948361725163527948816293574574618392392475816639752481257184639481936257 Wecoc NC #1(')      {79-DSP}

And yes, in this case Wecoc NC #1(') is still a valid NC grid.

Some other examples of semi-symmetrical grids I found while trying this in JSudoku:

Code: Select all

265748931347291685981536274756324819423819756819657423632475198594182367178963542 Wecoc Vanilla #1 {25-DSP}
483172956729658314561943872378426591295317648146589237832794165917865423654231789 Wecoc Vanilla #2 {28-DSP}
487635129125489637639127485251368974974251368368974251593712846746893512812546793 Wecoc Vanilla #3 {67-CSSP}