The New Sudoku Players' Forum

[StrmCkr]

time for some group attack
to bring down the:

Savage attaking Monster
{ a hand build puzzle by strmckr} ER: 8.4

Code: Select all

 *-----------*
 |5..|...|..9|
 |.2.|...|.1.|
 |..8|.4.|3..|
 |---+---+---|
 |6..|..2|...|
 |...|.5.|1..|
 |..4|7.3|...|
 |---+---+---|
 |..3|1..|8..|
 |.6.|...|.2.|
 |9..|..6|..5|
 *-----------*

Code: Select all

*-----------------------------------------------------------------------------*
 | 5       34      167     | 238     23678   178     | 2467    478     9       |
 | 34      2       679     | 3589    36789   5789    | 4567    1       478     |
 | 17      179     8       | 2569    4       1579    | 3       567     267     |
 |-------------------------+-------------------------+-------------------------|
 | 6       135789  1579    | 489     189     2       | 4579    45789   3478    |
 | 2378    3789    279     | 4689    5       489     | 1       46789   234678  |
 | 128     1589    4       | 7       1689    3       | 2569    589     28      |
 |-------------------------+-------------------------+-------------------------|
 | 247     457     3       | 1       279     4579    | 8       4679    467     |
 | 478     6       57      | 34589   3789    45789   | 479     2       1       |
 | 9       1478    127     | 248     278     6       | 47      3       5       |
 *-----------------------------------------------------------------------------*

[Allan Barker]

Strmckr, Nice puzzle. It has more "pretty" logic than most computer generated puzzles.

Something that looks almost like a 4-String Kite, first I have ever seen.

(2)r6c7=(2)r1c7-(2)r3c9=(2-6)r3c4=(6)r5c4-(6)r6c5=(6-2)r6c7.
or
(6)r6c7=(6)r21c7-(6)r3c98=(6-2)r3c4=(2)r3c9-(2)r1c7=(2-6)r6c7.

.
.

.

[ronk]

This is a 4-String Kite, first I have ever seen.

(6)r6c7=(6)r21c7-(6)r3c98=(6-2)r3c4=(2)r3c9-(2)r1c7=(2-6)r6c7.

I found the above as well ... and think it should be called a hidden w-ring. I illustrated w-wing variants here and later added an (unhidden) w-ring example.

[Allan Barker]

I found the above as well ... and think it should be called a hidden w-ring. I illustrated w-wing variants here and later added an (unhidden) w-ring example.

I was thinking more that it looked like a 4-String Kite, admittedly its not logically the same as a 2-string kite, so I changed my wording a bit.

Of course, it just might be a doubly-lin...... nah

[aran]

Code: Select all

*-----------------------------------------------------------------------------*
 | 5       34      167     | 238     23678   178     | 2467    478     9       |
 | 34      2       679     | 3589    36789   5789    | 4567    1       478     |
 | 17      179     8       | 2569    4       1579    | 3       567     267     |
 |-------------------------+-------------------------+-------------------------|
 | 6       135789  1579    | 489     189     2       | 4579    45789   3478    |
 | 2378    3789    279     | 4689    5       489     | 1       46789   234678  |
 | 128     1589    4       | 7       1689    3       | 2569    589     28      |
 |-------------------------+-------------------------+-------------------------|
 | 247     457     3       | 1       279     4579    | 8       4679    467     |
 | 478     6       57      | 34589   3789    45789   | 479     2       1       |
 | 9       1478    127     | 248     278     6       | 47      3       5       |
 *-----------------------------------------------------------------------------*

1. (another way of seeing that opening move of Allan/Ronk) : hidden triple : 489b5=6r5c4-6r6c5=(6-2)r6c7=2r1c7-2r3c9=(2-6)r3c4=6r5c4-489b5 : loop =><59>r6c7, r3c4
2. 5r3c8=267r3c489-7r3c12=67r12c3-(67=5)r8c3-5r8c46=5r7c6-5r3c6=5r3c8 :=> r3c8=5

[Steve K]

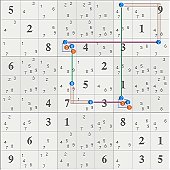
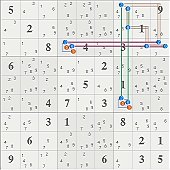
Thank-you StrmCkr for a very interesting puzzle. After the excellent move above, I found another rather interesting move.
SAM
1) ssts
2) (2)r6c7=-r1c7-r3c9=(2-6)r3c4=r3c89-r12c7=(6)r6c7 loop =>r6c7,r3c4<>59
3) (5sf)r3c68,r6c82,r7c26 => r28c6,r4c28<>5
as noted above gets us to this point

Code: Select all

 
 *-----------------------------------------------------------------------------*
 | 5       34      167     | 238     23678   178     | 2467    478     9       |
 | 34      2       679     | 3589    36789   789     | 4567    1       478     |
 | 17      179     8       | 26      4       1579    | 3       567     267     |
 |-------------------------+-------------------------+-------------------------|
 | 6       13789   1579    | 489     189     2       | 4579    4789    3478    |
 | 2378    3789    279     | 4689    5       489     | 1       46789   234678  |
 | 128     1589    4       | 7       1689    3       | 26      589     28      |
 |-------------------------+-------------------------+-------------------------|
 | 247     457     3       | 1       279     4579    | 8       4679    467     |
 | 478     6       57      | 34589   3789    4789    | 479     2       1       |
 | 9       1478    127     | 248     278     6       | 47      3       5       |
 *-----------------------------------------------------------------------------*


4) [[(9):r3c6=r3c2-r2c3=r4c3]=(9-2)r5c3=(2-1)r9c3=[(1):r4c3=r1c3-r3c12=r3c6]]=> (19)r3c6=(19)r4c3 => (19)r3c6=(19-5)r4c3=(5)r8c3-r7c2=(5)r7c6 => r3c6<>5 (of course, one could just as easily eliminate (5)r4c3) => some singles.

step as a pigeonhole matrix (each column except first is a wis, each row a sis, nxn matrix =>conclusion is first column is a sis) (also, sis are labelled to the far left of matrix for clarity) => r3c6<>5

Code: Select all

 
5r7  c6  c2                     
5c3      r8  r4                 
1c3          r4  r9  r1           
1r3  c6             c12           
2c3              r9      r5         
9c3          r4          r5  r2     
9r3  c6                      c2   


In any event, whatever we will call the first step involving the loop in candidates 26, this step contains an almost almost loop of the same variety involving candidates 19. Call it 2 degrees of freedom. The 2s is column 3 subtract one degree of freedom. This leaves the 5's with too little freedom to exist at both of the two loop endpoints, r3c6 and r4c3.

A shorter view of the same elimination: (uses one less sis)
(5)r7c6=(5)r7c2-(5=7)r8c3-(7)r12c3=[(1)r3c6=(1)r3c12-(1=6)r1c3-(6=9)r2c3-(9)r3c2=(9)r3c6 loop] =>r3c6<>5
With this view, the Almost Hub rim 2 spokes has one degree of freedom in the rim, AALS 1679 r12c3. The beginning of the chain above shows where that one degree of freedom might lead.
Below, find a pigeonhole matrix that describes the shorter view:

Code: Select all

5r7 c6  c2
r8c3     5   7
r2c3         7   6   9
r1c3         7   6       1
1r3 c6                 c12
9r3 c6              c2

[storm_norm]

AHH! I wish I would have posted before Steve K because this thread looks so much more enticing when Steve K is shown as the last poster, no?
at any rate.
this is my stream-of-thought path through the maze.
1...swordfish 6, r6c89, r4c89, r2c9, r2c8, r12c4 all not 6
2...loop: (2)r3c9 = (2-6)r3c4 = (6)r5c4 - (6)r6c5 = (6-2)r6c7 = (2)r1c7; r3c4|r6c7 <> 59
3...swordfish 5, r2c6, r4c2, r4c8, r8c6 all not 5
4...(2)r5c9 = (2-6)r6c7 = (6)r6c5 - (6)r5c4 = (6-2)r3c4 = (2)r3c9; r5c9 <> 2
5...(7=5)r8c3 - (5)r3c3 = (5-9)r4c7 = (9)r8c7; r8c7 <> 7
6...(7=1)r3c1 - (1=8)r6c1 - (8)r8c2 = (8-1)r9c2 = (1-2)r9c3 = (2)r7c1; r7c1 <> 7
7...(26)r3c49 = (7)r3c9 - (7)r3c12 = (7)r12c3 - (7=5)r8c3 - (5)r8c4 = (5)r2c4 - (5)r2c7 = (5)r3c8; r3c8 <> 6
8...(7)r12c3 = (7)r3c12 - (7=5)r3c8 - (5)r3c6 = (5)r7c6 - (5)r7c2 = (5)r8c3; r8c3 <> 7
9...(1=8)r6c1 - (8)r8c1 = (8-1)r9c2 = (1)r9c3; r4c3 <> 1
10...(7=9)r4c3 - (9)r4c4 = (4-6)r5c4 = (6-1)r6c5 = (1)r6c1 - (1=7)r3c1; r5c1 <> 7
11...(7=1)r3c1 - (1)r6c1 = (1-6)r6c5 = (6-9)r5c4 = (9)r5c2 - (9)r3c2 = (9)r3c6; r3c6 <> 7
12...(6)r1c3 = (6-9)r2c3 = (9)r4c3 - (9)r4c4 = (9-6)r5c4 = (6)r3c4; r1c5 <> 6
13...(8=3)r5c1 - (3)r2c1 = (3)r1c2 - (3)r1c45 = (3-6)r2c5 = (6-1)r6c5 = (1)r6c1; r6c1 <> 8
14...kite 8 removes 8 from r1c5
15...(8=3)r5c1 - (3)r2c1 = (3-6)r2c5 = (6)r3c4 - (6=2)r3c9 - (2=8)r6c9; r5c89 <> 8
16...(4=8)r8c1 - (8=3)r5c1 - (3)r2c1 = (3)r1c2 - (3)r1c4 = (3)r8c4; r8c4 <> 4
17...(8=4)r5c6 - (4)r8c6 = (4)r9c4 - (4=7)r9c7 - (7=1)r9c3 - (1)r1c3 = (1)r1c6; r1c6 <> 8
18...loop: (8=4)r5c6 - (4)r8c6 = (4-8)r8c1 - (8)r5c1; r5c2|r5c4 <> 8
19...(4)r1c2 = (4)r2c1 - (4)r8c1 = (4)r8c6 - (4=8)r5c6 - (8)r6c5 = (8)r6c9 - (8)r2c9 = (8)r1c8; r1c8 <> 4
20...(ht347)r157c2 = (9)r5c2 - (9=7)r4c3; r4c2 <> 7
21...(7=4)r9c7 - (4)r9c4 = (4)r8c6 - (4=8)r8c1 - (8=3)r5c1 - (3=4)r2c1 - (4)1c2 = (4)r1c7; r1c7 <> 7
22...w-wing {4,7} removes 7 from r9c23
23...skyscraper 8 removes 8 from r5c6

[ronk]

Code: Select all

 
 *--------------------------------------------------------------------*
 | 5      34     167    | 238    23678  178    | 2467   478    9      |
 | 34     2      679    | 3589   36789  789    | 4567   1      478    |
 | 17     179    8      | 26     4      1579   | 3      567    267    |
 |----------------------+----------------------+----------------------|
 | 6      13789  1579   | 489    189    2      | 4579   4789   3478   |
 | 2378   3789   279    | 4689   5      489    | 1      46789  234678 |
 | 128    1589   4      | 7      1689   3      | 26     589    28     |
 |----------------------+----------------------+----------------------|
 | 247    457    3      | 1      279    4579   | 8      4679   467    |
 | 478    6      57     | 34589  3789   4789   | 479    2      1      |
 | 9      1478   127    | 248    278    6      | 47     3      5      |
 *--------------------------------------------------------------------*



4) [[(9):r3c6=r3c2-r2c3=r4c3]=(9-2)r5c3=(2-1)r9c3=[(1):r4c3=r1c3-r3c12=r3c6]]=> (19)r3c6=(19)r4c3 => (19)r3c6=(19-5)r4c3=(5)r8c3-r7c2=(5)r7c6 => r3c6<>5

I've found this format to be much easier to understand.

Code: Select all

At least one of any three candidates of an AALS must be true.

(15679)aals:r128c3
 ||
(9)r2c3 - (9)r3c2 = (9)r3c6
 ||
(1)r1c3 - (1)r3c12 = (1)r3c6
 ||
(5)r8c3 - (5)r7c2 = (5)r7c6 ==> r3c6<>5

[Luke]

Code: Select all

 
 *--------------------------------------------------------------------*
 | 5      34     167    | 238    23678  178    | 2467   478    9      |
 | 34     2      679    | 3589   36789  789    | 4567   1      478    |
 | 17     179    8      | 26     4      1579   | 3      567    267    |
 |----------------------+----------------------+----------------------|
 | 6      13789  1579   | 489    189    2      | 4579   4789   3478   |
 | 2378   3789   279    | 4689   5      489    | 1      46789  234678 |
 | 128    1589   4      | 7      1689   3      | 26     589    28     |
 |----------------------+----------------------+----------------------|
 | 247    457    3      | 1      279    4579   | 8      4679   467    |
 | 478    6      57     | 34589  3789   4789   | 479    2      1      |
 | 9      1478   127    | 248    278    6      | 47     3      5      |
 *--------------------------------------------------------------------*

I've found this format to be much easier to understand.

Code: Select all

At least one of any three candidates of an AALS must be true.

(15679)aals:r128c3
 ||
(9)r2c3 - (9)r3c2 = (9)r3c6
 ||
(1)r1c3 - (1)r3c12 = (1)r3c6
 ||
(5)r8c3 - (5)r7c2 = (5)r7c6 ==> r3c6<>5

You know Ron, your persistence is paying off…..for me at least. I compared this to another recent example, and between the two of them, the lights came on. (Here comes the part where I think out loud….)

You have constructed three small chains starting with members of the AALS, which is just a N+2 set. If all three endpoints can either see or pinch off an extra member candidate then there’s an elimination. Simpler in theory in practice, as you noted: “Now if I could just find one of these things on my own. ” (Here comes the part where I start guessing…)

It seems obvious then that at least one of any two candidates of an ALS must also be true. Then one would only have to find two little chains, much easier . Is this also done?

If one extends a net off an AALS, is that what is known as Kraken, or Kraken AALS? Or is just AALS good enough? (It was good enuf for you, which is good enuf for me…) What do you call two chains off of an ALS (if that’s a thing y’all do?) If the answer involves some controversy, forget I asked .

[aran]

Code: Select all

 
 *-----------------------------------------------------------------------------*
 | 5       34      167     | 238     23678   178     | 2467    478     9       |
 | 34      2       679     | 3589    36789   789     | 4567    1       478     |
 | 17      179     8       | 26      4       1579    | 3       567     267     |
 |-------------------------+-------------------------+-------------------------|
 | 6       13789   1579    | 489     189     2       | 4579    4789    3478    |
 | 2378    3789    279     | 4689    5       489     | 1       46789   234678  |
 | 128     1589    4       | 7       1689    3       | 26      589     28      |
 |-------------------------+-------------------------+-------------------------|
 | 247     457     3       | 1       279     4579    | 8       4679    467     |
 | 478     6       57      | 34589   3789    4789    | 479     2       1       |
 | 9       1478    127     | 248     278     6       | 47      3       5       |
 *-----------------------------------------------------------------------------*


step as a pigeonhole matrix (each column except first is a wis, each row a sis, nxn matrix =>conclusion is first column is a sis) (also, sis are labelled to the far left of matrix for clarity) => r3c6<>5

Code: Select all

 
5r7  c6  c2                     
5c3      r8  r4                 
1c3          r4  r9  r1           
1r3  c6             c12           
2c3              r9      r5         
9c3          r4          r5  r2     
9r3  c6                      c2   


Below, find a pigeonhole matrix that describes the shorter view:

Code: Select all

5r7 c6  c2
r8c3     5   7
r2c3         7   6   9
r1c3         7   6       1
1r3 c6                 c12
9r3 c6              c2

Indeed an interesting way of looking at it.
Those pigeon-hole matrices have their equivalent presentation in the world of base sets/cover sets eg
1st matrix
Cover for the base of 7 strong sets :
1b1, 9b1, 5b7, r3c6, r4c3, r5c3, r7c6, r9c3=8 strong sets.
=>rank 1 structure.
=>anything which removes 2 covers is false.
5r3c6 removes r3c6 and r7c6 : =><5>r3c6
2nd matrix
Cover for the base of 6 strong sets
1b1, 9b1, 5b7, 7c3, 6c3 (or 6b1), r3c6, r7c6=7 strong sets
=>rank 1 structure.
same conclusion as above.

[Allan Barker]

Those pigeon-hole matrices have their equivalent presentation in the world of base sets/cover sets eg ........

Here is an example base/cover set matrix for a slightly "less truthful" version of Steve's 6 truth elimination. The 5 truth solution uses box set 7B1 in place of an aals, but is otherwise about the same.. The xsudo output shows 5 strong and 6 weak sets (rank 1), thus the overlap of 3n6 and 5c6 eliminates 5r3c6. If the same logic was single digit, it might be called a Kraken fish.

Note, this kind of simple BC set matrix does not have a results column like the more powerful PM matrices but is often useful for drawing diagrams.

Code: Select all

     (3n6)  (3n2)  (3n1)  (5c6)  (5b7)  (7c3)

1R3: 1r3c6==1r3c2==1r3c1                      }
       |      |      |                        } AHS:(19)r3
9R3: 9r3c6==9r3c2    |                        }
       |      |      |                 7r2c3
7B1:   |    7r3c2==7r3c1===============7r1c3  }
       |                                 |    }
8N3:   |                        5r8c3==7r8c3  } Tenacular Kraken like extension
       |                          |           }
5R7:   |                 5r7c6==5r7c2         }
       |                   |
       |                   |
     5r3c6 ----------------+                  } 5<>r3c6 

Alas, Ronk's format is pretty easy to understand, this is my attempt to adapt the above to the same format where 7B1 works as an aahs.

Code: Select all

At least one of the three branches from 7B1 must be true

(7)b1           - same as an aahs
 ||
(7)r3c2 - (9)r3c2 = (9)r3c6
 ||
(7)r3c12- (1)r3c12 = (1)r3c6
 ||
(7)r12c3-(7=5)r8c3-(5)r7c2 = (5)r7c6 ==> r3c6<>5

[ronk]

If one extends a net off an AALS, is that what is known as Kraken, or Kraken AALS? Or is just AALS good enough?

I think an AALS is a Kraken ALS. An AAALS would be a Kraken ALS too. I much prefer AALS since 1) it's unambiguous, 2) it's shorter, and 3) searches on the Players' Forums using 'AALS' are more effective than searches using 'Kraken ALS'.

It seems obvious then that at least one of any two candidates of an ALS must also be true. Then one would only have to find two little chains, much easier . Is this also done?
...
What do you call two chains off of an ALS (if that’s a thing y’all do?)

Done all the time IMO ... and the whole is simply a chain too (as opposed to a net).

[aran]

Further to my earlier post, on the pigeon-matrix v base/cover approaches :
The pigeon-matrix approach requires the columns to be lined up so that all (bar one) are wis (weak inference set) ie no necessary truth or equivalently at most one truth, which then - to square with the total number of starting sis (or truths) - forces the remaining column (wherever it is, Steve K placing it conveniently first) to be an sis (strong inference set) ie must have at least one truth and hence the strength of the structure.
Having to line up the columns as wis being a possible drawback to easy execution.
One way to present the base/cover approach drawing on Steve K's format would be :

Code: Select all

base  cover        total new cover
5r7  5b5 r7c6            2       
5c3  r4c3                1
1c3  1b1 r4c3 r9c3       2       
1r3  1b1 r3c6            1
2c3  r5c3 r9c3           1
9c3  9b1 r4c3 r5c3       1   
9r3  9b1 r3c6            0

total : 7                8
rank : 8-7=1
elimination :
5r3c6 removes 5r7c6, r4c3=>rank reduced to 6
ie 7 truths in base to start with, reduced to 6 on same base : impossible : =><5>r3c6


Meaning of columns :
Column 1 : base sis listed
Column 2 : cover wis for the corresponding sis in Col 1.
Column 3 : total new cover sets in Col 2 (eg line 4 : 1 -not 2- because 1b1 has already occurred in line 3)
Total count of base sets/cover sets, giving rank and hence determining the nature of the "work" to be done.

Is the base/cover approach stronger ?
At first sight, the matrix "restricts" consideration to the sis column, whereas the base/approach determines a rank, then says : go find anything which reduces the rank to -1, appearing to give wider scope.

[aran]

... and the whole is simply a chain too (as opposed to a net).

...there are only chains, and chains are of interest when their endpoints can be usefully confronted.
A net so-called is a chain that has branched.
Those branches subsequently and necessarily converge within the chain.
Call that a net (as shorthand for a chain with a net) : not as opposed to a chain, but as opposed to a chain without a net
In your case, you have an sis of 3.
Three chains emerge and converge on <5>r3c6.
And that looks awfully like a branching operation.
I think it's a fine move, I just don't think it's a net-less chain.

[ronk]

The r3c6<>5 deduction can be "linearized" too:

r3c6 -5- r7c6 =5= r7c2 -5- r8c3 -7- r12c3 =7= r3c12 -7- als:r3c489 -5- r3c6 ==> r3c6<>5

(5)r7c6 = (5)r7c2 - (5=7)r8c3 - (7)r12c3 = (7)r3c12 - (7=5)als:r3c489 ==> r3c6<>5

[edit: r7c6 was typo r7c5]