AHH! I wish I would have posted before Steve K because this thread looks so much more enticing when Steve K is shown as the last poster, no?
nah, i rather see steves post anywhere usually he brings alot of inresting stuff to the table and creates a huge stir of events or views of his move in many diffrent fashions.
very nice find steve
and thanks for the alternative views on the moves everyone.
{thanks a solution view norm!}
but what other paths could we take.
after all the fancy stuff the beast still lives.
shes taking a good beating but still not down and out yet.
where to go from here?
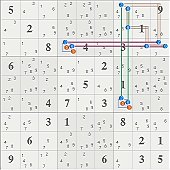
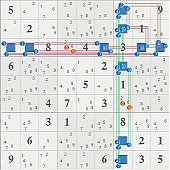
the grid as it is minus the first two move
followed by reduction by ss:}
- Code: Select all
.-----------------.------------------.-------------------.
| 5 34 167 | 238 23678 178 | 2467 478 9 |
| 34 2 679 | 5 3678 789 | 467 1 478 |
| 17 179 8 | 26 4 179 | 3 5 26 |
:-----------------+------------------+-------------------:
| 6 13789 179 | 489 18 2 | 5 478 3478 |
| 378 3789 2 | 4689 5 48 | 1 4678 34678 |
| 18 5 4 | 7 168 3 | 26 9 28 |
:-----------------+------------------+-------------------:
| 2 47 3 | 1 9 5 | 8 467 467 |
| 478 6 5 | 348 378 478 | 9 2 1 |
| 9 1478 17 | 248 278 6 | 47 3 5 |
'-----------------'------------------'-------------------'