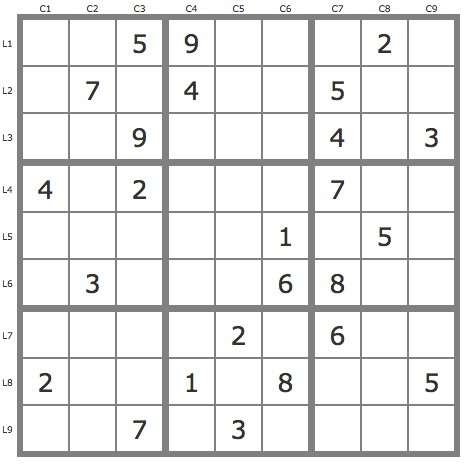
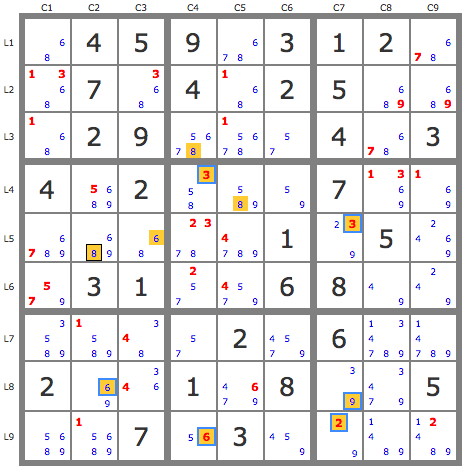
Hi Robert,
Mauriès Robert wrote:For this puzzle, the path I followed for both colors is as follows:
Yellow : 8r5c2=>6r5c3=>589r4c256=>3r4c4
Blue : 69r5c2=>589r4c256=>3r4c4
That's valid implication chain (or forcing chain) notation, and I'm sure we all can understand that. It shows the logic clearly, so it's definitely an improvement. It's also easy to convert into an AIC, and I'll show how shortly. I would suggest just a couple of minor tweaks first. Here's how I'd write it as a forcing chain:
8r5c2 -> 6r5c3 -> 589r4c256 -> 3r4c4
69r58c2 -> 589r4c256 -> 3r4c4
=> +3 r4c4; stte
One minor change is that '->' is used for the minor implications and '=>' for the final conclusion. It makes the latter easier to read, and it's important to show so we can more easily see what you wanted to prove. I also added spaces between the nodes for readability. Last but not least, I switched your 69r5c2 into a locked set in two cells 69r58c2 because that's how you probably intended it to work but it's not shown.
Furthermore, if you write 69 we interpret that to be a shorthand for 6&9, i.e. 6 AND 9. Obviously 6 and 9 can't both be true in one cell, so the correct interpretation is 6 OR 9, which we would write (6|9)r5c2. There's no real ambiguity with a single cell, but it's still preferable that way. I know it caused me a bit of a headache when I first read your solutions because I naturally saw it as 6 AND 9 (which works for the two-cell locked set but not for a single cell).
How you write this with your writing convention ?
Like I said, we can all understand that previous notation, so don't take any pressure about using AICs until you feel comfortable with them. We're happy to help, however, if you want to learn. It's actually quite easy, especially if we add the negative implications to the forcing chain:
8r5c2 -> -8r5c3 -> 6r5c3 -> -6r4c2 -> 589r4c256 -> -58r4c4 -> 3r4c4
69r58c2 -> -6r4c2 -> 589r4c256 -> -58r4c4 -> 3r4c4
Now we can just turn the implications into weak and strong inferences which must be alternating in an AIC (alternating inference chain). The first thing to notice is that your starting nodes are strongly linked (together they form an almost locked set, if we use my little change). Horizontally that's notated with the '=', but since we keep the two chains in two lines at first, we'll use '||' to denote a vertical strong link:
(8)r5c2 ...
||
(96)r58c2 ...
Note that I also added parentheses around the digits because it's standard Eureka (and I find it more readable). Some prefer not to use them and that's fine too. They're mandatory if we use internal linking within a term, as in: (8=96)r58c2. I also reordered the digits 69 -> 96 for readability because our next linking digit is the 6. Just a nuance, but I prefer it like that. So, let's then add the rest. Since the links must be alternating, the next links are weak, and after that strong again, and so on:
(8)r5c2 - (8=6)r5c3 - (6=958)r4c256
- (5|8=3)r4c4||
(96)r58c2 - (6=958)r4c256
- (5|8=3)r4c4=> +3 r4c4; stte
That's actually an AIC, just written on two lines. If you "pull" it straight into a single line, it's a normal AIC. It proves that one or the other end must be 3r4c4, so it must be true and can be placed. However, it has a bit of redundancy, and we prefer things as simple as possible. We don't in fact need to prove a placement as long as we prove an elimination that leads to it. So, if we cut out the last term from both ends (colored red) and straighten it out, we have this:
(589=6)r4c256 - (6=8)r5c3 -
(8)r5c2 = (96)r58c2 - (6=958)r4c256 => -58 r4c4, stte
One last tweak is to combine the colored (blue) nodes into a single ALS term:
(589=6)r4c562 - (6=8)r5c3 - (8=96)r58c2 - (6=958)r4c256 => -58 r4c4, stte
That's it. As you can see, it's almost the same as
eleven's chain, and the relevant logic is exactly the same. Mine is almost the same as well, except that I used the hidden pair (16)r4c89 to prove -3r4c8. Both lead to the same placement +3r4c4 which solves the puzzle.
Did that help? Btw, if you really want to conclude with a placement, you can add that cell to the ALS at both ends as eleven suggested:
(3=5896)r4c4562 - (6=8)r5c3 - (8=96)r58c2 - (6958=3)r4c2564 => +3 r4c4, stte
For the name of the section I propose, without pretension, Robert's puzzles.
Seems good to me!