by HATMAN » Mon Feb 12, 2024 7:53 am
by HATMAN » Mon Feb 12, 2024 7:53 am
Having eventually solved them neither is actually that difficult, I would put them on the 1.1 - 1.3 range on the assassin scale.
1 WT Rain KiMo 8B
Zero is present in every row, column and nonet.
Each other number is missing from exactly one row, column and nonet (it has been proven that the nonet is fixed at the crossover of the row and column).
W-T added definitions for Rainbow, as we need a short form to identify the missing numbers, so:
Row 1 missing number is R1m
Column 1 missing number is C1m
Nonet 1 missing number is N1m (I will also use this for Triankles and similar for the repeats there)
1. Nonet Sums
These puzzles are deliberately arranged around nonets.
45 Rule on each nonet:
N1 r2c2+N1m = 10(2)
N2m = 8, N3m = 7, N4m = 6, N5m = 1
N6: R5C8 + N6m = 9(2)
N7m = 5, N8m = 2, N9m = 4
These numbers will be missing from the relevant rows and columns.
Clean up the partners numbers in each two-cage.
2. Fix known cage totals
_8(2) is 8(2), _9(2) is 9(2), _0(2) is 10(2)
_5(9) = 45(9), no 0 in centre spots
Because of the zero there are less than standard KiMo
3. Solve N1 and N6 missing
Remaining missing are:
N16m = {39}
N1m+r2c2 = [91/37]
N6m+r5c8 = [90/36] but R5c8 <> 0
So r2c2 = 1, N1m = 9, r5c8 = 6 N6m = 3
Clean up
N1: r12c3 = 7(2)
N6: 18 locked in 8(2)&10(2)
Note: R123m = {789}, R456m = {136}, R789m = {245}, C123m = {569}, C456m = {128}, C789m = {347}
4. Derive cage totals by simple nonet arithmetic first
N16 done so:
N3: _9(3) = 9(3)
N7: _2(3) = 12(3)
4. Remove KiMo cage candidates
_2(2) <>16, _4(2) <>27, _6(2) <> 38
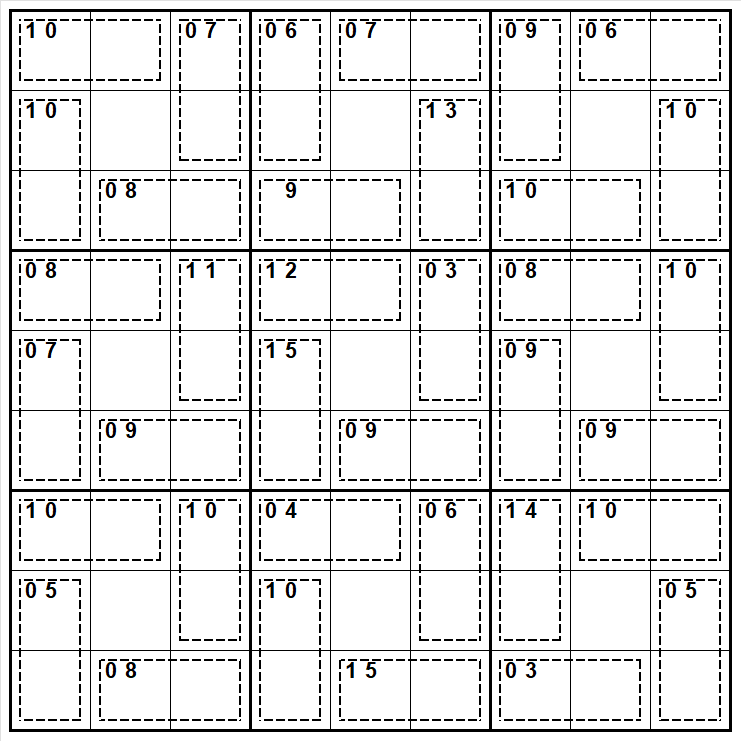
At this stage all the basics are done saved as Rainbow KiMo 8B s1.jsd.
5 Rows and columns
R3: 5 locked in 8(2), 9(2) r3c45 <>36
R6: set of 9(2) pairs missing from 1/3/6 -something here not sure what?
C9: r167 C9m =20(4) / 10(4) but r45c9 = {19/28} so not 10(4) -> r89c9 = 5(2) = {05/23}
->_3(2) at r9c78 <>{03}
N9: 05,12, 37, 689 / 05, [67], 19, 238 / 05, [67], 28, 139 / 23 19, 58, {06}7 / 23, 19, [67], 058
Consider C9 if r89 = 23 then r45 = {19} but r7c89 = {19} so r89c9 = {05} clean up
N9: 05,12, 37, 689 / 05, [67], 19, 238 / 05, [67], 28, 139 so_3(3) <>7
N3: 2*10(2) is two from 19/28/46 -> 9(2) <>18
C9m = 347 -> 6 locked in r123 so 10(2) = 64 or 9(3) = {03/12}6
R123c7<>6, r123c8r1c9<>4
But r3c78 = 19/28 so 9(3) <>126
N3: 46, 09, 28, 135 / 036, 45, 19/28
C8m = 4
R7: 0 locked in c456
N8: _3(3) <>012 r7c6<>6
Rainbow KiMo 8B s2.jsd.
C9: 8 locked in 10(2)*2 r7 ->r7c9<>2 (probably not much use but I like it)
N7: 08, {2+19/37/46} and 2*{19/37/46} / 039, 2*46/28, 17 / 048, 2*19/37, 26
N1: 05 locked in 7(2), 8(2) so 07, 35, 28/46 / 08, 25, 37/46 46 not in r123c3r3c2
N4: 89, 014, 35, 27 / 89, 023, 17, 45 / 07, 35, 18, 249 / 25, 08, fail 9(2)
/ 25, 09, 17, 348 / 25 078, fail 9(2) / 34, 08, 27, 159 / 34, 09, 17, 258 / 34, 078 fail 9(2)
N4: 89, 014, 35, 27 / 89, 023, 17, 45 / 07, 35, 18, 249 / 25, 09, 17, 348 / 34, 08, 27, 159 / 34, 09, 17, 258 ->_5(3)<>7
Rainbow KiMo 8B s3.jsd.
R4: _2(2) <>57 clash 2*8(2),
R4&N5: _2(2) <>{39} as c36={45} and 9(2), _5(2)<>6 so no 6 in N5
This is a WoW! moment: _2(2) = {02/28} 2*8(2)<>{08} -> r4c78 = {17}, r4c12 = {35}
Easy from here
28 locked in R4c459 R4m = 6, r4c36 ={9,0/4}
N6: r45c9= {28} 2*9(2) = 09/45, r23c9<>28 ->r3c78 = {28}
R3: R3c23 = {35} -> r3c45 = {09} -> R3m = 7
N1: r23c1 = {46}, r12c3 = {07}, R1c12 = {28} -> R1m=9, R2m = 7
N4: 89, 014, 35, 27 / 07, 35, 18, 249
N6&R6: r6c789 from 0459 ->2*9(2) <>0459, R6c23 = [72/81], R6c56 = {27/36}
Cannot be 18&36 as R6m =1/3 27 locked -> r6 c14 = {6/8&0/5/9} as 4 not in c1-6, r56c7<>[45]
Rainbow KiMo 8B s4.jsd.
C2: r9=0 HS, r9c2 = 8, 2*10(2)<>28
R7: c1289 = 19/37 clear r78c3 ={46}, C2m = 6, r5c2 = 4 HS, r45c3 = [92]
Fill some naked singles
Rainbow KiMo 8B s5.jsd.
R56c4 = 15(2) = [96], r4c45 =1292) = {48}, r4c6 =0, r5c6 =3
The rest is NS, HS and fixing cage totals.
[size=150]2 WT Rain KiMo 8
I expected the same breakthrough to work so this walkthrough is targeted at getting there early.
1. Nonet Sums
These puzzles are deliberately arranged around nonets.
45 Rule on each nonet:
N1 N1m = 9
N2m = 8, N3m = 7, N4m = 6, N5m = 1
N7m = 5, N8m = 2, N9m = 4
N6: R5C8 + N6m = 9(2) but only 3 un-missing -> N6m=3, R5c8 = 6
These numbers will be missing from the relevant rows and columns.
Clean up the partners numbers in each two-cage.
2. Fix known cage totals
_8(2) is 8(2), _9(2) is 9(2), _0(2) is 10(2)
_5(9) = 45(9), no 0 in centre spots
Because of the zero there are less than standard KiMo
N6: 18 locked in 8(2)&10(2)
Note: R123m = {789}, R456m = {136}, R789m = {245}, C123m = {569}, C456m = {128}, C789m = {347}
3. Derive cage totals by simple nonet arithmetic first
N6 done so:
N1: _8(3) = 8(3)
N3: _9(3) = 9(3)
N7: _2(3) = 12(3)
4. Remove KiMo cage candidates
_2(2) <>16, _4(2) <>27, _6(2) <> 38
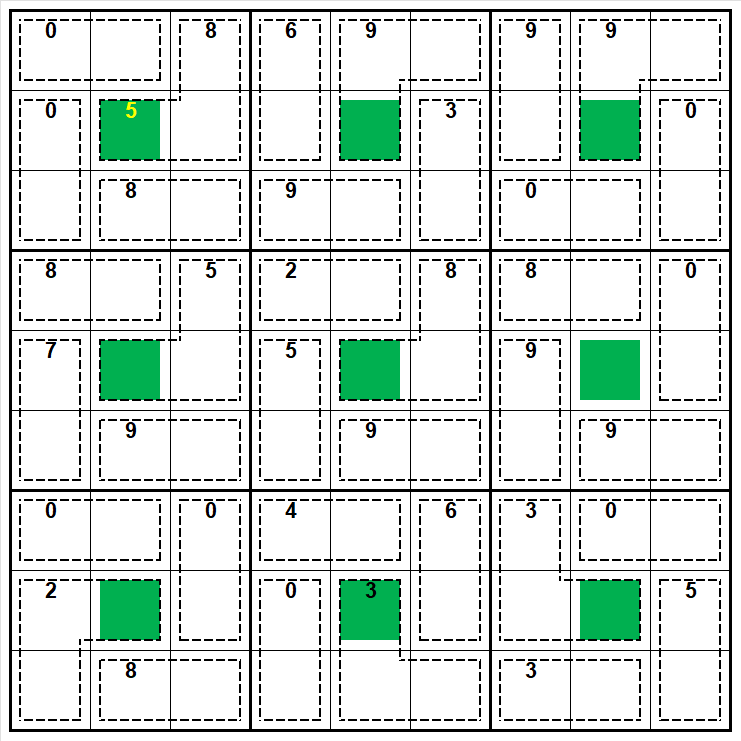
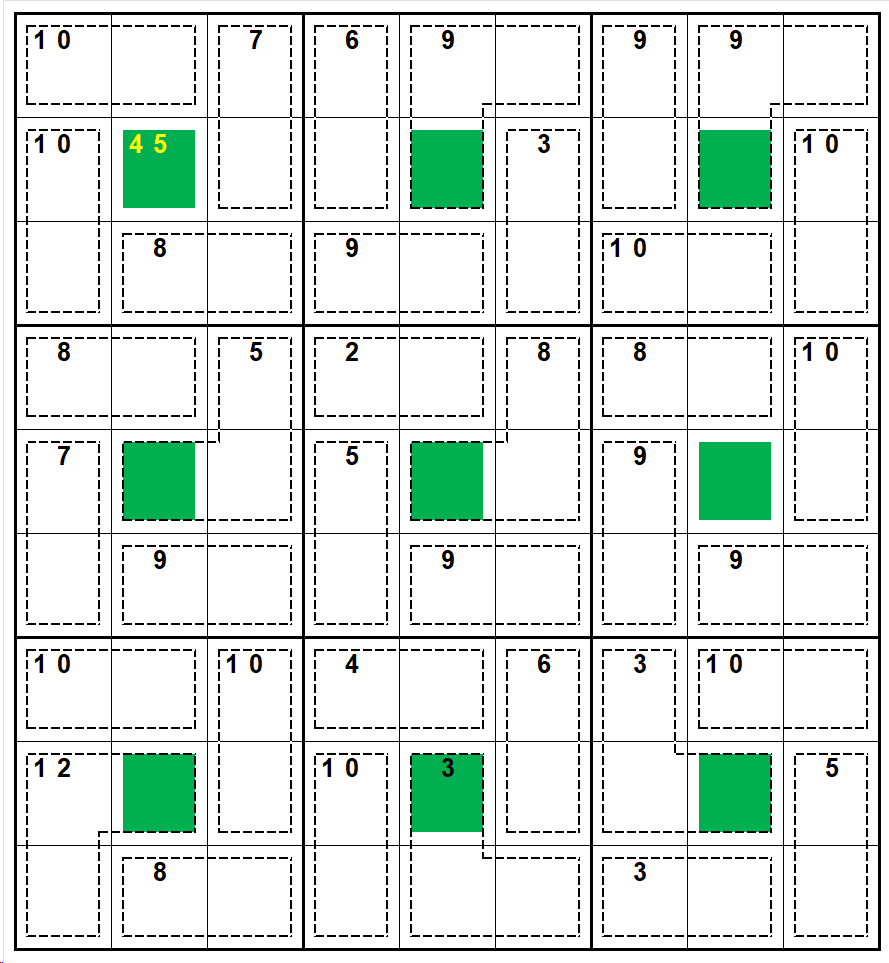
At this stage all the basics are done saved as Rainbow KiMo 8 s1.jsd.
R4: _2(2) <>57 conflict 2*8(2), if {39} r56c4&r6c56<>6, r1278 ={08/17} -> R4m = 6 -> r4c6<>6 so no 6 in N5 fail, _2(20 = {02/48} -> r12&r78 <> {08} -> r4c78 = {17} -> r4c12 = {35}
saved as Rainbow KiMo 8 s2.jsd.
Innies C9 r167 C9m =20(4) / 10(4) but 7 locked -> 20(40) -> r89c9 = 5(2) = {05}
N9: 05,12, 37, 689 / 05, [67], 19, 238 so_3(3) <>17
R3: 5 locked in 8(2), 9(2) r3c45 <>36
N7: 1 in C1 locked in N7 8(2)<>17, 26 clashes with _3(2) at r9c78 ->r9c23 = {08}
R9: c56 = {14/69}, c78 = {12}/[67], R9m=2/4 1246 locked, r14 = {3,7/9},
N3: 2*10(2) is two from 19/28/46 -> 9(2) <>18
s3 now
N7: 19, 372, 46, 08 / 192, 37/46, 08, 2 locked in r8c12
N4: 78 locked in _7(2), 9(2)
C9m = 347 -> 6 locked in r123 so 10(2) = 64 or 9(3) = {03/12}6
R123c7<>6, r123c8r1c9<>4
But r3c78 = 19/28 so 9(3) <>126/018 ->r3c78 = {28}, C8m = 4
saved as Rainbow KiMo 8 s3.jsd
N2; 0 of R3 locked in c456 so 09, 15/24, 67, 3-15/24 / 03, 45, 79, 126
R8c2 = 0 HS c2, r12c3 = 0x -> r56c1 = {07} -< r6c23 = [81]
R6m = 3, R5m = 1, r6c56 = {27}, r56c1 = [70], r6c89 = [54], r56c7 = [09], r56c4 = [96]
R4c45 = {48}, r4c3 = 9, r4c6 = 0, r3c45 = [09], r12c4 = 6(2)
R12c7 = {45}, r23c9 = {19}, r1c9 = 6 r12c8 = [03], r23c1 = {46}, r5c56 = [53] from 45(9)
The rest is NS, HS and fixing cage totals.[/size]