The New Sudoku Players' Forum

[Mauriès Robert]

I translate this into:

Code: Select all

1) choose a candidate A from a bivalue cell.
2) if T&E(BRT or S, 1, A) finds an error, then eliminate A
3) otherwise:
3a) either give up and goto 1)
3b) or go one level of T&E deeper, possibly iterating (which includes possibly going still deeper in T&E).


No criterion is given for choosing between 3a and 3b.
No criterion is given for choosing between the Zi's.

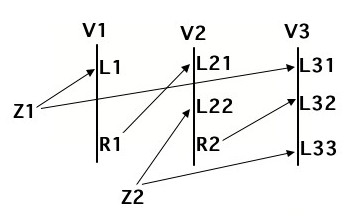
Misinterpretation (translation) of what I wrote.
Point 2) means that the construction sequence of the anti-track P'(E) has highlighted a candidate Z who sees both E and a candidate B of P'(E). This candidate B is the last candidate on the right of the sequence, i.e. the anti-track is no longer developed beyond it. It has nothing to do with T&E which develops the sequence until it finds an incompatibility.
Point 3b, consists in better defining the target if point 2) has not given anything at the end of a certain "reasonable" development of the anti-track. We do this by eliminating one of the Zi in addition to A and we continue as in 2) or 3b).
Reasonable here means that one imposes on oneself a number of candidates (from the right) not to be exceeded, because the goal is not to do T&E. Personally I give myself a limit of 10 candidates (from the right) and without result at this stage I come back to 3a).
The choice of the Zi to be eliminated is made so that the construction sequence continues with the objective of arriving at a candidate B who sees the target.
It should be noted that a too low limit obliges to a greater number of application of this procedure, and by hand this is more tedious and even inefficient because the goal is not like Sudorules to seek the simplest resolution.
While waiting to give you the complete resolution of the "fish-on-wave 9.3" puzzle you are asking me for, here is an example of elimination to better explain my procedure.
To simplify my work, I only give you the puzzle with the anti-track marking as I practice it by hand and some explanations.
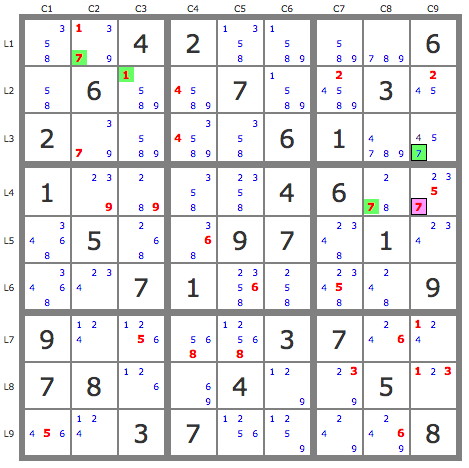
I treat a first elimination of "fish-on-wave 9.3".
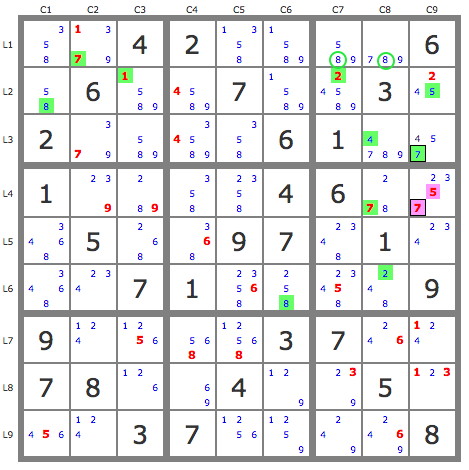
I choose E=7r4c9 (purple) and I trace P'(E) which is limited to 4 candidates (green), which gives no result. But the Zi are 235r4c9 and the target is thus among these three candidates.

puzzle1: Show

It is clear that by eliminating also the 5r4c9, so with E=57r4C9, I can develop P'(E) by the 5r2C9, which I do and this leads to the 2r6c8 which sees the 2r4c9 that I eliminate.

puzzle2: Show

The sequence that leads to this elimination is finally written (using the memory effect), three candidates (7r1c2, 1r2c3 and 7r4c8) were not taken into account because they did not contribute to the result.:
P'(E) : (-57r4c9) =>[7r3c9 and 5r2c9->8r2c1]->2r2c7->4r3c8->8r1c78->8r6c6->2r6c8 => -2r4c9.
Compare with the first whip [8] of your resolution.
Robert

[denis_berthier]

I wasn't asking you to try to reproduce my first whip. I was asking you to apply your method to this puzzle.

It is obvious that, by applying your method, your first elimination has no chance of being n2r4c9. (In the same way, a manual solver using whips could not apply the simplest first strategy and would have no chance of finding this elimination first.)
There are indeed 58 bivalue candidates that could be used for a start.

As for my first whip,

Code: Select all

whip[8]: c9n7{r4 r3} - c9n5{r3 r2} - r2n2{c9 c7} - b3n4{r2c7 r3c8} - r6c8{n4 n8} - c7n8{r6 r1} - c6n8{r1 r2} - r2c1{n8 .} ==> r4c9 ≠ 2


the comparison with your method is quite easy.
The initial resolution state is:

Code: Select all

   358       1379      4         2         1358      1589      589       789       6         
   58        6         1589      4589      7         1589      24589     3         245       
   2         379       589       34589     358       6         1         4789      457       
   1         239       289       358       2358      4         6         278       2357     
   3468      5         268       368       9         7         2348      1         234       
   3468      234       7         1         23568     258       23458     248       9         
   9         124       1256      568       12568     3         7         246       124       
   7         8         126       69        4         129       239       5         123       
   456       124       3         7         1256      1259      249       2469      8         


c9n7{r4 r3} is bivalue and therefore (exceptionally writing the target first) n2r4c9 - c9n7{r4 r3} is an obvious partial-whip[1]. The next two steps c9n5{r3 r2} and r2n2{c9 c7} are bivalue also. Notice that, up to this point, there might still be 3 targets: n2r4c9, n3r4c9, n5r4c9
The next two steps b3n4{r2c7 r3c8} and r6c8{n4 n8} are bivalue modulo the target n2r4c9. Only the next two steps c6n8{r1 r2} and r2c1{n8 .} involve t-candidates.

I choose E=7r4c9 (purple) and I trace P'(E) which is limited to 4 candidates (green), which gives no result. But the Zi are 235r4c9 and the target is thus among these three candidates.

Your procedure provides no reason for choosing this, if not trying to reproduce my first whip.

It is clear that by eliminating also the 5r4c9...

When something is not clear, start your sentence with "it is clear that".
Once more, the only thing that is clear is, your method provides no reason for choosing n5r4c9 instead of n2r4c9 or n3r4c9.

P'(E) : (-57r4c9) =>[7r3c9 and 5r2c9->8r2c1]->2r2c7->4r3c8->8r1c78->8r6c6->2r6c8 => -2r4c9

In this presentation, the logic behind the elimination is totally illegible.

[Mauriès Robert]

I wasn't asking you to try to reproduce my first whip. I was asking you to apply your method to this puzzle.
It is obvious that, by applying your method, your first elimination has no chance of being n2r4c9. (In the same way, a manual solver using whips could not apply the simplest first strategy and would have no chance of finding this elimination first.)
There are indeed 58 bivalue candidates that could be used for a start.

Among all pairs of candidates (bivalve candidates), some are more interesting than others. This is the case of 7b6 and 5b6 who have a cell in common, it is the case of 1b1 and 7b1 as well. I am therefore interested first in these pairs. Another criterion of choice for me too is that one of the two candidates of the pair allow the sequence to start.
Obviously, this guarantees nothing until the procedure I have described has been completed. It is the same for Sudorules, which goes through all the whip-partials [n-1] to find a whip [n].

I choose E=7r4c9 (purple) and I trace P'(E) which is limited to 4 candidates (green), which gives no result. But the Zi are 235r4c9 and the target is thus among these three candidates.

Your procedure provides no reason for choosing this, if not trying to reproduce my first whip.

You misinterpret my intentions. I explained to you previously why I am interested in pairs 5b6 and 7b6, therefore in the r4c9 cell common to both pairs, and in the 7r4c9 candidate for which the anti-track can be launched with 4 candidates.

It is clear that by eliminating also the 5r4c9...

When something is not clear, start your sentence with "it is clear that".
Once more, the only thing that is clear is, your method provides no reason for choosing n5r4c9 instead of n2r4c9 or n3r4c9.

I return the compliment, when we don't make the effort to understand we play on words ...
So I explain myself again ..:
The choice of 7r4c9 allows us to say that Z is among the 3 candidates 235r4c9. The choice of 5r2c9 allows to prolong the construction of the anti-track and to say that the target Z is then the 5r4c9, and thus to continue my procedure.

P'(E) : (-57r4c9) =>[7r3c9 and 5r2c9->8r2c1]->2r2c7->4r3c8->8r1c78->8r6c6->2r6c8 => -2r4c9

In this presentation, the logic behind the elimination is totally illegible.

Ok for the symbolism of the writing, we have already talked about it, I only indicate the candidates on the right of the sequence.
But for the logic of elimination this is clear: a candidate who sees both the generator of the anti-track and a candidate of the anti-track can be eliminated. This is the second theorem in my paper on TDP.
Robert

[denis_berthier]

Among all pairs of candidates (bivalve candidates), some are more interesting than others. This is the case of 7b6 and 5b6 who have a cell in common, it is the case of 1b1 and 7b1 as well

There are 25 bivalue candidates that "have a cell in common".

Another criterion of choice for me too is that one of the two candidates of the pair allow the sequence to start.
Obviously, this guarantees nothing until the procedure I have described has been completed. It is the same for Sudorules, which goes through all the whip-partials [n-1] to find a whip [n].

In short, you have no more criterion to start than me. You have been questioning me about how to start whips; but I see you have no more reasons than me to start form a candidate than from another.
SudoRules uses a whip[n] as soon as it is available; it doesn't have to scan all the partial-whips[n-1].

[Mauriès Robert]

Among all pairs of candidates (bivalve candidates), some are more interesting than others. This is the case of 7b6 and 5b6 who have a cell in common, it is the case of 1b1 and 7b1 as well

There are 25 bivalue candidates that "have a cell in common".

But only a few meet the second criterion.

Another criterion of choice for me too is that one of the two candidates of the pair allow the sequence to start.
Obviously, this guarantees nothing until the procedure I have described has been completed. It is the same for Sudorules, which goes through all the whip-partials [n-1] to find a whip [n].

In short, you have no more criterion to start than me. You have been questioning me about how to start whips; but I see you have no more reasons than me to start form a candidate than from another.
SudoRules uses a whip[n] as soon as it is available; it doesn't have to scan all the partial-whips[n-1].

I have never said that my approach with anti-tracks offered more possibilities than yours with whips or braids. I simply told you, in this thread in particular, that your resolutions with whips and braids could also be made with anti-tracks, namely that for each whip or braid one can find a set E such that target Z sees both an E and a candidate of anti-track P'(E).
Robert

[denis_berthier]

I have never said that my approach with anti-tracks offered more possibilities than yours with whips or braids.

You have strongly suggested that you had more reasons to choose a starting point.

I simply told you, in this thread in particular, that your resolutions with whips and braids could also be made with anti-tracks, namely that for each whip or braid one can find a set E such that target Z sees both an E and a candidate of anti-track P'(E).

The opposite is totally obvious for braids; anti-tracks are an awkward way of expressing the final contradiction of a braid.
But your assertion is false, as your anti-tracks have no z-candidates

[Mauriès Robert]

I simply told you, in this thread in particular, that your resolutions with whips and braids could also be made with anti-tracks, namely that for each whip or braid one can find a set E such that target Z sees both an E and a candidate of anti-track P'(E).

The opposite is totally obvious for braids; anti-tracks are an awkward way of expressing the final contradiction of a braid.
But your assertion is false, as your anti-tracks have no z-candidates

I maintain my assertion that your resolutions with whips and braids could also be made with an anti-track, i.e. for each whip or braid one can find a set E such that target Z sees both an E and an candidate of anti-tracking P'(E).
I don't see how an anti-track would be a clumsy way to do anything. The anti-track is defined without ambiguity, as is the theorem that states the condition of elimination.
Furthermore, what is your definition of a target?
Robert

[denis_berthier]

I simply told you, in this thread in particular, that your resolutions with whips and braids could also be made with anti-tracks, namely that for each whip or braid one can find a set E such that target Z sees both an E and a candidate of anti-track P'(E).

The opposite is totally obvious for braids; anti-tracks are an awkward way of expressing the final contradiction of a braid.
But your assertion is false, as your anti-tracks have no z-candidates

I maintain my assertion that your resolutions with whips and braids could also be made with an anti-track, i.e. for each whip or braid one can find a set E such that target Z sees both an E and an candidate of anti-tracking P'(E).

Robert, there's one thing you should understand: maintaining an assertion is not an argument. I've given you a very precise reason why it's not true. If you have any rational argument, then provide it; otherwise, there's no point in continuing this conversation.

[Mauriès Robert]

Robert, there's one thing you should understand: maintaining an assertion is not an argument. I've given you a very precise reason why it's not true. If you have any rational argument, then provide it; otherwise, there's no point in continuing this conversation.

Ok, I suggest you show this on the puzzle Fish on wave 9.3, or another one of your choice solved with braids or whips.

[denis_berthier]

Robert, there's one thing you should understand: maintaining an assertion is not an argument. I've given you a very precise reason why it's not true. If you have any rational argument, then provide it; otherwise, there's no point in continuing this conversation.

Ok, I suggest you show this on the puzzle Fish on wave 9.3, or another one of your choice solved with braids or whips.

This answer is totally absurd. Indeed, it only shows that you can't prove your assertion.

Even if an example or any number of examples satisfied it, it wouldn't prove it.
I don't have to show anything. You made an assertion, prove it (if you can).

[Mauriès Robert]

Hi Denis,
You misunderstand the meaning of my statement. I am not claiming that the elimination of a candidate with a braid or whip is necessarily with the procedure I have described using an anti-track. What I meant was that for all the examples of resolution I know of with braids or whips and which I have dealt with , I have achieved the same eliminations with my procedure. Admittedly this does not prove anything, but it is enough for me to ask myself whether this form of equivalence can be demonstrated. In the absence of a demonstration that I am unable to make, a counter-example of resolution would suffice to definitively rule out this question, a counter-example that I have not yet found.
As an example of my assertion, here is your resolution (braid) of Fish on wave 9.3 with my procedure, where you will note for each braid or whip there exists E of which P'(E) eliminates Z.
Robert

resolution: Show

E=56r7c3, -E => 5r9c1->6r8c3->9r8c4->12r89c6->1r1c5->1r2c3 => -1r7c3
E=57r4c9, -E => [ 7r3c9 and 5r2c9->8r2c1 ]->2r2c7->4r3c8->8r1c78->8r6c6->2r6c8 => -2r4c9.
E={5r7c3,1r2c3}, -E => [ 5r9c1 & ( 1r1c2->1r2c6->1r9c5 )->7r1c8 ]->6r9c8->9r3c8->9r2c3 => -5r2c3
E={8r2c1,8r75c4}, -E => 5r2c1->( 75r34c9 & 5r7c3 )->6r7c4->3r5c4->3r6c7->5r4c9->8r4c4 => -8r2c4
E={1r2c3,8r4c3}, -E => 1r1c2->7r3c2->( 7r1c8 & 9r4c2 )->2r4c3->( 8r4c8 & 2r6c56 )->4r6c8->9r3c8->9r2c3 => -8r2c3
E=1r2c3, -E => [ ( 1r8c3->6r8c4 ) & ( 1r1c2->7r1c8->7r4c9->5r6c7->3r5c79 ) ]->8r5c4->5r7c4->5r9c1->6r9c8->9r3c8->9r2c4 => -9r2c3 => r2c3=1
E=9r8c4, -E => [ 9r23c4 & ( 6r8c4 ->2r8c3->2r5c79->26r79c8->9r89c7 ) ]->9r2c4 => -9r3c4
E={5r9c1,6r6c1,6r9c8}, -E => ( 5r7c3 & 6r7c8 & 6r6c5 )->8r7c4->3r5c4->5r4c4->5r6c7->3r4c9->7r3c9->5r2c29->8r2c1->9r2c6->9r8c4->6r8c3 => -6r9c1 => -6r5c3
E=9r8c4, -E => 6r8c4->[ ( 2r8c3->6r7c3->5r3c3 & 6r6c5 ) & ( 9r2c4->24r2c79) ]->5r4c9->5r6c6->2r9c6 => -9r9c6 => -9r8c7
E={2r2c9,3r5c9}, -E => 2r2c7->3r8c7->3r4c9->7r3c9->5r2c9->4r3c8->( 8r2c1 & 8r1c78)->8r6c6->2r6c8 => -2r5c9
E=2r5c3, -E => 2r5c7->26r79c8->9r9c7->4r7c9->4r5c1->5r9c1->26r78c3 => -2r4c3
E=57r4c9, -E => 7r3c9->5r2c9->2r2c7->( 4r3c8 & 2r5c3->6r8c3->5r7c3->4r9c1)->4r7c9->3r5c9 => -3r4c9
E={6r8c3,9r8c4}, -E->( 9r2c4 & 6r7c3->5r3c3->8r2c1)->5r2c6->5r1c7->5r6c5->6r5c4 => -6r8c4 => r8c4=9, r8c3=6
E=2r8c6, -E => [( 1r8c6->1r9c2) & ( 23r8c79->2r46c8->2r5c3 ) ]->2r7c2 => -2r7c5
E=4r9c1, -E => 5r9c1->2r7c3->2r5c7->2r9c8->9r9c7 => -4r9c78 => -4r7c2
E=6r6c1, -E => 6r5c1->6r7c4->8r7c5->5r7c3->4r9c1 => -4r6c1
E=3r5c9, -E => 4r5c9->( 4r9c1 & 4r2c7->5r2c4)->5r1c1->5r6c7 => -3r6c7 => -3r5c14
E=6r6c1, -E => 6r5c1->( 4r6c2 & 6r6c5 )->3r6c1 => -8r6c1
E=24r5c7, -E => 2r5c3->5r7c3->4r9c1->4r5c9->3r5c7 => -8r5c7
E=1r1c5, -E => 1r1c6->9r2c6->8r6c6->6r5c4->6r6c1->3r1c1 => -3r1c5 => -3r3c2
E=-9r2c6, -E => [ ( 9r2c7->2r9c7->2r5c3 )->2r7c2->1r9c2 ]->5r9c6 => -5r2c6
E={3r1c1,7r1c2}, -E => ( 7r1c8 & 3r6c1->6r6c5->6r9c8 )->9r3c8->9r1c2 => -3r1c2 => r1c1=3, r6c1=6, r5c4=6, r4c4=9
E=4r56c7, -E => 4r2c7->5r2c4->8r2c1->4r5c1 => -4r5c9 => r5c9=3, r8c7=3
E={5r3c3,5r19c5}, -E => 5r7c3->5r9c6->5r1c7->5r6c5 => -5r3c5
E=2r2c9, -E => 2r2c7->2r5c3->5r7c3->5r2c1 => -5r2c9 => -4r3c9
E=3r4c4, -E => 3r3c4->8r3c5->8r7c4 => -8r4c4
E=8r3c3, -E => 5r3c3->5r4c9->7r4c8->8r4c5 => -8r3c5 => r3c5=3, stte.

[denis_berthier]

Admittedly this does not prove anything, but it is enough for me to ask myself whether this form of equivalence can be demonstrated.

There are two major obstructions for a general proof:
- you have no z-candidates (the E' substitute is a priori weaker)
- your require a link between the target and the last candidate.
This is enough for me for not wanting to spend time on your conjecture.

for all the examples of resolution I know of with braids or whips and which I have dealt with , I have achieved the same eliminations with my procedure.
[...]
E=56r7c3, -E => 5r9c1->6r8c3->9r8c4->12r89c6->1r1c5->1r2c3 => -1r7c3

Taking the first line of your resolution, I see that you use some Subset[2]: 12r89c6. So, in this case, you introduce some compensation for the missing power related to my two objections.

[Mauriès Robert]

Hi Denis,

There are two major obstructions for a general proof:
- you have no z-candidates (the E' substitute is a priori weaker)
- ...

I don't understand what you're explaining to me ??

E=56r7c3, -E => 5r9c1->6r8c3->9r8c4->12r89c6->1r1c5->1r2c3 => -1r7c3
Taking the first line of your resolution, I see that you use some Subset[2]: 12r89c6. So, in this case, you introduce some compensation for the missing power related to my two objections.

Normal, with TDP the sequences are constructed using basic techniques, therefore closed sets.
Robert

[Mauriès Robert]

Hi Denis,
Could you give me an example of bi-whip [n] or bi-braid [n] for n>1. It would help me to understand this notion better.
If not, does the graph below represent a bi-whip[3]?


Robert

[denis_berthier]

There are two major obstructions for a general proof:
- you have no z-candidates (the E' substitute is a priori weaker)
- ...

I don't understand what you're explaining to me ??

If you don't understand my answer about z-candidates, how do you want to understand anything about bi-whips?
Your graphics, copied from [BUM] (with Z2 added), can represent a particular biwhip[3].