- Code: Select all
. . . . . . . 5 .
4 . . . . 7 3 . .
. . 5 2 . . . . 1
7 . . . . 3 . . .
. . . . 7 . 8 . .
. . 6 1 . . . 9 .
3 . . . 6 . 4 . .
. . 1 . . . . . 5
. 5 . 9 . . . 3 .
.......5.4....73....52....17....3.......7.8....61...9.3...6.4....1.....5.5.9...3.
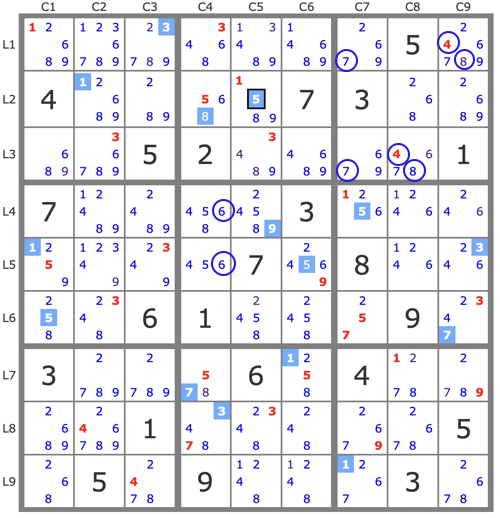
12689 1236789 23789 3468 13489 14689 2679 5 246789
4 12689 289 568 1589 7 3 268 2689
689 36789 5 2 3489 4689 679 4678 1
7 12489 2489 4568 24589 3 1256 1246 246
1259 12349 2349 456 7 24569 8 1246 2346
258 2348 6 1 2458 2458 257 9 2347
3 2789 2789 578 6 1258 4 1278 2789
2689 246789 1 3478 2348 248 2679 2678 5
268 5 2478 9 1248 1248 1267 3 2678
Puzzle 28
5 posts
• Page 1 of 1
Puzzle 28
not an easy puzzle, at least for me; its simplest path is long enough: 55 chains with a maximum length of 5 + a few basic patterns; the shortest path i found is 4 chains with a maximum length of 9; but i find it interesting in that it first resolution state has no bivalue cells.
- P.O.
- Posts: 2121
- Joined: 07 June 2021
Re: Puzzle 28
Hi P.O.,
The puzzle does not have a bivalue cell in rc, but does in rn and cn, for example 5r2c45.
The following (TDP) track (where "->" indicates the order of construction) shows that 5r2c5 can be eliminated, while 5r2c4 is a simple backdoor.
P(5r2c5) : [ 5r2c5->1r2c2->1r5c1->( 5r6c1->5r4c7->1r9c7->1r7c6 )->5r5c6->6r45C4 ]->8r2c4->48b3->7r13c7->7r6c9->3r5c9->3r1c3->3r8c4->7r7c4->... => 5r7 empty => r2c5≠5 => r2c4=5, stte.
It is also possible to solve with a set of two tracks, the interactions are enough to find the solution without finding contradiction as before, like this:
P(5r2c5) : [ 5r2c5->1r2c2->1r5c1->( 5r6c1->5r4c7->1r9c7->1r7c6 )->5r5c6->6r45C4 ]->8r2c4->48b3->7r13c7->7r6c9->...
P(5r2c4) : 5r2c4->5r7c6->1r7c8->1r4c7->5r6c7->7r6c9->...
=> r6c9=7, stte
Robert
The puzzle does not have a bivalue cell in rc, but does in rn and cn, for example 5r2c45.
The following (TDP) track (where "->" indicates the order of construction) shows that 5r2c5 can be eliminated, while 5r2c4 is a simple backdoor.
P(5r2c5) : [ 5r2c5->1r2c2->1r5c1->( 5r6c1->5r4c7->1r9c7->1r7c6 )->5r5c6->6r45C4 ]->8r2c4->48b3->7r13c7->7r6c9->3r5c9->3r1c3->3r8c4->7r7c4->... => 5r7 empty => r2c5≠5 => r2c4=5, stte.
puzzle1: Show
It is also possible to solve with a set of two tracks, the interactions are enough to find the solution without finding contradiction as before, like this:
P(5r2c5) : [ 5r2c5->1r2c2->1r5c1->( 5r6c1->5r4c7->1r9c7->1r7c6 )->5r5c6->6r45C4 ]->8r2c4->48b3->7r13c7->7r6c9->...
P(5r2c4) : 5r2c4->5r7c6->1r7c8->1r4c7->5r6c7->7r6c9->...
=> r6c9=7, stte
puzzle2: Show
Robert
Last edited by Mauriès Robert on Tue Mar 22, 2022 1:16 pm, edited 4 times in total.
- Mauriès Robert
- Posts: 619
- Joined: 07 November 2019
- Location: France
Re: Puzzle 28
hi Robert, thank you for your solution; i am familiar with the Extended Sudoku Board representation of the four 2D spaces as introduced by Denis in his book HLS and also i read this thread: http://forum.enjoysudoku.com/the-bivalue-conjecture-t38764.html
at the start of this puzzle i counted 24 such 'extended' bivalue cells:
i also checked for backdoors and antibackdoors, and found:
15 1-AntiBackdoors. all after Singles (S)
at the start of this puzzle i counted 24 such 'extended' bivalue cells:
Hidden Text: Show
15 1-AntiBackdoors. all after Singles (S)
- Code: Select all
((((1 4 2) (3 4 6 8)) 3 S) (((2 2 1) (1 2 6 8 9)) 1 S) (((2 5 2) (1 5 8 9)) 5 S) (((3 2 1) (3 6 7 8 9)) 3 S) (((4 7 6) (1 2 5 6)) 5 S) (((5 1 4) (1 2 5 9)) 1 S) (((5 3 4) (2 3 4 9)) 3 S) (((6 1 4) (2 5 8)) 5 S) (((6 7 6) (2 5 7)) 7 S) (((6 9 6) (2 3 4 7)) 3 S) (((7 4 8) (5 7 8)) 5 S) (((7 6 8) (1 2 5 8)) 1 S) (((8 4 8) (3 4 7 8)) 7 S) (((8 5 8) (2 3 4 8)) 3 S) (((9 7 9) (1 2 6 7)) 1 S))
- Code: Select all
((((1 1 1) (1 2 6 8 9)) 1 S) (((1 3 1) (2 3 7 8 9)) 3 S) (((1 4 2) (3 4 6 8)) 4 S) (((1 9 3) (2 4 6 7 8 9)) 6 Z) (((2 2 1) (1 2 6 8 9)) 6 S) (((2 4 2) (5 6 8)) 5 S) (((2 5 2) (1 5 8 9)) 1 S) (((3 2 1) (3 6 7 8 9)) 8 S) (((3 5 2) (3 4 8 9)) 3 S) (((3 7 3) (6 7 9)) 7 S) (((4 5 5) (2 4 5 8 9)) 5 S) (((4 7 6) (1 2 5 6)) 1 S) (((4 9 6) (2 4 6)) 4 Z) (((5 1 4) (1 2 5 9)) 5 S) (((5 2 4) (1 2 3 4 9)) 1 S) (((5 3 4) (2 3 4 9)) 4 S) (((5 9 6) (2 3 4 6)) 3 S) (((6 1 4) (2 5 8)) 8 S) (((6 2 4) (2 3 4 8)) 3 S) (((6 7 6) (2 5 7)) 5 S) (((6 9 6) (2 3 4 7)) 7 S) (((7 4 8) (5 7 8)) 7 S) (((7 6 8) (1 2 5 8)) 5 S) (((7 8 9) (1 2 7 8)) 1 S) (((8 4 8) (3 4 7 8)) 3 S) (((8 5 8) (2 3 4 8)) 8 S) (((8 8 9) (2 6 7 8)) 7 S) (((9 6 8) (1 2 4 8)) 1 S) (((9 7 9) (1 2 6 7)) 6 S))
- P.O.
- Posts: 2121
- Joined: 07 June 2021
Re: Puzzle 28
here is my solution:
- Code: Select all
c-12689 1236789 23789 3468 13489 14689 2679 5 246789
4 b+12689 289 a±568 a1+589 7 3 268 2689
689 36789 5 2 3489 4689 679 4678 1
7 12489 2489 e4-×568 24589 3 e12+56 1246 246
c+1259 12349 2349 d4*×56 7 d24*569 8 1246 2346
258 2348 6 1 2458 2458 257 9 2347
3 2789 2789 h+578 6 g+1258 4 g-1278 2789
2689 246789 1 3478 2348 248 2679 2678 5
268 5 2478 9 1248 1248 f+1267 3 2678
r2n5{c4 c5} - r2n1{c5 c2} - c1n1{r1 r5} - r5n5{c1 c4c6} - r4n5{c4 c7} - c7n1{r4 r9} - r7n1{c8 c6} - r7n5{c6 c4} => r4c4 r5c4 <> 5
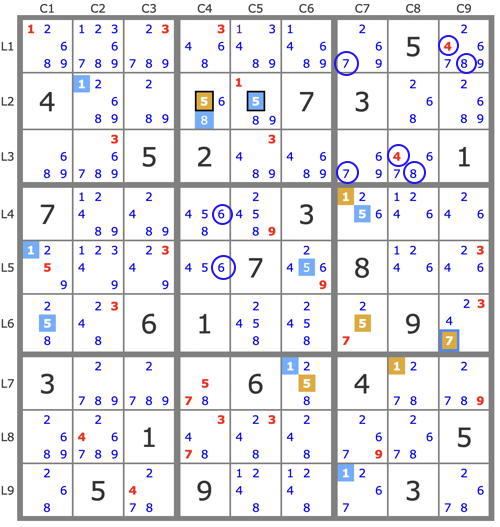
12689 1236789 23789 g+3468 13489 14689 2679 5 246×789
4 12689 289 568 1589 7 3 268 2689
689 h+36789 5 2 h-3489 4689 i6*79 i46*78 1
7 12489 2489 468 24589 3 b12+56 1246 246
1259 12349 2349 46 7 24569 8 1246 2346
258 2348 6 1 2458 2458 a25+7 9 a234±7
3 2789 2789 e+578 6 d+1258 4 d-1278 2789
2689 246789 1 f347+8 2348 248 2679 2678 5
268 5 2478 9 1248 1248 c+1267 3 2678
r6n7{c9 c7} - c7n5{r6 r4} - c7n1{r4 r9} - r7n1{c8 c6} - r7n5{c6 c4} - c4n7{r7 r8} - c4n3{r8 r1} - r3n3{c5 c2} - r3n7{c2 c7c8} => r1c9 <> 7
12689 1236789 d2-3789 c+3468 13489 14689 2679 5 h2+4689
4 12689 289 a±56×8 1589 7 3 i26*8 i26*89
689 36789 5 2 3489 4689 679 g46+78 1
7 12489 2489 468 24589 3 1256 1246 246
1259 12349 d2+349 46 7 24569 8 1246 e2-346
258 2348 6 1 2458 2458 257 9 e2+347
3 2789 2789 a+578 6 1258 4 g12-78 f2*789
2689 246789 1 b34+78 2348 248 2679 g26-78 5
268 5 2478 9 1248 1248 1267 3 f26*78
c4n5{r2 r7} - c4n7{r7 r8} - c4n3{r8 r1} - c3n3{r1 r5} - c9n3{r5 r6} - c9n7{r6 r7r9} - c8n7{r7r8 r3} - b3n4{r3c8 r1c9} - b3n8{r1c9 r2c8r2c9} => r2c4 <> 8
c-12689 1236789 23789 3468 13489 14689 2679 5 24689
4 b+12689 289 a±5×6 a1+589 7 3 268 2689
689 36789 5 2 3489 4689 679 4678 1
7 12489 2489 e4*68 24589 3 1256 1246 246
c+1259 12349 2349 e4*6 7 d24+569 8 1246 2346
258 2348 6 1 2458 2458 257 9 2347
3 2789 2789 578 6 1258 4 1278 2789
2689 246789 1 3478 2348 248 2679 2678 5
268 5 2478 9 1248 1248 1267 3 2678
r2n5{c4 c5} - r2n1{c5 c2} - c1n1{r1 r5} - r5n5{c1 c6} - b5n6{r5c6 r4c4r5c4} => r2c4 <> 6
ste.
- P.O.
- Posts: 2121
- Joined: 07 June 2021
Re: Puzzle 28
Two AIC steps:
1. (374)r6c279 = r6c56 - r45c4 = (43-7)r18c4 = (75-1)r7c46 = r7c8 - r9c7 = (1-5)r4c7 = (537)r6c279 loop
=>-2 r6c279, -8 r6c2, -4 r4c5, r5c6, -6 r1c4, -8 r18c4, r7c46, -2 r7c6, -26r4c7
2. (5)r2c4 = (5-1)r2c5 = r2c2 - r1c1 = (1-5)r5c1 = r6c1 - (5=7)r6c7 - (7=2698)b3p1567 => -8 r2c4; ste
- Code: Select all
+----------------------------+-------------------------+-------------------------+
| 12689 1236789 23789 | d34-68 13489 14689 | 2679 5 246789 |
| 4 12689 289 | 568 1589 7 | 3 268 2689 |
| 689 36789 5 | 2 3489 4689 | 679 4678 1 |
+----------------------------+-------------------------+-------------------------+
| 7 12489 2489 | c4568 2589-4 3 | h15-26 1246 246 |
| 1259 12349 2349 | c456 7 2569-4 | 8 1246 2346 |
| 258 ia34-28 6 | 1 b2458 b2458 |ia57-2 9 ia347-2 |
+----------------------------+-------------------------+-------------------------+
| 3 2789 2789 | e57-8 6 e15-28 | 4 f1278 2789 |
| 2689 246789 1 | d347-8 2348 248 | 2679 2678 5 |
| 268 5 2478 | 9 1248 1248 | g1267 3 2678 |
+----------------------------+-------------------------+-------------------------+
1. (374)r6c279 = r6c56 - r45c4 = (43-7)r18c4 = (75-1)r7c46 = r7c8 - r9c7 = (1-5)r4c7 = (537)r6c279 loop
=>-2 r6c279, -8 r6c2, -4 r4c5, r5c6, -6 r1c4, -8 r18c4, r7c46, -2 r7c6, -26r4c7
- Code: Select all
+----------------------------+-------------------------+-------------------------+
| d12689 1236789 23789 | 34 13489 14689 | h2679 5 246789 |
| 4 c12689 289 | a56-8 b1589 7 | 3 h268 h2689 |
| 689 36789 5 | 2 3489 4689 | h679 4678 1 |
+----------------------------+-------------------------+-------------------------+
| 7 12489 2489 | 4568 2589 3 | 15 1246 246 |
| e1259 12349 2349 | 456 7 2569 | 8 1246 2346 |
| f258 34 6 | 1 2458 2458 | g57 9 347 |
+----------------------------+-------------------------+-------------------------+
| 3 2789 2789 | 57 6 15 | 4 1278 2789 |
| 2689 246789 1 | 347 2348 248 | 2679 2678 5 |
| 268 5 2478 | 9 1248 1248 | 1267 3 2678 |
+----------------------------+-------------------------+-------------------------+
2. (5)r2c4 = (5-1)r2c5 = r2c2 - r1c1 = (1-5)r5c1 = r6c1 - (5=7)r6c7 - (7=2698)b3p1567 => -8 r2c4; ste
Cenoman
- Cenoman
- Posts: 3211
- Joined: 21 November 2016
- Location: France
5 posts
• Page 1 of 1