The New Sudoku Players' Forum

[mith]

Code: Select all

+-------+-------+-------+
| 7 . 1 | . 3 . | . . 9 |
| . 8 . | 7 . 6 | . . . |
| . . 3 | . 5 . | 7 . . |
+-------+-------+-------+
| . . . | 4 . 2 | . 9 . |
| . . . | . 7 . | 1 . 5 |
| . . . | . . 5 | . 8 . |
+-------+-------+-------+
| 1 . . | 5 . . | . . . |
| . 2 . | . . . | . . 4 |
| 9 . 5 | . . . | . 6 . |
+-------+-------+-------+
7.1.3...9.8.7.6.....3.5.7.....4.2.9.....7.1.5.....5.8.1..5......2......49.5....6.

The goal is not to solve, just to place one digit. (Though I'm sure Cenoman will have a one-stepper for us in no time. ) There's a neat trick here that I hadn't seen before.

[denis_berthier]

SER = 9.1, W = 10,
4 backdoors: n8r7c6, n2r3c4, n2r1c8, n8r1c4
6 W1-backdoors: the same four + n5r2c8, n2r2c1

It's remarkable there isn't a single placement until the end

Code: Select all

***********************************************************************************************
***  SudoRules 20.1.s based on CSP-Rules 2.1.s, config = W+SFin
***  Using CLIPS 6.32-r770
***********************************************************************************************
213 candidates, 1349 csp-links and 1349 links. Density = 5.97%
whip[1]: c8n7{r8 .} ==> r9c9 ≠ 7, r7c9 ≠ 7
hidden-pairs-in-a-block: b3{r1c7 r3c9}{n6 n8} ==> r3c9 ≠ 2, r3c9 ≠ 1, r1c7 ≠ 5, r1c7 ≠ 4, r1c7 ≠ 2
biv-chain[3]: r4c7{n3 n6} - r1n6{c7 c2} - c2n5{r1 r4} ==> r4c2 ≠ 3
t-whip-rn[3]: r5n2{c3 c8} - r1n2{c8 c4} - r3n2{c4 .} ==> r6c1 ≠ 2
biv-chain[4]: r4c7{n3 n6} - r1n6{c7 c2} - r1n5{c2 c8} - b9n5{r8c8 r8c7} ==> r8c7 ≠ 3
biv-chain[5]: r4c7{n3 n6} - r1n6{c7 c2} - r1n5{c2 c8} - b9n5{r8c8 r8c7} - b9n9{r8c7 r7c7} ==> r7c7 ≠ 3
t-whip[7]: r1n2{c4 c8} - r1n5{c8 c2} - r1n6{c2 c7} - r4c7{n6 n3} - r5c8{n3 n4} - c7n4{r6 r2} - r2c1{n4 .} ==> r2c5 ≠ 2
whip[1]: c5n2{r9 .} ==> r9c4 ≠ 2
whip[6]: r1n6{c7 c2} - c2n5{r1 r4} - r4n1{c2 c5} - r6c5{n1 n9} - r2c5{n9 n4} - c7n4{r2 .} ==> r6c7 ≠ 6
whip[7]: c7n4{r6 r2} - c3n4{r2 r7} - c5n4{r7 r9} - b8n2{r9c5 r7c5} - r7n6{c5 c2} - b1n6{r1c2 r3c1} - c1n4{r3 .} ==> r6c2 ≠ 4
whip[9]: r5n6{c3 c4} - r6n6{c5 c9} - c9n7{r6 r4} - r4c3{n7 n8} - r4c5{n8 n1} - r6c5{n1 n9} - r2c5{n9 n4} - r1c6{n4 n8} - r5n8{c6 .} ==> r4c2 ≠ 6
whip[9]: r5n6{c3 c4} - r6n6{c5 c9} - c9n7{r6 r4} - r4c3{n7 n8} - r4c5{n8 n1} - r6c5{n1 n9} - r2c5{n9 n4} - r1c6{n4 n8} - r5n8{c6 .} ==> r4c1 ≠ 6
whip[9]: c5n4{r9 r2} - c7n4{r2 r6} - c3n4{r6 r5} - b7n4{r7c3 r9c2} - r1n4{c2 c8} - r1n5{c8 c2} - r2c1{n5 n2} - b3n2{r2c9 r3c8} - r5n2{c8 .} ==> r7c6 ≠ 4
whip[8]: b7n8{r8c3 r7c3} - c9n8{r7 r3} - r1c7{n8 n6} - r4c7{n6 n3} - r9c7{n3 n2} - r7n2{c9 c5} - r7n4{c5 c2} - r7n6{c2 .} ==> r8c7 ≠ 8
whip[9]: b8n2{r7c5 r9c5} - c5n4{r9 r2} - r1c6{n4 n8} - r1c7{n8 n6} - r4c7{n6 n3} - r9c7{n3 n8} - r7n8{c9 c3} - r7n4{c3 c2} - r7n6{c2 .} ==> r7c5 ≠ 9
whip[10]: b8n2{r9c5 r7c5} - c5n4{r7 r2} - r1c6{n4 n8} - b3n8{r1c7 r3c9} - r7c9{n8 n3} - r9c9{n3 n2} - r7c8{n2 n7} - r7c6{n7 n9} - r7c7{n9 n8} - r9c7{n8 .} ==> r9c5 ≠ 1
whip[10]: r7n6{c3 c5} - b8n2{r7c5 r9c5} - b8n4{r9c5 r9c6} - r1c6{n4 n8} - r1c7{n8 n6} - r4c7{n6 n3} - r9c7{n3 n8} - r7n8{c7 c3} - r8c3{n8 n7} - r9n7{c2 .} ==> r8c1 ≠ 6
whip[10]: r4n5{c1 c2} - c2n1{r4 r6} - b5n1{r6c5 r4c5} - r4n8{c5 c3} - b4n7{r4c3 r6c3} - r8c3{n7 n6} - b7n8{r8c3 r8c1} - r8c5{n8 n9} - r6c5{n9 n6} - r7n6{c5 .} ==> r4c1 ≠ 3
whip[1]: r4n3{c9 .} ==> r5c8 ≠ 3, r6c7 ≠ 3, r6c9 ≠ 3
naked-pairs-in-a-block: b6{r5c8 r6c7}{n2 n4} ==> r6c9 ≠ 2
whip[6]: r5c8{n2 n4} - r3c8{n4 n1} - b2n1{r3c4 r2c5} - r4n1{c5 c2} - c2n5{r4 r1} - r1c8{n5 .} ==> r7c8 ≠ 2
whip[6]: r5c8{n2 n4} - r1c8{n4 n5} - c2n5{r1 r4} - r4n1{c2 c5} - r2n1{c5 c9} - r3c8{n1 .} ==> r2c8 ≠ 2
whip[6]: r5c8{n4 n2} - r1c8{n2 n5} - c2n5{r1 r4} - r4n1{c2 c5} - r2n1{c5 c9} - r3c8{n1 .} ==> r2c8 ≠ 4
whip-cn[9]: c6n1{r9 r3} - c8n1{r3 r2} - c9n1{r2 r9} - c4n1{r9 r6} - c2n1{r6 r4} - c2n5{r4 r1} - c8n5{r1 r8} - c8n3{r8 r7} - c8n7{r7 .} ==> r8c5 ≠ 1
whip[9]: b8n2{r9c5 r7c5} - c5n4{r7 r2} - r1c6{n4 n8} - c7n8{r1 r7} - r7c9{n8 n3} - c8n3{r8 r2} - r2n1{c8 c9} - c9n2{r2 r9} - r9c7{n2 .} ==> r9c5 ≠ 8
whip[6]: c7n8{r9 r1} - r1n6{c7 c2} - c2n5{r1 r4} - r4c1{n5 n8} - c5n8{r4 r8} - b7n8{r8c1 .} ==> r7c9 ≠ 8
whip[4]: b6n3{r4c7 r4c9} - r7c9{n3 n2} - c7n2{r7 r6} - c7n4{r6 .} ==> r2c7 ≠ 3
t-whip[6]: c9n8{r3 r9} - c9n1{r9 r2} - c9n2{r2 r7} - r9c7{n2 n3} - r9c4{n3 n1} - r3n1{c4 .} ==> r3c6 ≠ 8
t-whip[7]: b9n8{r9c9 r7c7} - r1c7{n8 n6} - r4c7{n6 n3} - r9c7{n3 n2} - c9n2{r9 r2} - r1n2{c8 c4} - r1n8{c4 .} ==> r9c6 ≠ 8
whip[7]: c1n8{r5 r8} - c5n8{r8 r7} - c5n2{r7 r9} - b8n4{r9c5 r9c6} - r9n7{c6 c2} - r8c3{n7 n6} - b8n6{r8c4 .} ==> r4c3 ≠ 8
naked-triplets-in-a-row: r4{c3 c7 c9}{n7 n6 n3} ==> r4c5 ≠ 6, r4c2 ≠ 7
whip[6]: r4c3{n7 n6} - r8c3{n6 n8} - r8c1{n8 n3} - r6c1{n3 n4} - c3n4{r5 r2} - c7n4{r2 .} ==> r7c3 ≠ 7
whip[9]: r5c8{n4 n2} - r1n2{c8 c4} - r3n2{c4 c1} - c1n4{r3 r2} - c3n4{r2 r7} - c5n4{r7 r9} - c5n2{r9 r7} - r7n6{c5 c2} - b1n6{r1c2 .} ==> r5c2 ≠ 4
whip[4]: r8c1{n3 n8} - c3n8{r8 r5} - r5n4{c3 c8} - r5n2{c8 .} ==> r5c1 ≠ 3
t-whip[10]: r4c5{n8 n1} - r6n1{c5 c2} - r4c2{n1 n5} - r4c1{n5 n8} - r8c1{n8 n3} - b4n3{r6c1 r5c2} - c2n9{r5 r3} - b2n9{r3c4 r2c5} - r6c5{n9 n6} - r8c5{n6 .} ==> r7c5 ≠ 8
whip[5]: c2n5{r1 r4} - r4n1{c2 c5} - c5n8{r4 r8} - b7n8{r8c1 r7c3} - b7n4{r7c3 .} ==> r1c2 ≠ 4
t-whip[4]: r1n4{c6 c8} - r5c8{n4 n2} - r3c8{n2 n1} - b2n1{r3c4 .} ==> r2c5 ≠ 4
whip[1]: c5n4{r9 .} ==> r9c6 ≠ 4
hidden-pairs-in-a-block: b8{r7c5 r9c5}{n2 n4} ==> r7c5 ≠ 6
whip[1]: b8n6{r8c5 .} ==> r8c3 ≠ 6
biv-chain[4]: c5n6{r8 r6} - r6c9{n6 n7} - r4n7{c9 c3} - r8c3{n7 n8} ==> r8c5 ≠ 8
hidden-single-in-a-column ==> r4c5 = 8
btte

[denis_berthier]

There's a neat trick here that I hadn't seen before.

Will you tell us the trick?

[Mauriès Robert]

Hi,
I don't know what mith wants. But here's a special approach.
In B1, 5r2c1 or 9r2c3 is necessarily a solution, just as 5r1c2 or 9r3c3 is necessarily a solution. Indeed,

(-5r2c1 and -9r2c3) => 24r2c13->(4r6c7 and 6r3c1->6r1c7->3r4c7)->2r5c8 => 2B3 empty, impossible

puzzle1: Show

(-5r1c2 and -9r3c3) => (46c2r13->37r79c2->68r8c13->6 and 5r4c2->1r4c5)->9r6c5 => r8c5 empty, impossible

puzzle2: Show

Therefore, 9r3c2 can be eliminated since, taking into account the previous result :
9r3c2->[5r2c1->5r4c2->(1r4c5 and 1r6c2) et 9r2c5]->6r6c5->(6r8c4 and 8r8c5)->7r8c4 => 7B4 empty, impossible.

puzzle3: Show

So 9r2c3 and 5r1c2 can be placed, which allows 10 other candidates to be placed with the basic techniques, which greatly simplifies the puzzle.

puzzle4: Show

Robert

[mith]

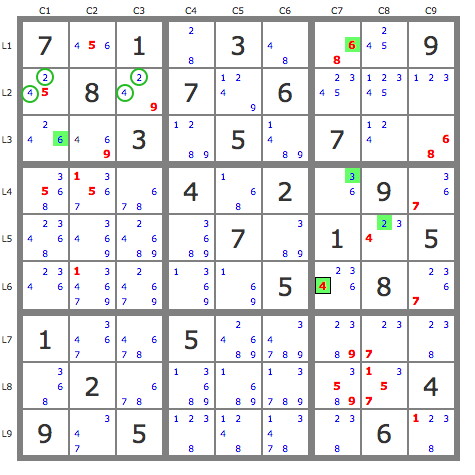
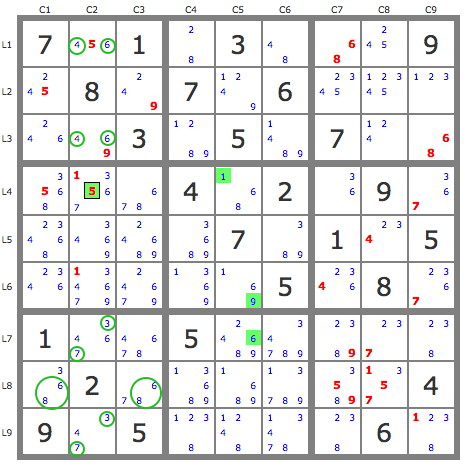
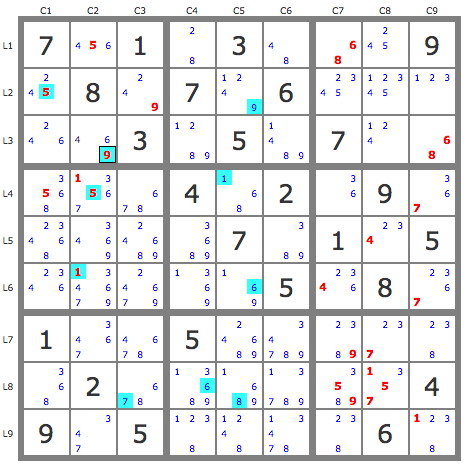
Consider the following partition - the cells sitting in odd numbered rows and columns are colored red (or purple, in box 9), and the cells sitting in even numbered rows and columns are colored blue. It's easy to show that the red/purple cells must contain the same digits as the blue cells, plus one additional set of 1-9. (Consider rows 13579, and columns 2468; the former is five sets of 1-9 containing red and purple cells, plus some other cells in the odd rows and even columns; the latter is four sets of 1-9 containing blue cells, plus the same other cells in even columns and odd rows. This sort of argument is equivalent to MSLS.)

Red cells: 13 odd digits, 8 empty
Purple cells: 4 empty
Blue cells: 6 even digits

Red/Purple must contain 10 even digits (6 + the extra set of 4)
But because of the 46 in box 9, Purple can only contain 2 even digits, so the other 8 must be in red.
Additionally, we can't have more even digits in Blue, so the remaining Blue cells are odd.

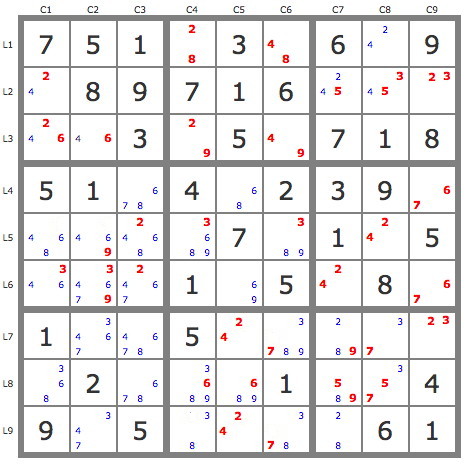
And now in column 4, we have a hidden single 6 - it can't go in the blue cells, and was already ruled out of the yellow squares. So +6r5c4, and the puzzle reduces all the way down to SER 8.5...

[mith]

Additionally, I've found the following general formula for this type of intersection argument.

Given the following partitions:

Split the 9 rows into sets of size R1 and R2.
Split the 9 columns into sets of size C1 and C2.
Split the 9 digits into sets of size D1 and D2.

Say R1xC1 contains X1 digits from R1. Likewise, R2xC2 contains X2 digits from R2.

Then, in the final solution, the following equality must hold:

X1 + X2 = (R1 * C1 * D1 + R2 * C2 * D2)/9

(If X1 + X2 is already equal to the right hand side in the current state of the puzzle, we can conclude what the remaining digits in the intersections must be.)

So for the specific case of odd digits in 25 red squares and even digits in 16 blue squares, we need 21 total digits to conclude that the remainder must be of the opposite parity. Here we had 19, thus the trick with box 9 to get the extra 2.

(The trick doesn't reduce the difficulty of this one that much, but I'm going to work on finding an example the reduces it to basics at least. The above puzzle is a modification of a puzzle by Sam Cappleman-Lynes, which does have 15 given odd digits in the red/purple cells.)

[Mauriès Robert]

Hi mith,

So +6r4c5, and the puzzle reduces all the way down to SER 8.5...

I think you wanted to write 6r5c4.
Robert

[denis_berthier]

Additionally, I've found the following general formula for this type of intersection argument.

Do you have an idea of:
1) how frequent such situations can be?
2) the computational complexity of finding such triplets of partitions?

[mith]

Hi mith,

So +6r4c5, and the puzzle reduces all the way down to SER 8.5...

I think you wanted to write 6r5c4.
Robert

Oops, fixed!

Denis, I can create them manually, but I haven't really started to approach it as a programming problem yet. As far as complutational complexity... the initial part should be no more complex than MSLS. If we are already at equality, there should always be a corresponding MSLS. (I think this should be the case even for cells which aren't filled but are restricted to the digit partition?)

If we're not at equality, there may be a lot we need to check. Here, we are checking the one box that has four empty red (now purple) cells, and seeing that there are already two even digits in that box. But in general, even a box with only two red cells could contribute (if both are empty and there are three even digits elsewhere in the box), and the same could be applied to rows or columns (though in this case there may be a better partition available, so I don't know how much checking this adds).

Of course, there's not necessarily a reason to restrict our partitions to rows and columns in the first place; I could imagine partitioning the above grid into the intersections of r13579/c135/b3 and r2468/c246/b69, for example - the given digits don't make this partition helpful, but for a different arrangement of digits it could be. Sort of a Mutant MSLS.

[Cenoman]

The trick doesn't reduce the difficulty of this one that much

Allow me not to agree. Without the 6r5c4 placement, the puzzle is not easy to solve (needs complex steps with multi-krakens... Forget the one-stepper that needs a plethora .
Things are not what they appear to be. The trick is a huge step, followed by a simple end:
1. +6r5c4:

Code: Select all

 +--------------------------+-------------------------+------------------------+
 |  7      456      1       |  28     3      a48      |  68     245     9      |
 |  245    8        249     |  7      1249    6       |  2345   12345   123    |
 |  246    469      3       |  1289   5       1489    |  7      124     68     |
 +--------------------------+-------------------------+------------------------+
 |  3568   13567    678     |  4      18      2       |  36     9       367    |
 |  2348   349      2489    |  6      7       389     |  1      234     5      |
 |  2346   134679   24679   |  139    19      5       |  2346   8       2367   |
 +--------------------------+-------------------------+------------------------+
 |  1      3467     4678    |  5      24689   34789   |  2389   237     238    |
 |  368    2        678     |  1389   1689    13789   |  3589   1357    4      |
 |  9      347      5       |  1238   1248    13478   |  238    6       1238   |
 +--------------------------+-------------------------+------------------------+

2. (4=8)r1c6 - r5c6 = (8-1)r4c5 = (1-5)r4c2 = (5)r1c2 => -4 r1c2
3. (5)r1c2 = (5-1)r4c2 = r4c5 - (19=2|4)r26c5 - (248=6)r1c467 => -6 r1c2; 17 placements & basics
Very simple finish with an X-chain:

Hidden Text: Show

Code: Select all

 +----------------------+-------------------+-------------------+
 |  7     5      1      |  28    3    48    |  6     24    9    |
 |  24*   8      9      |  7     1    6     |  245*  35    23   |
 |  246   46     3      |  29    5    49    |  7     1     8    |
 +----------------------+-------------------+-------------------+
 |  5     1      67     |  4     8    2     |  3     9     67   |
 |  8-4   9      248    |  6     7    3     |  1     24*   5    |
 |  346   3467   2467   |  1     9    5     |  24*   8     67   |
 +----------------------+-------------------+-------------------+
 |  1     3467   4678   |  5     24   789   |  289   37    23   |
 |  38    2      78     |  389   6    1     |  589   357   4    |
 |  9     347    5      |  38    24   78    |  28    6     1    |
 +----------------------+-------------------+-------------------+

4. (4)r2c1 = r2c7 - r6c7 = r5c8 => -4 r5c1; basics to the end

This may not be true for each occurrence of the pattern, but for this example, it is clearly very helpful.

[mith]

"Much" is relative of course. It does reduce it out of the realm of dynamic chains (SE) and steps with similar complexity, it's certainly helpful. I'd like to find some examples that reduce further into more trivial realms (at least to a reasonable one-stepper, if not basics).

I'm pretty happy to have realized this would work, though, no question there.

[StrmCkr]

gonna mark this up as a guess as i cant prove it atm.

[mith]

You're not wrong, but I'm not seeing a simple way to demonstrate that?

[StrmCkr]

what i did note is that you could reduce the pm's of all the red and blue cells respectfully to your notes {of even in red} and odd in blue.

Code: Select all

.-------------------.-------------------.-------------------.
| 7     456   1     | 28    3     48    | 2468  245   9     |
| 245   8     249   | 7     1249  6     | 2345  135   123   |
| 246   469   3     | 1289  5     1489  | 7     124   268   |
:-------------------+-------------------+-------------------:
| 3568  1357  678   | 4     18    2     | 36    9     367   |
| 248   349   248   | 6     7     389   | 1     234   5     |
| 2346  1379  24679 | 139   19    5     | 2346  8     2367  |
:-------------------+-------------------+-------------------:
| 1     3467  468   | 5     2468  34789 | 2389  237   2378  |
| 368   2     678   | 139   1689  1379  | 3589  1357  4     |
| 9     347   5     | 1238  248   13478 | 238   6     12378 |
'-------------------'-------------------'-------------------'

[SpAce]

what i did note is that you could reduce the pm's of all the red and blue cells respectfully to your notes {of even in red} and odd in blue.

grid: Show

Code: Select all

.-------------------.-------------------.-------------------.
| 7     456   1     | 28    3     48    | 2468  245   9     |
| 245   8     249   | 7     1249  6     | 2345  135   123   |
| 246   469   3     | 1289  5     1489  | 7     124   268   |
:-------------------+-------------------+-------------------:
| 3568  1357  678   | 4     18    2     | 36    9     367   |
| 248   349   248   | 6     7     389   | 1     234   5     |
| 2346  1379  24679 | 139   19    5     | 2346  8     2367  |
:-------------------+-------------------+-------------------:
| 1     3467  468   | 5     2468  34789 | 2389  237   2378  |
| 368   2     678   | 139   1689  1379  | 3589  1357  4     |
| 9     347   5     | 1238  248   13478 | 238   6     12378 |
'-------------------'-------------------'-------------------'

I think you're right (but I could be wrong). You can get a few more eliminations by noting that 2 and 8 must go to the purple cells (+ taking basics, which you haven't). After basics (1 pp, 1 hp) and the placement of +6r5c4 we have:

Code: Select all

  R               R              R                R/P            R/P
         B                B              B               B
.-----------------------.-----------------------.---------------------.
| 7      456      1     | 28     3       48     | 68     245     9    |    R
| 245    8        249   | 7      1249    6      | 2345   135-24  123  | B
| 246    469      3     | 1289   5       1489   | 7      124     68   |    R
:-----------------------+-----------------------+---------------------:
| 3568   1357-6   678   | 4      18      2      | 36     9       367  | B
| 248-3  349      248-9 | 6      7       389    | 1      234     5    |    R
| 2346   1379-46  24679 | 139    19      5      | 2346   8       2367 | B
:-----------------------+-----------------------+---------------------:
| 1      3467     468-7 | 5      2468-9  34789  | 2389   37-2    238  |    R/P
| 368    2        678   | 139-8  1689    1379-8 | 359-8  1357    4    | B
| 9      347      5     | 1238   248-1   13478  | 238    6       1238 |    R/P
'-----------------------'-----------------------'---------------------'


14 eliminations:

-odds from red: -3 r5c1, -9 r5c3, -7 r7c3, -9 r7c5, -1 r9c5
-evens from blue: -24 r2c8, -6 r4c2, -46 r6c2, -8 r8c46
-28 from non-purple in box 9: -2 r7c8, -8 r8c7

resulting grid: Show

Code: Select all

.-------------------.-------------------.------------------.
| 7     456   1     | 28    3     48    | 68    245   9    |
| 245   8     249   | 7     1249  6     | 2345  135   123  |
| 246   469   3     | 1289  5     1489  | 7     124   68   |
:-------------------+-------------------+------------------:
| 3568  1357  678   | 4     18    2     | 36    9     367  |
| 248   349   248   | 6     7     389   | 1     234   5    |
| 2346  1379  24679 | 139   19    5     | 2346  8     2367 |
:-------------------+-------------------+------------------:
| 1     3467  468   | 5     2468  34789 | 2389  37    238  |
| 368   2     678   | 139   1689  1379  | 359   1357  4    |
| 9     347   5     | 1238  248   13478 | 238   6     1238 |
'-------------------'-------------------'------------------'

Do we all agree that those are valid eliminations based on the previous deductions about the partitions? (I'm far from confident about this type of logic.)

If so, then the rest is easy:

Code: Select all

.--------------------.-------------------.--------------------.
| 7     c456   1     | 28    3     48    | b68    d245   9    |
| 245    8     249   | 7     1249  6     |  2345   135   123  |
| 246    469   3     | 1289  5     1489  |  7     d124   68   |
:--------------------+-------------------+--------------------:
| 3568   1357  678   | 4     18    2     | a36     9     367  |
| 248    349   248   | 6     7     389   |  1     d24-3  5    |
| 2346   1379  24679 | 139   19    5     |  2346   8     2367 |
:--------------------+-------------------+--------------------:
| 1      3467  468   | 5     2468  34789 |  2389   37    238  |
| 368    2     678   | 139   1689  1379  |  359    1357  4    |
| 9      347   5     | 1238  248   13478 |  238    6     1238 |
'--------------------'-------------------'--------------------'

(3=6)r4c7 - r1c7 = (6-5)r1c2 = (524)r135c8 => -3 r5c8

Code: Select all

.------------------.------------.----------------.
|  7    5     1    | 28  3   48 |  6    c24   9  |
| a24   8     9    | 7   1   6  | b245   35   23 |
|  246  46    3    | 29  5   49 |  7     1    8  |
:------------------+------------+----------------:
|  5    1     67   | 4   8   2  |  3     9    67 |
|  8-4  9     248  | 6   7   3  |  1    d24   5  |
|  346  37    2467 | 1   9   5  |  24    8    67 |
:------------------+------------+----------------:
|  1    3467  46   | 5   24  89 |  89    37   23 |
|  38   2     78   | 39  6   1  |  59    357  4  |
|  9    34    5    | 38  24  7  |  28    6    1  |
'------------------'------------'----------------'

Kite: (4)r2c1 = r2c7 - r1c8 = (4)r5c8 => -4 r5c1; stte