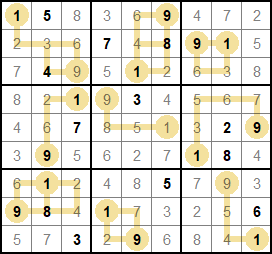
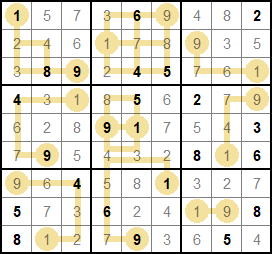
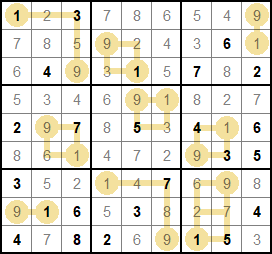
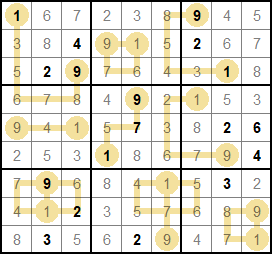
Hajime wrote:I don't understand 'ascending path'. You may omit clues?
Look at the first grid of the example's solution. You can go from 1 to 9 using two ascending paths: 1-2-3-4-9, 1-2-3-6-9
They go always in ascending order 1<2<3<4<9. I wouldn't be valid the path 1-2-7-
4-9, for example.
There should be always at least 1 path with those conditions on each grid. It may seem like not much of a restriction, but it can help eliminate many candidates.
creient wrote:Solution 1 is missing a possible path in box 7, bottom-left 1-2-4-8-9 is possible too.
Good sight. I'll fix it now.
creient wrote:How does your solver solve this?
I made my solver using Ruby, it checks for basic techniques (looks for singles, intersections, naked/hidden subsets, wings, etc) and for more complex cases it makes a guessing for each candidate.
It does its job except with very difficult puzzles, but it won't find 3D-Medusa or things like that

It doesn't do all at once, it's a step by step process like the Andrew Stuart's solver.
To make this variant I created a new Sudoku sub-class and applied the new restriction on the eliminate block/row/column intersections step, to eliminate extra candidates if possible.
I used a simplified version of A* Pathfinding to get all possible paths.
Probably this won't help much but I'll post here the piece of code that gets all the paths.
- Code: Select all
# Custom restriction of box/column/row pointing: Pathfinding
def iterate_bcr_path
for dbox in 0...9 # For each 3x3 box
next if @solved_boxes.include?(dbox)
c = self.cells.select{|x| x.box == dbox}
# Get cells with 1 as candidate
c1 = c.select{|cell| cell.values.include?(1)}
# Get cells with 9 as candidate
c9 = c.select{|cell| cell.values.include?(9)}
# We will only use those cases with both cells resolved
# On the guess candidates part this will automatically check those
# boxes that didn't have one of the candidates resolved yet
next if c1.size > 1 or c9.size > 1
# s = start cell (1), e = end cell (9)
s, e = c1[0], c9[0]
iterate_pathfinding(s, e)
end
end
# Iterate Pathfinding
def iterate_pathfinding(s, e)
# Get X, Y of the start and end cells
sx = self.cells.index(s) % 9
ex = self.cells.index(e) % 9
sy = (self.cells.index(s).to_f / 9).floor
ey = (self.cells.index(e).to_f / 9).floor
# If the distance between them is 2 or less every candidate is possible
# inbetween (1-n-9) so no candidates will never be eliminated
return if ((sx - ex).abs + (sy - ey).abs) <= 2
# Create initial path
paths = [Path_Route.new([[sx, sy]])]
# Get all possible paths
get_paths(paths, ex, ey)
# Select solved paths only
paths = paths.select{|path| path.solved}
# If no solved paths were found, the puzzle is broken
# That means that 1/9 candidate is not possible in that cell
if paths.size == 0
@broken_candidate = true
return
end
# Get all cells involved in any possible path
route_cells = []
for path in paths
for k in path.hash_route.keys
if !route_cells.include?(k) && path.hash_route[k] != 9
route_cells.push(k)
end
end
end
# Get all cells involved in EVERY possible path, remove non-used
# candidates of that cell
for i in route_cells
if paths.all?{|path| path.hash_route.keys.include?(i)}
values = []
for path in paths
values.push(path.hash_route[i])
end
values.uniq!
cell = get(*i)
next if cell.start
cell.values = values.clone
end
end
# Get those numbers that appear in EVERY possible path, remove them in
# non-involved cells
for i in 2..8
if paths.all?{|path| path.hash_route.values.include?(i)}
box = get(sx, sy).box
coords = []
for path in paths
coords.push(path.hash_route.invert[i])
end
coords.uniq!
coords_cells = coords.map{|x| get(*x)}
next i if coords_cells.any?{|cell| cell.box != box}
for c in self.cells.select{|cell| cell.box == box}
next if coords_cells.include?(c)
c.values.delete(i)
end
end
end
end
# Get all possible ascending paths
def get_paths(paths, ex, ey)
loop do
# Loop until all paths have no more steps
break if paths.all?{|path| path.end_route == true}
r = paths.select{|path| path.end_route == false}
for path in r # For each path
ix, iy = *path.current
# Get neighbors
n = [[ix, iy + 1], [ix - 1, iy], [ix + 1, iy], [ix, iy - 1]]
n = n.select{|x| x.all?{|v| v >= 0 && v <= 8}}
n = n.select{|x| !path.route.include?(x)}
for node in n # For each neighbor
cell = get(*node)
for value in cell.values
res = path.clone
# Include as new path if the neighbor has a greater value than
# the current cell
if value > path.value
res.value = value
res.route.push(node)
res.hash_route[node] = value
# If the neighbor's value is 9, the path ends automatically
if res.value == 9
res.end_route = true
res.solved = true if node == [ex, ey]
end
paths.push(res)
end
end
end
path.end_route = true
end
end
end