It is, of course, the "Einstein" hat. This 13-sided polygon, recently discovered by David Smith et al, is the very first aperiodic monotile ever discovered, solving an existence problem that has persisted for at least the past century.
When I'm not hunting for new 18-clue puzzles, I have been building some tools to explore the properties of these hats.
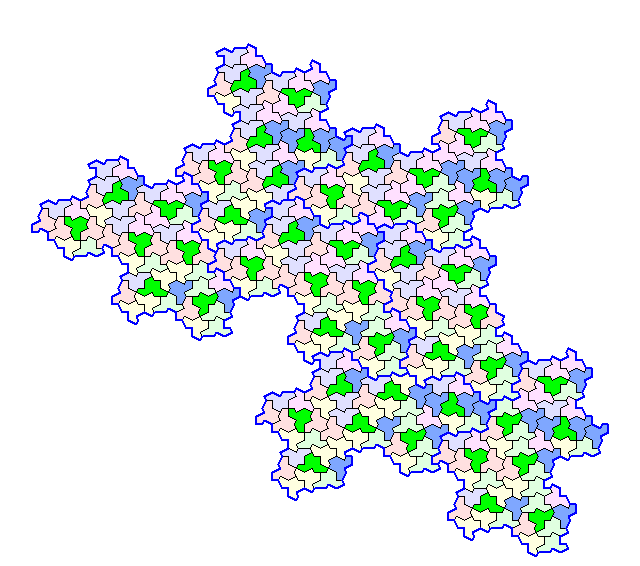
If you download the Smith paper (which you can access via reference [3] of the Wiki article linked above), you will find the background (Fig 2.11, p18) for my image below. It's a H7/H8 "super cluster", formed by combining clusters (patches of 7 or 8 hats).
The central hat for each cluster is coloured green. These are the only hats that have been "flipped" (reversed) - all the others are "normal", with a different colour used according to the hat's 6 possible orientations. So hats with the same colour all have the same orientation (other than the green hats).
The first-level clusters are outlined in blue. The super-cluster is formed by replacing each patch with a larger cluster (more or less!).
Each hat, by the way, consists of 8 identical "kites", which my avatar shows in different colours.