The New Sudoku Players' Forum

by **Mathimagics** » Tue Jul 05, 2022 2:32 pm

.
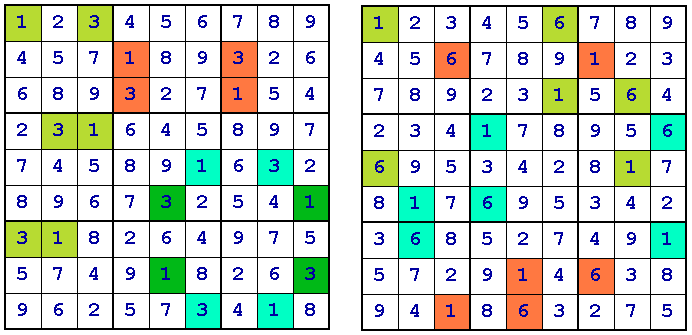
I have found an interesting sub-species of Sudoku grids, based on the cycle structure. The term "cycle" is described here, and the following examples should serve to illustrate the concept.

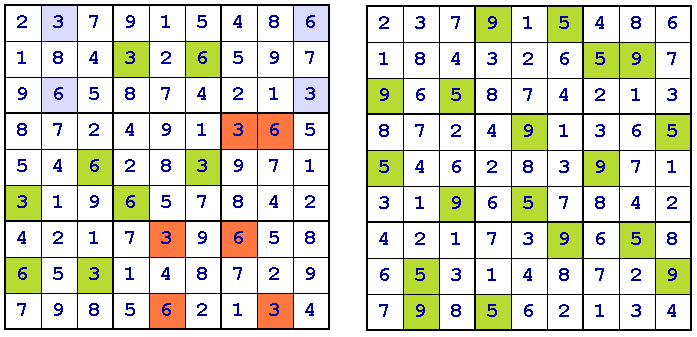
On the left we have the cycles for {AB} = {36}. There are 3 cycles, of lengths 2, 3 and 4.
On the right we have {AB} = {59}, for which there is a single cycle of length 9.

Some essential facts:

there are 36 digit pair {AB} possibilities

for each AB, there are from 1 to 4 cycles, and the lengths of these cycles will sum to 9

for any AB, there are 8 different combinations of cycle lengths
- 9
- 7 + 2, 6 + 3, 5 + 4
- 5 + 2 + 2, 4 + 3 + 2, 3 + 3 + 3
- 3 + 2 + 2 + 2

the total number of cycles (TNC) in any grid is thus in the range [36, 144]

A monocyclic grid is one which every AB pair has cycle length 9, and thus the grid has only 36 cycles in total. There are only 9 grids with this property. In this list they are tagged with band# and automorphism count (7 of the 9 are automorphic):

Code: Select all: 123456789456789123798231564275943618369815472841627395587362941612594837934178256 # 14 123456789456789123897231645231564978645978231978312564369147852582693417714825396 # 17 NA = 6 123456789456789123897231645231564978645978231978312564369825417582147396714693852 # 17 NA = 6 123456789456789231789123645231564897564897312897231456375618924618942573942375168 # 27 NA =36 123456789456789231789123645231564897564897312897231456375942168618375924942618573 # 27 NA =18 123456789456789231789123645231564897564897312978312564395248176617935428842671953 # 27 NA = 6 123456789456789231789123645231564897564897312978312564395671428617248953842935176 # 27 NA = 6 123456789456789231789123645231564978564897123897231564375942816618375492942618357 # 27 NA =36 123456789457289163698713254261847935579362841834591627315928476786134592942675318 # 354

There only 8 cases of "almost" monocyclic grids, these have 35 cycles of length 9, with one {AB} pair divided into 2 or 3 cycles, so TNC = 37 or 38:

Code: Select all: 123456789456789123798213564247138956319675248685942317572364891834591672961827435 # 12 123456789456789123798213564249561837637894251815327496372945618564138972981672345 # 12 123456789456789123798231645267198534581643972934572816349867251672315498815924367 # 15 NA = 2 123456789456789123798231645267843591815697234934125867372918456581364972649572318 # 15 123456789456789132789231564218647395394518627675923841531894276847162953962375418 # 25 NA = 2 123456789456789132789231564234678915861925473975143628317894256592367841648512397 # 25 123456789456789132789231564235697418671842395948315627394178256567923841812564973 # 25 123456789457189623689732145236578914795214836841963257378625491564891372912347568 # 250

by **Serg** » Tue Jul 05, 2022 3:14 pm

Hi, Mathimagics!
Very interesting findings!

Mathimagics wrote:There are only 9 grids with this property. In this list they are tagged with band# and automorphism count (7 of the 9 are automorphic):

Do you mean an automorphic grid must have at least one non-trivial automorphism (besides "identity" transformation)?

Mathimagics wrote:
Code: Select all
123456789456789123798231564275943618369815472841627395587362941612594837934178256 # 14 123456789456789123897231645231564978645978231978312564369147852582693417714825396 # 17 NA = 6 123456789456789123897231645231564978645978231978312564369825417582147396714693852 # 17 NA = 6 123456789456789231789123645231564897564897312897231456375618924618942573942375168 # 27 NA =36 123456789456789231789123645231564897564897312897231456375942168618375924942618573 # 27 NA =18 123456789456789231789123645231564897564897312978312564395248176617935428842671953 # 27 NA = 6 123456789456789231789123645231564897564897312978312564395671428617248953842935176 # 27 NA = 6 123456789456789231789123645231564978564897123897231564375942816618375492942618357 # 27 NA =36 123456789457289163698713254261847935579362841834591627315928476786134592942675318 # 354

What do they mean numbers after "#" (14, 17, etc.)?

Are known lowest clue numbers of valid puzzles for those 9+8 grids? Are known TNC numbers for grids with 17-clue puzzles and average TNC number for all ED grids?

Serg

by **coloin** » Tue Jul 05, 2022 4:05 pm

Red Ed [ahead of his time] did visit this subject 127 fully entwined grids
All your cycle length 9 are in this list ...
All the 127 grids have all 36 pairs of clues as a 18C UA

by **coloin** » Tue Jul 05, 2022 4:18 pm

He also [rather easily] found this grid with 78 pairs ["probably"] is the maximum.

Code: Select all: +---+---+---+ |123|456|789| |457|189|326| |689|327|154| +---+---+---+ |231|645|897| |745|891|632| |896|732|541| +---+---+---+ |318|264|975| |574|918|263| |962|573|418| +---+---+---+ Platinum Trellis

by **m_b_metcalf** » Tue Jul 05, 2022 4:52 pm

coloin wrote:Red Ed [ahead of his time] did visit this subject 127 fully entwined grids
All your cycle length 9 are in this list ...
All the 127 grids have all 36 pairs of clues as a 18C UA

I fired up my program before reading that thread, and stopped it when it found its first 20C:

Code: Select all: 1 . 3 . . . . . . . 5 6 7 . . . . . . . . 2 . . . . 4 . . . 9 . . 6 . 8 3 . 9 . 1 . . . . . . . . . . . . 5 5 8 7 . . . . . . . . . . 9 . . 3 . . . . . . 8 . . . 20C, very easy 1.3.......567........2....4...9..6.83.9.1............5587..........9..3......8... 2.

Mike

by **Mathimagics** » Tue Jul 05, 2022 5:54 pm

Hi Serg!

the numbers following the # are the grid's band number, and where the grid has non-trivial automorphisms, NA is the size of the automorphism group

loosely speaking (always problematic, I know), we usually say a grid is automorphic to mean it has non-trivial automorphisms, ie NA > 1

Serg wrote:Are known lowest clue numbers of valid puzzles for those 9+8 grids? Are known TNC numbers for grids with 17-clue puzzles and average TNC number for all ED grids?

I do have the answers to all of these questions. I was actually in the process of writing a follow-up post with additional results, so watch this space ... 8-)

coloin wrote:Red Ed [ahead of his time] did visit this subject (cf 127 fully entwined grids)
All your cycle length 9 are in this list ...
All the 127 grids have all 36 pairs of clues as a 18C UA

Hi coloin,
All of the grids in my list, with TNC = 36 , have 36 x minimal 2-digit UA18's. But the "fully entwined" grid list includes more with TNC > 36, so I am unsure of the definition of "fully entwined" ... could it be this?

for any pair {AB}, the cycles are all UA's (4, 6, .. 18), and their union results in a UA18

(for an individual 2-digit cycle to be a UA, it must satisfy the "box rule", which means the cycle must include 2 cells from each box visited in the cycle)

[EDIT] this can't be right, because the PT grid, below, for the pair {45}, has a valid UA6 + a valid UA12

Red Ed wrote:A systematic search for grids with no fully-entwined pairs yields just one answer, up to isomorphism, namely this 78 (which I suppose we could call the "Platinum trellis", Pt, atomic number 78):
Code: Select all
123|456|789 457|189|326 689|327|154 ---+---+--- 231|645|897 745|891|632 896|732|541 ---+---+--- 318|264|975 574|918|263 962|573|418

Ok, so this has NO fully-entwined pairs, but has 78 somethings ... but what?

by **coloin** » Tue Jul 05, 2022 6:24 pm

Mathimagics wrote:But the "fully entwined" grid list includes more with TCN > 36, so I am unsure of the definition of "fully entwined"

Hmmm i assumed that the TCN of these grids was 36 ...... ?

Only one of Red Ed's grids was found to have [3] 17s the - SFB grid.
The rest presumably all have 18s ... which is also a presumption !! :roll:

Hidden Text: Show

The PT grid has 78 2clue unavoidabes
output from nppcsu - it looks like the cells are numbered 11-99 r1c1 - r9c9

Code: Select all: 123456789 457189326 689327154 231645897 745891632 896732541 318264975 574918263 962573418 {11,12,24,28,35,37,41,43,72,74,85,87,93,98,} {56,59,66,69,} {11,13,42,43,71,72,} {24,27,34,37,} {56,58,65,69,85,89,96,98,} {11,14,21,24,} {37,39,68,69,97,98,} {43,45,52,56,72,76,83,85,} {11,15,22,24,37,38,67,69,72,79,81,85,94,98,} {43,46,53,56,} {11,16,24,29,31,37,43,44,56,57,63,69,} {72,75,85,88,92,98,} {11,17,23,24,36,37,43,49,51,56,64,69,} {72,78,82,85,95,98,} {11,18,32,37,43,47,61,69,72,73,98,99,} {24,25,54,56,85,86,} {11,19,33,37,43,48,62,69,72,77,91,98,} {24,26,55,56,84,85,} {12,13,34,35,41,42,65,66,71,74,93,96,} {27,28,58,59,87,89,} {12,14,21,28,35,39,41,45,52,59,66,68,74,76,} {83,87,93,97,} {12,15,22,28,35,38,} {41,46,53,59,66,67,74,79,81,87,93,94,} {12,16,31,35,41,44,63,66,74,75,92,93,} {28,29,57,59,87,88,} {12,17,23,28,35,36,64,66,74,78,82,87,93,95,} {41,49,51,59,} {12,18,25,28,32,35,} {41,47,54,59,61,66,73,74,86,87,93,99,} {12,19,26,28,33,35,41,48,55,59,62,66,91,93,} {74,77,84,87,} {13,14,21,27,34,39,71,76,83,89,96,97,} {42,45,52,58,65,68,} {13,15,22,27,34,38,42,46,53,58,65,67,94,96,} {71,79,81,89,} {13,16,31,34,42,44,63,65,71,75,92,96,} {27,29,57,58,88,89,} {13,17,23,27,} {34,36,64,65,95,96,} {42,49,51,58,71,78,82,89,} {13,18,25,27,32,34,42,47,54,58,61,65,71,73,} {86,89,96,99,} {13,19,26,27,33,34,71,77,84,89,91,96,} {42,48,55,58,62,65,} {14,15,38,39,45,46,67,68,76,79,94,97,} {21,22,52,53,81,83,} {14,16,44,45,75,76,} {21,29,31,39,} {52,57,63,68,83,88,92,97,} {14,17,36,39,45,49,64,68,76,78,95,97,} {21,23,51,52,82,83,} {14,18,21,25,32,39,45,47,52,54,61,68,97,99,} {73,76,83,86,} {14,19,21,26,33,39,76,77,83,84,91,97,} {45,48,52,55,62,68,} {15,16,22,29,31,38,44,46,75,79,81,88,92,94,} {53,57,63,67,} {15,17,36,38,46,49,64,67,78,79,94,95,} {22,23,51,53,81,82,} {15,18,22,25,32,38,} {46,47,53,54,61,67,73,79,81,86,94,99,} {15,19,22,26,33,38,46,48,53,55,62,67,77,79,} {81,84,91,94,} {16,17,23,29,31,36,44,49,51,57,63,64,} {75,78,82,88,92,95,} {16,18,25,29,31,32,61,63,73,75,86,88,92,99,} {44,47,54,57,} {16,19,26,29,} {31,33,62,63,91,92,} {44,48,55,57,75,77,84,88,} {17,18,23,25,32,36,47,49,73,78,82,86,95,99,} {51,54,61,64,} {17,19,48,49,77,78,} {23,26,33,36,} {51,55,62,64,82,84,91,95,} {18,19,32,33,47,48,61,62,73,77,91,99,} {25,26,54,55,84,86,} -------------------------------------------------------------------

by **Mathimagics** » Tue Jul 05, 2022 7:19 pm

There are only 9 ED grids with TNC = 36, definitely!

"Fully entwined" is defined in the very first post in that thread. For 2 digits {A,B} it SEEMS to boil down to this:

RW wrote:The digits can be paired in 36 different ways, and the pairs can form 1-4 different deadly patterns each.

If digits {A,B} form 4 deadly patterns, then removing all digits A and B would cause 16 solutions (2^4).

If {A,B} forms only one deadly pattern, then removing all digits A and B would cause 2 solutions. I will call such a pair "fully entwined".

If a pair {A,B} is fully entwined then you can remove all A's and all but one of the B's and still maintain a unique solution.

This all makes sense, "deadly Pattern" seems to mean UA. But the definition seems to imply that "fully entwined" {A,B} is just the same as "has cycle length 9" ...

If {AB} has 2 or more cycles, and all are valid (wrt to the box rule), then you need 1 given for each cycle to get a US (unique solution). See the first grid illustration above - 3 cycles = 3UA's = 3 givens needed.

(BTW, thanks for the list of UA's! I can compare these with my cycle list for the same grid ..

)

by **Mathimagics** » Tue Jul 05, 2022 10:36 pm

Ok, we need to clarify the relationship between cycles and (2-digit) UA's:

every valid cycle (ie. with the "box-valid" property) corresponds to a UA

for any pair {A,B}, any cycles which are not valid can be joined together to form a UA

if all cycles for a pair {A,B} are invalid, then their union forms a UA18

Two examples. On the left (from the "Pt grid" mentioned above, thanks coloin), has 4 cycles for the pair {1,3}, two of which are invalid, but these can be joined to form a UA8.

On the right is a grid from Red Ed's set of 127 grids, showing 4 cycles for the pair {1,6}. None of these are valid UA's, and so their union is a UA18.

And so all the grids in Red Ed's list indeed have 36 x UA18's, but only 9 of them have 36 cycles of length 9.

Mystery solved! Phew ... :roll:

by **coloin** » Tue Jul 05, 2022 10:38 pm

Mathimagics wrote:There are only 9 ED grids with TNC = 36, definitely!

well Red Ed was pretty proud of his Russell's Viper Grid ! which is not in your 9

Code: Select all: 123456789456789123789231564234178956695342817817695342368527491572914638941863275 (RV)

one thing I have learned was that he was almost never wrong and of course Mathimagics is rarely wrong too.....
and am sure there will be a rational elucidating explanation

by **coloin** » Tue Jul 05, 2022 10:42 pm

Indeed

by **coloin** » Tue Jul 05, 2022 11:26 pm

The structure of the solution grid has always been fascinating !
Here are the 181 different ways to have 2 clues in a grid [170 templates]

Hidden Text: Show

Code: Select all: .......12....12....12.............21....21....21.........1..2..1..2.....2.....1.. 16 sol. .......12....12....12.............21....21...12..........1..2.....2..1..2.1...... 16 sol. .......12....12....12.............21....21...12..........1..2....12.....2.....1.. 8 sol. .......12....12....12.............21...12....12............12.....2..1..2.1...... 8 sol. .......12....12....12.............21...12....12............12....12.....2.....1.. 4 sol. .......12....12....12.............21...12....2.1...........12.....2..1..12....... 8 sol. .......12....12....12.............21...12....2.1...........12...2....1..1..2..... 4 sol. .......12....12....12.............21..1.2.....2...1......1..2..1..2.....2.....1.. 8 sol. .......12....12....12.............21..1.2.....2.1..........12..1..2.....2.....1.. 4 sol. .......12....12....12.............21..1.2.....2.1........2..1..1.....2..2....1... 4 sol. .......12....12....12.............21..1.2.....2.1........2.1...1.....2..2.....1.. 8 sol. .......12....12....12.............21..1.2....2..1..........12.....2..1..12....... 4 sol. .......12....12....12.............21..1.2....2..1..........12...2....1..1..2..... 4 sol. .......12....12....12.............21..1.2....2..1........2..1...2...1...1.....2.. 4 sol. .......12....12....12.............21..12......2.1..........12..1...2....2.....1.. 8 sol. .......12....12....12.............21..12......2.1.........21...1.....2..2.....1.. 16 sol. .......12....12....12.............21..12.....2....1.......2.1.....1..2..12....... 4 sol. .......12....12....12.............21..12.....2....1.......2.1...2.1.....1.....2.. 4 sol. .......12....12....12.............21..12.....2..1..........12......2.1..12....... 8 sol. .......12....12....12.............21..12.....2..1..........12...2....1..1...2.... 4 sol. .......12....12....12.............21..12.....2..1.........2.1...2...1...1.....2.. 4 sol. .......12....12....12.............21..12.....2..1.........21....2....1..1.....2.. 8 sol. .......12....12....12.............211..2.....2..1..........12....1.2.....2....1.. 8 sol. .......12....12....12............12....12....12.............2.1...2.1...2.1...... 8 sol. .......12....12....12............12....12....12.............2.1..12.....2....1... 4 sol. .......12....12....12............12....12....12............12....12.....2.......1 2 sol. .......12....12....12............12....12....2.1............2.1...2.1...12....... 8 sol. .......12....12....12............12....12....2.1............2.1.2...1...1..2..... 4 sol. .......12....12....12............12....12....2.1...........12.....2....112....... 4 sol. .......12....12....12............12....12....2.1...........12...2......11..2..... 2 sol. .......12....12....12............12...1.2.....2...1.........2.11..2.....2..1..... 8 sol. .......12....12....12............12...1.2.....2...1......1..2..1..2.....2.......1 4 sol. .......12....12....12............12...1.2.....2.1...........2.11..2.....2....1... 4 sol. .......12....12....12............12...1.2.....2.1..........12..1..2.....2.......1 2 sol. .......12....12....12............12...1.2.....2.1........2....11.....2..2....1... 2 sol. .......12....12....12............12...1.2.....2.1........2.1...1.....2..2.......1 4 sol. .......12....12....12............12...1.2....2....1.........2.1.2.1.....1..2..... 4 sol. .......12....12....12............12...1.2....2....1......1..2.....2....112....... 4 sol. .......12....12....12............12...1.2....2....1......1..2...2......11..2..... 2 sol. .......12....12....12............12...1.2....2....1......2....1.2.1.....1.....2.. 2 sol. .......12....12....12............12...1.2....2..1...........2.1.2...1...1..2..... 4 sol. .......12....12....12............12...1.2....2..1..........12.....2....112....... 2 sol. .......12....12....12............12...1.2....2..1..........12...2......11..2..... 2 sol. .......12....12....12............12...1.2....2..1........2....1.2...1...1.....2.. 2 sol. .......12....12....12............12...1.2....2..1........2.1....2......11.....2.. 2 sol. .......12....12....12............12...12......2.1...........2.11...2....2....1... 8 sol. .......12....12....12............12...12......2.1..........12..1...2....2.......1 4 sol. .......12....12....12............12...12......2.1.........2...11.....2..2....1... 4 sol. .......12....12....12............12...12.....2....1.........2.1.2.1.....1...2.... 4 sol. .......12....12....12............12...12.....2....1.......2...1.2.1.....1.....2.. 2 sol. .......12....12....12............12...12.....2..1..........12...2......11...2.... 2 sol. .......12....12....12............12...12.....2..1.........2...1.2...1...1.....2.. 2 sol. .......12....12....12............12..2.1.....1...2..........2.1..12.....2....1... 4 sol. .......12....12....12............12..2.1.....1...2.........12.....2....12.1...... 2 sol. .......12....12....12............12..2.1.....1...2.........12....12.....2.......1 2 sol. .......12....12....12............12..2.1.....1..2..........12....1.2....2.......1 2 sol. .......12....12....12............12..2.1.....1..2.........2...1..1...2..2....1... 2 sol. .......12....12....12............12.1..2.....2..1..........12....1.2.....2......1 4 sol. .......12....12....12...........1.2...1.2.....2......1...1..2..1..2.....2.....1.. 4 sol. .......12....12....12...........1.2...1.2.....2......1...2..1..1.....2..2..1..... 4 sol. .......12....12....12...........1.2...1.2.....2....1.....1..2..1..2.....2.......1 2 sol. .......12....12....12...........1.2...1.2.....2....1.....2....11.....2..2..1..... 2 sol. .......12....12....12...........1.2...1.2....2.....1.....1..2...2......11..2..... 2 sol. .......12....12....12...........1.2...1.2....2.....1.....2....1.2.1.....1.....2.. 2 sol. .......12....12....12...........1.2...12......2....1......2...11.....2..2..1..... 2 sol. .......12....12....12...........1.2...12......2....1.....1..2..1...2....2.......1 2 sol. .......12....12....12...........1.2...12.....2.......1....2.1...2.1.....1.....2.. 2 sol. .......12....12....12...........1.2...12.....2.......1...1..2...2....1..1...2.... 2 sol. .......12....12....12...........1.2...12.....2.....1......2...1.2.1.....1.....2.. 2 sol. .......12....12....12...........1.2...12.....2.....1.....1..2...2......11...2.... 2 sol. .......12....12....12...........1.2.1...2....2.......1...1..2....12......2....1.. 4 sol. .......12....12....12...........1.2.1...2....2.......1...2..1....1...2...2.1..... 4 sol. .......12....12....12...........1.2.1...2....2.....1.....1..2....12......2......1 2 sol. .......12....12....12...........1.2.1...2....2.....1.....2....1..1...2...2.1..... 2 sol. .......12....12....12...........12....12......2....1.....1...2.1...2....2.......1 2 sol. .......12....12....12...........12....12.....2.......1....2.1...2.1.....1......2. 2 sol. .......12....12....12...........12....12.....2.......1...1...2..2....1..1...2.... 2 sol. .......12..1..2.....2..1..........21.1..2....2..1.........1.2.....2..1..12....... 8 sol. .......12..1..2.....2..1..........21.1..2....2..1.........1.2...2....1..1..2..... 8 sol. .......12..1..2.....2..1.........12..1..2....2..1...........2.1.2..1....1..2..... 8 sol. .......12..1..2.....2..1.........12..1..2....2..1.........1.2.....2....112....... 4 sol. .......12..1..2.....2..1.........12..1..2....2..1.........1.2...2......11..2..... 4 sol. .......12..1..2.....2..1.......1..2....2....112...........2.1...1....2..2..1..... 4 sol. .......12..1..2.....2..1.......1..2....2....112..........12.....1....2..2.....1.. 8 sol. .......12..1..2.....2..1.......1..2....2..1..12...........2...1.1....2..2..1..... 4 sol. .......12..1..2.....2..1.......1..2....2..1..12..........1..2...1..2....2.......1 4 sol. .......12..1..2.....2..1.......1..2....2..1..12..........12.....1....2..2.......1 4 sol. .......12..1..2.....2..1.......1..2..1.2.....2.......1....2.1.....1..2..12....... 4 sol. .......12..1..2.....2..1.......1..2..1.2.....2.......1....2.1...2.1.....1.....2.. 4 sol. .......12..1..2.....2..1.......1..2..1.2.....2.......1...1..2...2....1..1...2.... 4 sol. .......12..1..2.....2..1.......1..2..1.2.....2.....1......2...1.2.1.....1.....2.. 4 sol. .......12..1..2.....2..1.......1..2..1.2.....2.....1.....1..2...2......11...2.... 4 sol. .......12..1..2.....2.1..........12..1..2....2....1.........2.1.2.1.....1..2..... 4 sol. .......12..1..2.....2.1..........12..1..2....2....1......1..2.....2....112....... 4 sol. .......12..1..2.....2.1..........12..1..2....2....1......1..2...2......11..2..... 2 sol. .......12..1..2.....2.1..........12..1..2....2....1......2....1.2.1.....1.....2.. 2 sol. .......12..1..2.....2.1..........12..1..2....2..1...........2.1.2...1...1..2..... 4 sol. .......12..1..2.....2.1..........12..1..2....2..1..........12.....2....112....... 2 sol. .......12..1..2.....2.1..........12..1..2....2..1..........12...2......11..2..... 2 sol. .......12..1..2.....2.1..........12..1..2....2..1........2....1.2...1...1.....2.. 2 sol. .......12..1..2.....2.1..........12..1..2....2..1........2.1....2......11.....2.. 2 sol. .......12..1..2.....2.1..........12..1.2.....2....1.........2.1.2.1.....1...2.... 4 sol. .......12..1..2.....2.1..........12..1.2.....2....1.......2...1...1..2..12....... 2 sol. .......12..1..2.....2.1..........12..1.2.....2....1.......2...1.2.1.....1.....2.. 2 sol. .......12..1..2.....2.1..........12..1.2.....2....1......1..2...2......11...2.... 2 sol. .......12..1..2.....2.1..........12..1.2.....2....1......12.....2......11.....2.. 2 sol. .......12..1..2.....2.1..........12..1.2.....2..1..........12......2...112....... 4 sol. .......12..1..2.....2.1..........12..1.2.....2..1..........12...2......11...2.... 2 sol. .......12..1..2.....2.1..........12..1.2.....2..1.........2...1.2...1...1.....2.. 2 sol. .......12..1..2.....2.1.........1.2.....2.1..12..........1..2...1.2.....2.......1 2 sol. .......12..1..2.....2.1.........1.2.....2.1..12..........2....1.1....2..2..1..... 2 sol. .......12..1..2.....2.1.........1.2....2....112...........2.1...1....2..2..1..... 2 sol. .......12..1..2.....2.1.........1.2....2....112..........1..2...1..2....2.....1.. 2 sol. .......12..1..2.....2.1.........1.2....2....112..........12.....1....2..2.....1.. 4 sol. .......12..1..2.....2.1.........1.2....2..1..12...........2...1.1....2..2..1..... 2 sol. .......12..1..2.....2.1.........1.2....2..1..12..........1..2...1..2....2.......1 2 sol. .......12..1..2.....2.1.........1.2....2..1..12..........12.....1....2..2.......1 2 sol. .......12..1..2.....2.1.........1.2..1..2....2.....1.....1..2...2......11..2..... 2 sol. .......12..1..2.....2.1.........1.2..1..2....2.....1.....2....1.2.1.....1.....2.. 2 sol. .......12..1..2.....2.1.........1.2..1.2.....2.......1....2.1.....1..2..12....... 2 sol. .......12..1..2.....2.1.........1.2..1.2.....2.......1...1..2...2....1..1...2.... 2 sol. .......12..1..2.....2.1.........1.2..1.2.....2.....1......2...1.2.1.....1.....2.. 2 sol. .......12..1..2.....2.1.........1.2..1.2.....2.....1.....1..2...2......11...2.... 2 sol. .......12..1..2.....2.1.........1.2..1.2.....2.....1.....12.....2......11.....2.. 2 sol. .......12..1..2.....2.1.........12......2.1..12..........1...2..1.2.....2.......1 4 sol. .......12..1..2.....2.1.........12.....2....112...........2.1...1.....2.2..1..... 2 sol. .......12..1..2.....2.1.........12.....2....112..........12.....1.....2.2.....1.. 2 sol. .......12..1..2.....2.1.........12...1..2....2.......1...1...2..2....1..1..2..... 2 sol. .......12..1..2.....2.1.........12...1..2....2.......1...2..1...2.1.....1......2. 2 sol. .......12..1..2.....2.1.........12...1.2.....2.......1....2.1...2.1.....1......2. 2 sol. .......12..1..2.....2.1.........12...1.2.....2.......1...1...2..2....1..1...2.... 2 sol. .......12..1..2.....2.1.........12...1.2.....2.......1...12.....2....1..1......2. 2 sol. .......12..1..2.....2.1........21....1.....2.2.....1.....1..2...2......11..2..... 4 sol. .......12..1..2.....2.1........21....1.....2.2.....1.....2....1.2.1.....1.....2.. 4 sol. .......12..1..2.....2.1........21....1....2..2.....1.....1...2....2....112....... 8 sol. .......12..1..2.....2.1.......1...2..1..2....2.....1.....2....1.2...1...1.....2.. 2 sol. .......12..1..2.....2.1.......1...2..1..2....2.....1.....2.1....2......11.....2.. 2 sol. .......12..1..2.....2.1.......1..2...1..2....2.......1...2..1...2...1...1......2. 2 sol. .......12..1..2.....2.1.......1..2...1..2....2.......1...2.1....2....1..1......2. 2 sol. .......12..1..2.....2.1.......12.....1.....2.2.....1.....2.1....2......11.....2.. 4 sol. .......12..1..2.....2.1.......12.....1....2..2.......1...2.1....2....1..1......2. 4 sol. .......12..1..2....2..1..........12...2..1....1..2.......1..2..1..2.....2.......1 4 sol. .......12..1..2....2..1..........12...2..1....1.2.........2...11.....2..2..1..... 2 sol. .......12..1..2....2..1..........12...2..1...1...2.......1..2...1.2.....2.......1 2 sol. .......12..1..2....2..1..........12...2..1...1..2...........2.1.1..2....2..1..... 4 sol. .......12..1..2....2..1..........12...2..1...1..2.........2...1...1..2..21....... 2 sol. .......12..1..2....2..1..........12...2..1...1..2.........2...1.1....2..2..1..... 2 sol. .......12..1..2....2..1..........12...2..1...1..2........12.....1....2..2.......1 2 sol. .......12..1..2....2..1..........12...21.....1...2..........2.1.1.2.....2....1... 4 sol. .......12..1..2....2..1..........12...21.....1...2.........12.....2....121....... 2 sol. .......12..1..2....2..1..........12...21.....1...2.........12...1.2.....2.......1 2 sol. .......12..1..2....2..1..........12..1.2.....2....1.........2.1..21.....1...2.... 4 sol. .......12..1..2....2..1..........12..1.2.....2....1.......2...1...1..2..1.2...... 2 sol. .......12..1..2....2..1..........12..1.2.....2....1.......2...1..21.....1.....2.. 2 sol. .......12..1..2....2..1.........1.2.....2.1..1.2.........1..2...1.2.....2.......1 2 sol. .......12..1..2....2..1.........1.2.....2.1..1.2.........2....1.1....2..2..1..... 2 sol. .......12..1..2....2..1.........1.2.....2.1..21..........1..2....2.....11..2..... 2 sol. .......12..1..2....2..1.........1.2....2..1..1.2..........2...1.1....2..2..1..... 2 sol. .......12..1..2....2..1.........1.2....2..1..1.2.........1..2...1..2....2.......1 2 sol. .......12..1..2....2..1.........1.2....2..1..1.2.........12.....1....2..2.......1 2 sol. .......12..1..2....2..1.........1.2....2..1..21...........2...1..21.....1.....2.. 2 sol. .......12..1..2....2..1.........1.2....2..1..21..........1..2....2.....11...2.... 2 sol. .......12..1..2....2..1.........1.2...2...1...1.2.........2...11.....2..2..1..... 2 sol. .......12..1..2....2..1.........1.2...2...1...1.2........1..2..1...2....2.......1 2 sol. .......12..1..2....2..1.........1.2...2...1..1...2.......1..2...1.2.....2.......1 2 sol. .......12..1..2....2..1.........1.2...2...1..1..2.........2...1.1....2..2..1..... 2 sol. .......12..1..2....2..1.........1.2...2...1..1..2........1..2...1..2....2.......1 2 sol. .......12..1..2....2..1.........1.2..1..2....2.....1.....1..2....2.....11..2..... 2 sol. .......12..1..2....2..1.........1.2..1..2....2.....1.....2....1..21.....1.....2.. 2 sol. .......12..1..2....2..1.........1.2..1.2.....2.....1......2...1..21.....1.....2.. 2 sol. .......12..1..2....2..1.........1.2..1.2.....2.....1.....1..2....2.....11...2.... 2 sol. .......12..1..2....2..1.........12.....2....121...........2.1....21.....1......2. 2 sol. .......12..1..2....2..1.........12.....2....121..........1...2...2...1..1...2.... 2 sol. .......12..1..2....2..1.........12.....2....121..........12......2...1..1......2. 2 sol. .......12..1..2....2..1.........12...1..2....2.......1...1...2...2...1..1..2..... 2 sol. .......12..1..2....2..1.........12...1.2.....2.......1....2.1....21.....1......2. 2 sol. .......12..1..2....2..1.........12...1.2.....2.......1...1...2...2...1..1...2.... 2 sol. .......12..1..2....2..1.......1...2..1..2....2.....1.....2....1..2..1...1.....2.. 2 sol. .....1..2..2....1..1..2.........2..1..1...2..2..1.........1..2..2....1..1..2..... 2 sol. .....1..2..2....1..1..2.........21...2.1.....1......2.....1.2....12.....2.......1 2 sol. .....1..2..2....1..1..2........1.2....12.....2.......1...1...2..2....1..1....2... 2 sol.

Code: Select all: 2 sol. 105 4 sol. 55 8 sol. 18 16 sol. 3 --- 181

Those that have 2 sol are 18C UAs
The "FE" grids all have 18 clue UAs which have 2 sol.
I guess some of these have a cycle length 9
I hope this helps

by **Mathimagics** » Wed Jul 06, 2022 8:27 am

coloin wrote:Red Ed was pretty proud of his Russell's Viper Grid ! which is not in your 9

If you look at the image above, where I give an example of a UA18 implied by a union of invalid cycles, you will see that the grid illustrated is in fact the "RV" grid.

Of the 36 digit pairs, 31 have cycles of length 9, and the other 5 are all like the example ({1,6}) I showed above, they all have 3 invalid cycles, and each forms a UA18.

So the number of UA18's is 36, but the cycle count is TNC = 31 + 5x3 = 46.

:arrow:

BTW, I have rescanned the ED grids to count the 36 x UA18 cases, and I do get 127 grids, so hats off to Ed Russell

coloin wrote:one thing I have learned was that he was almost never wrong and of course Mathimagics is rarely wrong too.....

You must be thinking of somebody else, as my track record is fairly rich in gaffes and public humiliations ...

PS: I did NOT have binary relations with that grid!

by **dobrichev** » Wed Jul 06, 2022 9:01 am

Hi Mathimagics,

You gave an example that demonstrates that Pt grid has at least one non-minimal 2-digit UA18, while the actual claim is that this grid is the only one having NONE such minimal UA18s.
So far I think that Monocyclyc and fully-entwinned grids are the same thing.

by **coloin** » Wed Jul 06, 2022 9:16 am

I think it all helps in understanding and we are indeed wiser
I understand the "cycle" bit now.

For completeness it should be possible to identify this for each of the 105 ED 2 perm UA18s.

The "Monocyclic"grids they must be composed wholly of the monocyclic/namocyclic/cycle9 [ there are indeed 9 !] 2 sol/perm UA18s, [maybe 6 of one type in the automorphics]

The other 76 18C pairs have a cycle determined by their inherent UAs, 2 UA has 4 perms, 3 UA have 8 and 4 UA have 16 perms as was clear before.

And as an additional question
What is the 18C count for each of the FE grids I wonder ? ... Maybe the Monocyclic ones are advantaged - or not :roll:

The New Sudoku Players' Forum

MonoCyclic Grids

MonoCyclic Grids

Re: MonoCyclic Grids

Re: MonoCyclic Grids

Re: MonoCyclic Grids

Re: MonoCyclic Grids

Re: MonoCyclic Grids

Re: MonoCyclic Grids

Re: MonoCyclic Grids

Re: MonoCyclic Grids

Re: MonoCyclic Grids

Re: MonoCyclic Grids

Re: MonoCyclic Grids

Re: MonoCyclic Grids

Re: MonoCyclic Grids

Re: MonoCyclic Grids