The New Sudoku Players' Forum

[Allan Barker]

Dear Denis,

It seems that our understanding is about the same, but there are one or two interesting points.

Allan, I've now read a large part of your website and I have got a more precise idea of your approach. I would not insist on the words "set cover" about it, because this is not the central aspect. The approach is not about transforming the whole Sudoku problem into an exact cover problem.

Yes, correct, the only relation to set-cover is the use of generic cover sets in a way similar to the dual cover process mentioned above, which must have its origins in early "fish" work.

It is about how to combine several set constraints and how to deal with the different "ranks" of these constraints. Most of the currently used rules are rank 0 or 1, for the mere reason that the higher the rank the more complex it becomes to find the patterns.

Right, mixed logic with different ranks is an advanced level and logic with uniform rank is the basic level. The theme is about the uniform properties (rank) over a region of sets, and how regions with different properties relate. Your right that most Sudoku methods are rank 0 or rank 1, but rank 2 logic is sometimes used along the way, such as AALSs.

Allan Barker wrote:

LAS produces static logic meaning there are no sequential steps or starting points, even for chains.

This is not specific to your approach. It seems that some people don't understand that a chain is a static pattern - they want to prove the chain rule every time they use it. They consider a chain as a chain of inferences instead of a static pattern. I've often written about this conceptual error.

Correct, I only point out that inference chains are not required. To me, patterns and inference chains are two ways of looking at the same thing, but of course quite different.

It doesn't seem you have a means of expressing and using sequentiality of patterns.

Not yet, since there was no need, but clearly something is needed for discussion purposes.

Conversely, being static doesn't mean that a chain has to be an unstructured pattern. A chain can be both static and sequentially ordered.

This is correct in this context, however, I was thinking of static vs. sequential more in a temporal sense. (more below)

Allan Barker wrote:

In this sense, the logic is pattern like or pictographic.

Now, the word "pictographic" seems very inappropariate - because of all the permutations that can be applied to a pattern, thus changing drastically its visual appearance without changing its fundamental logical nature. That's a point about your graphics. They are fabulous, but at some point they may hide the underlying logical structure. There's no difference between links along a row, a column or a number: that's what 3D symmetry really means. That's why I write an nrc-link simply as "-", whichever type it is (and others use other notations to the same effect).

Pictograms were meant to suggest features, I had learned to read Chinese at one point. What I really want to compare is how we recognize features and images in parallel whereas we process sequential logical thinking differently. Humans are very good at patterns and can easily see a chain no matter what the permutations are. Your point about simplified notation and nrc-links is also valid.


Allan Barker wrote:

The biggest distinction is between logic with uniform rank and logic that has regions of mixed rank. Rank is basically related to the number of missing constraints. Expanding on this a little gives the following kinds of logic.
1. Rank 0. Fish like logic, from X-wing to Steve's EM solution.
2. Rank 1. Chain like, Kraken fish, ALS wings and chains.
3. Rank 2, Kraken Blossoms? AALS units.
4. Mixed rank, overlap linksets (weak sets), nrct chains, finned fish.
5. Mixed rank, overlap sets (strong sets), broken wings, proving loops.

I agree that ranks 0, 1, 2 have a profound meaning - in part because they are tightly related to complexity. But "mixed rank" doens't seem to have a very precise meaning. When an nrc(z)(t) chain is built from left to right, it is not mixed rank, it is rank 1. This may be the indication that the notion of sequentiality of a pattern is missing in your approach.

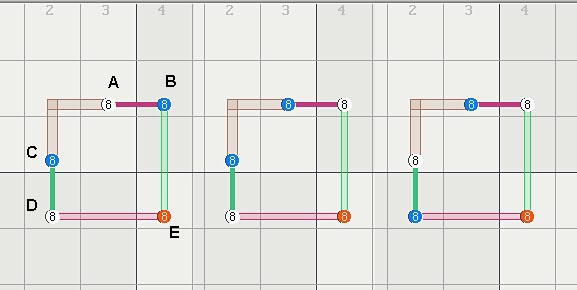
This goes to the heart of the matter. First, I should have given nrc(t)(z) chains more attention but I only listed nrc-t chains, nrc chains would be rank 1. However, a completed nrc-t chain, like the first of the 2 diagrams above, is mixed rank logic at least according to my system.

Now, go through the following situations. With no middle candidate in the top row, this is a rank 1, bi-value chain that eliminates the candidates in the lower right. Second, a middle candidate (X) in the top row not connected anywhere else requires one more linkset and the logic is 4 sets + 6 linksets = rank 2. This logic is uniform rank 2 everywhere and cannot eliminate anything.

Now connect X to some other candidate, Y. By necessity, this makes a triple point where 2 linksets overlap. According to the rules, the logic along the "set" branch is one rank higher. This branch points in the direction of set A, which is also rank 1 and thus eliminates the candidate at the intersection with set F. Eliminations can be caused by set B, which is also rank 1.

If X is wrongly connected to Y at an even node (second diagram above), then the triple-point points in the opposite direction and the logic is rank 1 through sets C and D. The end sets are both rank 2 and cannot make eliminations. Thus, this is not an nrc-t chain.

Thus, this simple set of considerations correctly explains why odd-node linked chains are nrct like and why even-node linked chains are not. It also explains why only one end of the nrct chain causes eliminations, which end does, and even which sets can cause eliminations.

It also predicts (shazam!) that for the even-linked chains, that either end can cause eliminations if it overlaps any of the internal linksets between X and the triple point. This is not true for the nrc-t chains.[/i]

Allan Barker wrote:

Then there are categories that seem to make less difference to the set logic:
1. No. of dimensions, 0D, 1D, 2D, 3D.
2. No. of candidates per set.
3. Branching. (related to no. of candidates per set)

But they make a great difference in terms of complexity of finding the patterns.

OK, good point, I think I would withdraw any real distinction between the first and second list, other than a personal preference on how to catagorize things.

I am not so knowledgeable about complexity, except I seem to make lots of it, or so I am told. However, I think the following two statements are both true. 1. Increasing the number of spatial dimensions allows additional kinds of logic that lead to more complexity. 2. A 3D bi-value (continuous nice) loop has the same complexity as a similar 2D loop.

What would be interesting now is an example of how you solve a puzzle using these rules. It is not yet very clear.

This is also a missing piece on the website. I am preparing something.

[denis_berthier]

Hi Allan,
First, let me recall that I'm discussing all this in detail because I find your approach very interesting. AFAIK, this is the first time a general sound second order rule is proposed in the "condition => action" form, where:
- "condition" bears on subsets of cells and candidates,
- "action" is the assertion of a value or the elimination of (a) candidate(s).
In my terminology, that's what I'd naturally call a second order resolution rule (referring to my definition of a (first order) resolution rule, here: http://forum.enjoysudoku.com/viewtopic.php?t=5600).
(Of course, ALS-chains are an example of a second order resolution rule, but they don't have the same generality as your SecondOrderRuleOfEverything).
As I think this general rule is much too complex to be applied in its full generality by a human player, interesting special cases have to be devised. So you may guess that my main question is: discarding all the already known rules that you have shown your SecondOrderRuleOfEverything subsumes, what would be your next less complex special case of a second order rule? And, of course, we are back to the question of how rules complexities can be defined.

LAS produces static logic meaning there are no sequential steps or starting points, even for chains.

This is not specific to your approach. It seems that some people don't understand that a chain is a static pattern - they want to prove the chain rule every time they use it. They consider a chain as a chain of inferences instead of a static pattern. I've often written about this conceptual error.

Correct, I only point out that inference chains are not required. To me, patterns and inference chains are two ways of looking at the same thing, but of course quite different.

It seems there is some ambiguity about "static". We must distinguish the logical pattern, which is always static (it may have a sequential structure or not - but this structure is always static), and the way the associated rule or eliminations can be proven.
In case the logical pattern has a sequential (static) structure, it is generally the case that the proof of the rule follows this structure (but I wouldn't say the proof is static or not static: the proof is only valid or not valid).
And it is also true that, in your approach, the rules can be proven independently of any sequential structure. As a result, you have e.g. another, non sequential proof, of the nrczt-chain rules.

It doesn't seem you have a means of expressing and using sequentiality of patterns.

Not yet, since there was no need, but clearly something is needed for discussion purposes.

I agree that, in your approach, sequentiality is not needed - in theory. But when it comes to applying the known rules, most of the complex rules are chain rules. And it is likely that finding non anticipative chains using their sequential structure will be easier than finding the corresponding patterns after forgetting this natural ordering.

Conversely, being static doesn't mean that a chain has to be an unstructured pattern. A chain can be both static and sequentially ordered.

This is correct in this context, however, I was thinking of static vs. sequential more in a temporal sense. (more below)

Then I understand "temporal" as "when the player tries to find it".

In this sense, the logic is pattern like or pictographic.

Now, the word "pictographic" seems very inappropariate - because of all the permutations that can be applied to a pattern, thus changing drastically its visual appearance without changing its fundamental logical nature.

Pictograms were meant to suggest features, I had learned to read Chinese at one point. What I really want to compare is how we recognize features and images in parallel whereas we process sequential logical thinking differently. Humans are very good at patterns and can easily see a chain no matter what the permutations are. Your point about simplified notation and nrc-links is also valid.

Although I've very close Chinese friends in Paris, I've always been too lazy to learn Chinese, but AFAIK, Chinese characters can't be submitted to permutations of "rows" and "columns". And they are not so pictographic as it is generally believed. Their original forms, millenia ago, were pictographic, but this is no longer the case. I nevertheless agree that they allow this parallel pattern recognition - as is the case for our writing system: we don't read a letter after the other, but a whole block in a line at once.
The point I wanted to make here is that parallel pattern recognition (which I had also invoked once in another forum), may not be very effective when the same logical pattern can have so many different visual forms. Row, column and number permutations are not among the invariants naturally used by our visual pattern matcher (such as dimension invariants, orientation invariants,...). But I'd be very interested if you have examples to the contrary.
Anyway, yours graphics are great to illustrate how abstract logical patterns can be instantiated in a real grid.

a completed nrc-t chain, like the first of the 2 diagrams above, is mixed rank logic at least according to my system.

I'm not debating this.
My point is that, when seen as an oriented chain which is naturally built from left to right, there is never more than one pending candidate (the current right-linking candidate) - which should allow us to call it rank 1.
As complexity of a pattern is closely related to its rank (though in complex ways), it seems to me that we should always prefer the pattern with smallest rank - or the presentation of the same pattern in the form which makes it to appear with the smallest rank.
As ususal, generality (the subset view) is at variance with efficiency (chain view).

Thus, this simple set of considerations [...] also explains why only one end of the nrct chain causes eliminations, which end does.

I don't understand what you mean. In a pure rnczt-chain, we need an nrc-link from the target to both ends of the chain to have an elimination. Or, in lassos, an nrc-link between candidates of different parities (rl-lassos and lr-lassos).

It also predicts (shazam!) that for the even-linked chains, that either end can cause eliminations if it overlaps any of the internal linksets between X and the triple point. This is not true for the nrc-t chains.

I'm not sure what you mean by an even-linked chain, but it seems to me that it is merely a reversed ordinary nrczt-chain.

I am not so knowledgeable about complexity, except I seem to make lots of it, or so I am told.

I'm not sure anybody can say he is knowledgeable about complexity, at least in its application to Sudoku. See our (short) discussion starting at the bottom of this page: http://forum.enjoysudoku.com/viewtopic.php?t=5600&postdays=0&postorder=asc&start=60
For second order rules, the a priori problem is that if there are X candidates on a grid, there are 2^X subsets of candidates.

However, I think the following two statements are both true. 1. Increasing the number of spatial dimensions allows additional kinds of logic that lead to more complexity. 2. A 3D bi-value (continuous nice) loop has the same complexity as a similar 2D loop.[/i]

Aren't these two statements contradictory? nrc-chains (more or less your "3D bi-value continuous nice loop") are the 3D counterpart of xy-chains (your "2D loop").
Generally speaking, I think we cannot say that the complexity of ruleA is higher than the complexity of ruleB without further qualifications.
Which complexity are we speaking of? Logical complexity (but then how is it defined?)? Complexity of finding the patterns?
As of now, the priorities we've put on our sets of rules are based on intuitive grounds.
We speak a lot of complexity, but what we use in reality is such priorities.

As I now see your approach, and this brings us back to the begining of this post, it may lead to the definition of new second order rules for the extremely hard puzzles. (In addition to examples), the next step could be to define "the next simplest" rank 2 rule.

[Allan Barker]

Denis,

You have posed what is probably the most relevant question, which if I can answer with equal clarity, we will make some progress. Hope to have someting soon. IN the mean time, some kind of notation would be helpful so I will suggest some ideas to see how well they fit.

0. References use RCNB for (row, column, cell, box) in that order.

1. Sets must have 2 coordinates, digit last when possible.
R(row,digit) r12, r89
C(col,digit) c22, c44
N(row,col) n11, n55
B(box,digit) b12, b14

2. Upper case letters RCNB are sets (strong sets) and lower case letters rcnb are linksets (weak sets). R33 vs. r33

3 Nodes have three coordinate with the letter p, i.e., pRCN, or p123

4. A complete rule would be: (logic)implications.
or (sets == linksets)implications.

5. Implications are formed as: linksets => node list
or linksets => node=0, node=1, ...

Rank 0 linkset, clears all external candidates: r19 => p139=0, ...
Rank 1 linkset, clears only overlap: r19+c39 => p139=0

Examples:

X-Wing: (R25 R65 == c25 c65)c25 => p125=0, c65 => p865=0
2 String Kite: (R11 C11 == B11 c51 r51)c51+r51 => p551=0
(notice the 2 string kite has 3 liksets)

It would be nice to make such a notation as simiar to other notation as possible.

[denis_berthier]

Hi Allan,
As you can see from this forum and others, there is no general agreement on notation. If you want to be close to an existing one, you'll have to chose which one. My remarks below are based on mine (the nrc-notation), whose inspiration is set-theoretic.

some kind of notation would be helpful so I will suggest some ideas to see how well they fit.
0. References use RCNB for (row, column, cell, box) in that order.

I'm not sure what you call cell (number from 1 to 81?) but using letter n for it doesn't seem a very good idea.
Personally I never need such a global cell number (I use only row, column, block and square in the block: row-column and block-square are two dual coordinate systems - cell, with this global meaning would be a whole coordinate system in itself).

1. Sets must have 2 coordinates, digit last when possible.
R(row,digit) r12, r89
C(col,digit) c22, c44
N(row,col) n11, n55
B(box,digit) b12, b14

From these examples, I can see you are considering the same rn-, cn-, bn- and rc- spaces as I do (where n is number/digit and not cell). What you call "set" is then a 2D subspace.
In order to avoid any ambiguity, I personally write the values of the coordinates as r1..., c1..., b1..., s1,..., n1...n9
I therefore write r1c2, r8c9, c2n2, c4n4, .... for a cell in one of the 2D spaces.
Depending on how many coordinates are specified, you get either a candidate (3 independent coordinates specified) or a cell in one of the 2D spaces (2 independent coordinates specified).

2. Upper case letters RCNB are sets (strong sets) and lower case letters rcnb are linksets (weak sets). R33 vs. r33

R3n3 = all candidates on row 3 with number coordinate = 3 ?
Sets are sets and can be neither strong nor weak in and by themselves. Mixing the descriptive notion of a set and the way you use it is misleading.

3 Nodes have three coordinate with the letter p, i.e., pRCN, or p123

Why not use simply r1c2n3 ?

4. A complete rule would be: (logic)implications.
or (sets == linksets)implications.

5. Implications are formed as: linksets => node list
or linksets => node=0, node=1, ...

Rank 0 linkset, clears all external candidates: r19 => p139=0, ...
Rank 1 linkset, clears only overlap: r19+c39 => p139=0

I wouldn't use "logic" for the conditions, but "conditions" or "pattern".
I guess you mean a rule is "conditions => conclusions", where conditions is a set of sets and a set of linksets. Using "==" to separate the sets from the linksets may be ambiguous for people used to the Eureka notation.
I wouldn't use "+" instead of "and". This is an unnecessary arbitrary change from logic.
I have to stop now. More of this later.

[Allan Barker]

Denis,

Denis wrote:

I'm not sure what you call cell (number from 1 to 81?) but using letter n for it doesn't seem a very good idea. Personally I never need such a global cell number (I use only row, column, block and square in the block: row-column and block-square are two dual coordinate systems - cell, with this global meaning would be a whole coordinate system in itself)

From these examples, I can see you are considering the same rn-, cn-, bn- and rc- spaces as I do (where n is number/digit and not cell). What you call "set" is then a 2D subspace.

Actually, I think our coordinate systems are probably about the same and in fact, we are using the same N, so maybe it best to explain. For now, forget standard Sudoku cells and digits as I don't rely on either and I will avoid the terms.

The physical picture.

Start with a 9x9x9 cube sitting on a table with a viewer facing one side of the cube. The cube has 729 identical cubical units. Since this is a crystal cube, you can look from any face to the opposite face through 81 channels and each channel has 9 cubical units running from face to face. The 3 cube faces, top, left, and front represent 3 orthogonal groups of 81 channels that intersect. These channels are Sudoku sets and Sudoku rules say that each of the 324 sets (now incluing 81 box sets) must contain exactly one object for a total of 81 objects in the cube. The box sets are horizontal 3x3x1 regions. This is sufficient to define Sudoku and solve puzzles.

Coordinates and labels

The coordinate system is 3D where the left to right channels are rows, front to back channels are columns, top to bottom channels are stacks, and boxes are the horizontal 3x3x1 regions. The 81 objects can be all the same or different, it doesn't matter.

The 3D coordinates are thus row, column, or I could also use x,y,z, where the upper left rear unit is 1,1,1. The four symbols RNCB are used for row, column, stack, and box sets and a fifth symbol P for individual units. RCNB always appear in this order. A set-reference is a single symbol followed by 2 ordered coordinates, i.e., C32 and a point-reference is a P followed by 3 ordered coordinates, p123. Upper and lower case are not special.

Set-references, with symbol, are then Rrn, Ccn, Nrc, and Bbn where b = f(r,c). Locations are Prcn. The center unit of the cube is p555 at the intersection of R55, C55, N55, and B55.

Thus, I have three primary coordinates, r, c, and n. For computational reasons I have used b, a, and n as primary coordinates, where a is an index into a box set's 9 units. I have fast transforms for ban -> rcn as well as transforms for rcn -> nrc -> cnr to optimize candidate alignment in memory.

So, I think what I am using is equvalent to your two systems row-col and block-square which, by my way of thinking, I would write as RCN and BSN.

However, I see I am still struggling with terminology, thus far I did not mention cell or digit, but I often use "cell" instead of stack because the stack is equivalent to traditional 2D cells. I also use digit because, digits correspond to the N coordinate value. I see where this can be confusing.

I still find adjacent coordinates easier on my eyes, i.e., r12+c52 => p152=0, probably because I am used to it, but this does require a higher level ofunderstanding from the reader.

[denis_berthier]

So, I think what I am using is equvalent to your two systems row-col and block-square which, by my way of thinking, I would write as RCN and BSN.

Right. The main difference is that I always use a prefix letter with each coordinate: rows are r1, r2,...; numbers (digits / symbols / your "stacks") are n1, n2, ...
An rc-cell, which is also the set of number-candidates in it, is r1c3,...
An rn-cell, which is also the set of column-candidates in it, is r1n3,... (I would never write r13 which is ambiguous and will be given a different meaning in the Eureka notation.)
A 3D cell, which is also an nrc-candidate, is n1r3c7 or n1b3s7 or n1r3c7b3 (redundancy is not a problem).
The context is always clear enough to disambiguate this quasi assimilation of a 2D (resp. 3D) cell with a set of candidates of the remaining dimension (resp. a candidate).

I still find adjacent coordinates easier on my eyes, i.e., r12+c52 => p152=0, probably because I am used to it, but this does require a higher level of understanding from the reader.

Unless I'm misunderstanding, by r12+c52 you mean an intersection. The algebraic operation associated with intersection is *, + being associated with union (say via the characteristic functions). r12+c52 is thus very misleading.

Finding a good notation is a hard problem. And it can't be dissociated from what you want to express.
When I introduced the xyt, hxyt and then nrct chains, I needed an easy and intuitive way of expressing the content of 2D cells (either rc, rn, cn or bn). I naturally chose the {} symbols from set theory. r1c2{n3 n5} means: the content of cell r1c2 is the set {n3 n5}. You can also have optional candidates (in parens): r1c2{n3 n5 (n4)} and optional (t or z) candidates r1c2{n3 n5 n6# n7*}.
Similarly, r1n2{c3 c5} means: the content of rn-cell r1n2 is the set {c3 c5} ....
There is no easy way in the NL or Eureka notation of expressing nrczt-chains.

It seems to me that you need to express:
- sets, with their precise content, which always specifies the full content of a 2D-cell - for which r1c2{n1 n2 n3} or r1n2{c1 c3 c7} would be most natural;
- linksets, which are also always 2D-cells and whose content has a necessary part and an optional (unspecified) part - for which r1c2{n1 n2 ....} would be most natural.


As for the conclusions: "p152=0" or "p152=1", which I understand as r1c5 <> 2, resp. r1c5 = 2, as everybody writes it this last way, it'b be better not to change this. (p152 may be a good internal representation for your program but not for displaying results).

[Steve K]

Allan, one could formally generalize all uniqueness dedcutions as almost continuous network overlap. In your approach, this would be analagous to "potential rank 0 overlap". I was wondering if you have considered any research into this area, (beyond that cited on your web pages.)

[Allan Barker]

Steve K
Steve,

Sorry, I have been away for a while. No, I have not done anything beyond what is on my website where I show that unique rectangles are rank 0, and, clear every set containing the candidates, which means they no longer have any connection to the puzzle, like a single.

I know set theory will produce two solutions for a true unique rectangle. I have not looked at how it solves the almost continuous network overlap cases, but this is interesting. I will take a look and put the results under the page on unique rectangles.

[champagne]

Hi Allan,

Since it has been proven (waiting for the results, but I am confident that it will come) that your rules are doing something else that what my own set can achieve, I am working on your set of rules.

Here, I just re activate that thread to put it in the "working area".

I think your website is missing a kind of methodology to extract relevant patterns. As I like to work on examples, I start thinking how I can find rank0 patterns with my solver layout (including, why not, accelerators based on tagging).

If I am successfull, I'll try to share my experience in that specific field.

[Allan Barker]

Since it has been proven (waiting for the results, but I am confident that it will come) that your rules are doing something else that what my own set can achieve, I am working on your set of rules.

I may have found what the difference is and I have put the ideas in a new thread about Fata Morgana. It shouldn't be long until I put the full solution on my website but the most relevant part is probably in the new thread.

I think your website is missing a kind of methodology to extract relevant patterns. As I like to work on examples, I start thinking how I can find rank0 patterns with my solver layout (including, why not, accelerators based on tagging).

Your point is both correct and important. My website in fact has no methodology on how to find logic. So far it has been exploratory and working out rules that best explain what the sovlers find. I have tried to provide examples with simple (sink or swim, as you call it ) descriptions. Sheesh, I deserve that one.

However, its probably a good time to think about how to find logic and if you look at the examples you will see almost every kind of pattern. I have some vague ideas and it would be interesting to see yours as well.

[champagne]

Hi Allan,

I re use that post to summarize How I understand the process to extract relevant groups of sets.


1) You build groups of sets to be studied (whatever is the process)

2) you extract the list of candidates. They become colums in the matrix.

3) key point to understand the word "permutation"

You look for all different ways to fill the sets according to sudoku rules.
. each possibility is called a "permutation"
. each permutation has a corresponding row in the matrix
. if a candidate belong to that permutation, the column is set to 1, if not, to 0.

4) At the end

. a column filled with 0 is a candidate that can be cleared
. a column filled with 1 is a candidate assigned.

5) If any of these two case appears, then you start looking for a set/linkset analysis to explain why.

Here your example for such a matrix in an X-Wing structure.

Code: Select all

2 digit plane with node labels - X-Wing

c      c
0      4

A - -  B - -    row 0
- - -  - - -
- - -  - - -

C - -  D - -    row 4
- - -  F - -
E - -  - - -

               ABCD EF
             +--------------
Permutations | 0110 00
             | 1001 00
               ^^--------- row 0
                 ^^------- row 4
               ^-^--^----- col 0
                ^-^--^---- col 4

[Allan Barker]

Champagne, OK, I think I understand. The permutations I use are the different allowed true/false values of the nodes in a piece of logic. This is represented by 1s and 0s. A 3 node set can have 3 valid permutations {1,0,0}, {0,1,0}, and {0,0,1} according to the Sudoku rule. {1,1,0} would be illegal by the Sudoku rule. These permutations are kind of like the permutations in probability theory.

I see the term permutations is also used in Sudoku (more often) to talk about morphing puzzles, where rows, columns, or digits are interchanged. I don't do this type of permutation.

I think it might be more interesting to impliment the actual rank rules and triplet rules, which I have not done but I do have some ideas how it might be done. It would take a couple of days to organzie my thoughts on this. Using these rules might make a powerful and efficient solver, perhaps tagging could also be used?

[champagne]

I see the term permutations is also used in Sudoku (more often) to talk about morphing puzzles, where rows, columns, or digits are interchanged. I don't do this type of permutation.

I think it might be more interesting to impliment the actual rank rules and triplet rules, ...... Using these rules might make a powerful and efficient solver, perhaps tagging could also be used?

1) I don't know about others, but for me, when I red your methodology, the fact that you were working only on sets and the way you defined a permutation pushed me in the "most often used" definition of permutation in the sudoky world. It's OK now.

2) I see an evident use of tagging as "accelerator" when you are working on systems equivalent to AICs including strong links. This does not apply to FM loops. I will develop later.

3) I agree that to have a "solver type" use of your rules you must reach a kind of automatic "humanized solution" of a clearing/assigning group of sets.

ps you have likely seen that I updated my post just above


champagne

[champagne]

Along the same lines. FM loop 2 will eliminate the same two candidates as FM loop1, 2r4c2, 4r4c2, meaning FM loop 1 is not needed, if you have FM loop2.

.

let me start with that statement.

If I understand well your method, I have a much better ides Just take the full group of sets. You'll have only one "permutation" and in once
all candidates to keep
all candidates to clear.



Just to introduce a tentative summary of what I understand from your method and how I see it can be implemented in a solver.

The strong and new Idea in your method is for me to work on subgroups of your “sets” “row, column, node”. The second key issue is the set/link set construction.

The way I now understand it, I would split the process in three parts.

1) defining subgroups,
2) looking for “arrangements of candidates” fitting the group according to SUDOKU rules, the so called "permutation".
3) If possibilities of clearing, assignment appear , looking for the best “set/link sets” arrangements explaining clearings and assignments.

Point 2 is just a technical issue on a well known procedure. It is somehow counting the number of solutions on a partial group of sets.

Point 1 is a hidden key issue. As I said , a trivial solution is to use the full group of sets.
Point 1 must give groups of sets in a sequence as close as possible of growing complexity in point 3. Several strategies can be applied to reach that goal leading likely to different paths in the solution.

Point 3 must be a well defined procedure that the solver can apply. I find a lot of clues reading your documentation, but only clues. The process includes the split in sets and link sets and the rule to find the rank of each set( or link set).

Last remark, when the size of the group of sets increases, point 3 difficulty grows “exponentially”.

Your comments could help going ahead.

champagne

[Allan Barker]

Very Broad View of Permutations

Long ago in the murky past, living creatures developed two powerful abilities, pattern recognition and the ability to recognize multiple outcomes, i.e., to piece things together. In Sudoku, these relate to patterns and permutations.

If a pattern is what makes an elimination, then permutations are the logical why.

In this sense, permutations are a logical representation of the ways candidates can be legally arranged. Below is a simple two-string kite pictured with its three legal permutations, true candidates are shown in white.



If AB and CD are the two strong sets and E is the eliminatee, the allowed permutations can be written as:

Code: Select all

ABCD  E
------------
1001  0
0110  0
0101  0

Looking at all ways to arrange a candidate, if one candidate must always be 0, then that candidate can be eliminated. If a candidate is always 1, then it can be assigned. Such permutation 'reasoning' is probably involved in most Sudoku methods. The concept of a matrix is not needed.

Edit: replaced "string sets" with "strong sets"