The New Sudoku Players' Forum

[mith]

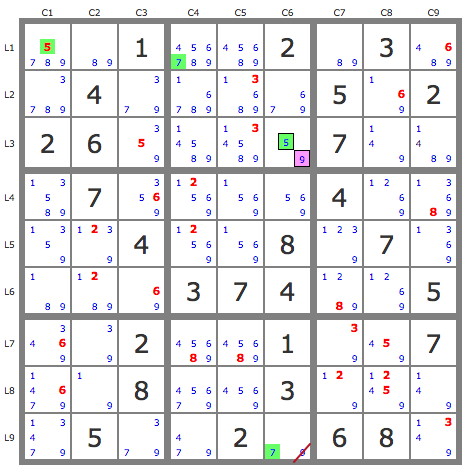
Code: Select all

+-------+-------+-------+
| . . 1 | . . 2 | . 3 . |
| . 4 . | . . . | 5 . 2 |
| . 6 . | . . . | 7 . . |
+-------+-------+-------+
| . 7 . | . . . | 4 . . |
| . . 4 | . . 8 | . . . |
| . . . | 3 7 . | . . 5 |
+-------+-------+-------+
| . . 2 | . . 1 | . . 7 |
| . . 8 | . . 3 | . . . |
| . 5 . | . 2 . | 6 8 . |
+-------+-------+-------+
..1..2.3..4....5.2.6....7...7....4....4..8......37...5..2..1..7..8..3....5..2.68.

[Mauriès Robert]

Hi mith,
I don't see the trap. Here is my resolution after simplifying the puzzle with the basic techniques.

puzzle: Show

P'(9r3c6) : (-9r3c6)=> 5r3c6->5r1c1->7r1c4->7r9c6->... => -9r9c6 => r9c6=7, stte.
We also notice that the puzzle presents several fishs that generate many eliminations.
Robert

[mith]

Yes, the "trap" is more to do with the fish path. (It's not really a trap, just something I found amusing about it.)

This is what the title really comes from...

[SteveG48]

Code: Select all

 *-----------------------------------------------------------------------------*
 | 5-7     89      1       |d4567   d456     2       | 89      3      d46      |
 | 3789    4      a379     | 1689-7  13689   69-7    | 5       169     2       |
 | 2       6       359     | 14589   134589 c59      | 7       149     1489    |
 *-------------------------+-------------------------+-------------------------|
 | 13589   7       3569    | 12569   1569    569     | 4       1269    13689   |
 | 1359    1239    4       | 12569   1569    8       | 1239    7       1369    |
 | 189     1289    69      | 3       7       4       | 1289    1269    5       |
 *-------------------------+-------------------------+-------------------------|
 | 46      39      2       | 4568    4568    1       | 39      45      7       |
 | 14679   19      8       | 45679   4569    3       | 129     12459   149     |
 | 13479   5      b379     | 479     2      c79      | 6       8       1349    |
 *-----------------------------------------------------------------------------*


7r2c3 = r9c3 - (7=95)r39c6 - (5=467)r1c349 => -7 r1c1,r2c46 ; stte

[Cenoman]

7r2c3 = r9c3 - (7=95)r39c6 - (5=467)r1c349 => -7 r1c1,r2c46 ; stte

...shorter: (7=95)r39c6 - (5=467)r1c349 => -7 r2c6; stte

[pjb]

Code: Select all

a57      89      1      | 467-5  46-5    2    | 89     3      46     
 3789    4      b379    | 16789  13689   679  | 5      169    2     
 2       6       39-5   | 14589  134589 e59   | 7      149    1489   
------------------------+---------------------+---------------------
 13589   7       3569   | 12569  1569    569  | 4      1269   13689 
 1359    1239    4      | 12569  1569    8    | 1239   7      1369   
 189     1289    69     | 3      7       4    | 1289   1269   5     
------------------------+---------------------+---------------------
 46      39      2      | 4568   4568    1    | 39     45     7     
 14679   19      8      | 45679  4569    3    | 129    12459  149   
 13479   5      c379    | 479    2      d79   | 6      8      1349   


(5=7)r1c1 - (7)r2c3 = (7)r9c3 - (7=9)r9c6 - (9=5)r3c6 => -5 r1c45, r3c3; stte

Phil

[denis_berthier]

Using only Subsets and a bivalue-chain[3]

Code: Select all

***********************************************************************************************
***  SudoRules 20.1.s based on CSP-Rules 2.1.s, config = BC+SFin
***  Using CLIPS 6.32-r773
***********************************************************************************************
singles ==> r6c6 = 4, r5c8 = 7, r3c1 = 2
212 candidates, 1418 csp-links and 1418 links. Density = 6.34%
whip[1]: c3n6{r6 .} ==> r6c1 ≠ 6, r4c1 ≠ 6, r5c1 ≠ 6
naked-pairs-in-a-row: r7{c2 c7}{n3 n9} ==> r7c8 ≠ 9, r7c5 ≠ 9, r7c4 ≠ 9, r7c1 ≠ 9, r7c1 ≠ 3
naked-pairs-in-a-row: r1{c2 c7}{n8 n9} ==> r1c9 ≠ 9, r1c9 ≠ 8, r1c5 ≠ 9, r1c5 ≠ 8, r1c4 ≠ 9, r1c4 ≠ 8, r1c1 ≠ 9, r1c1 ≠ 8
x-wing-in-columns: n3{c2 c7}{r5 r7} ==> r5c9 ≠ 3, r5c1 ≠ 3
x-wing-in-columns: n5{c3 c6}{r3 r4} ==> r4c5 ≠ 5, r4c4 ≠ 5, r4c1 ≠ 5, r3c5 ≠ 5, r3c4 ≠ 5
x-wing-in-columns: n7{c3 c6}{r2 r9} ==> r9c4 ≠ 7, r9c1 ≠ 7, r2c4 ≠ 7, r2c1 ≠ 7
x-wing-in-rows: n9{r1 r7}{c2 c7} ==> r8c7 ≠ 9, r8c2 ≠ 9, r6c7 ≠ 9, r6c2 ≠ 9, r5c7 ≠ 9, r5c2 ≠ 9
17 singles
whip[1]: r9n9{c6 .} ==> r8c4 ≠ 9, r8c5 ≠ 9
finned-x-wing-in-rows: n6{r5 r1}{c9 c5} ==> r2c5 ≠ 6
swordfish-in-columns: n6{c3 c6 c8}{r6 r4 r2} ==> r4c5 ≠ 6, r4c4 ≠ 6, r2c4 ≠ 6
naked-pairs-in-a-block: b5{r4c4 r4c5}{n1 n9} ==> r5c5 ≠ 9, r4c6 ≠ 9
whip[1]: b5n9{r4c5 .} ==> r4c3 ≠ 9
naked-triplets-in-a-column: c5{r1 r5 r8}{n4 n5 n6} ==> r7c5 ≠ 6, r7c5 ≠ 5, r7c5 ≠ 4, r3c5 ≠ 4
singles ==> r7c5 = 8, r2c4 = 8
x-wing-in-columns: n4{c5 c9}{r1 r8} ==> r8c8 ≠ 4, r8c4 ≠ 4, r8c1 ≠ 4, r1c4 ≠ 4
naked-triplets-in-a-column: c4{r3 r4 r9}{n4 n1 n9} ==> r7c4 ≠ 4
biv-chain[3]: r3c6{n5 n9} - r9c6{n9 n7} - b2n7{r2c6 r1c4} ==> r1c4 ≠ 5
whip[1]: c4n5{r8 .} ==> r8c5 ≠ 5
biv-chain[3]: b9n4{r7c8 r8c9} - r8c5{n4 n6} - b7n6{r8c1 r7c1} ==> r7c1 ≠ 4
stte

[denis_berthier]

P'(9r3c6) : (-9r3c6)=> 5r3c6->5r1c1->7r1c4->7r9c6->... => -9r9c6 => r9c6=7, stte.

What does the "..." stand for?

Using a function I coded recently in CSP-Rules

Code: Select all

(try-to-eliminate-candidates "..1..2.3..4....5.2.6....7...7....4....4..8......37...5..2..1..7..8..3....5..2.68." (create$ 996))

I get the following whip doing the same elimination:

Code: Select all

whip[4]: r3c6{n9 n5} - r1n5{c5 c1} - r1n7{c1 c4} - b8n7{r8c4 .} ==> r9c6 ≠ 9

[Mauriès Robert]

P'(9r3c6) : (-9r3c6)=> 5r3c6->5r1c1->7r1c4->7r9c6->... => -9r9c6 => r9c6=7, stte.

What does the "..." stand for?

'...' means that I can continue building the sequence, but it is not useful. I have often used this notation on this forum (see for example here or here ). It also appears in my TDP document.
I have already explained to you my notations P(A)={B1,B2,B3, ...} where P(A,3)={B1,B2,B3}, or as a sequence P(A): B1->B2-B3->... , or P(A,3): B1->B2->B3. So don't be the one who doesn't understand!
Of course, sometimes I forget the '...', but everyone understands all the same.

Using a function I coded recently in CSP-Rules

Code: Select all

(try-to-eliminate-candidates "..1..2.3..4....5.2.6....7...7....4....4..8......37...5..2..1..7..8..3....5..2.68." (create$ 996))

I get the following whip doing the same elimination:

Code: Select all

whip[4]: r3c6{n9 n5} - r1n5{c5 c1} - r1n7{c1 c4} - b8n7{r8c4 .} ==> r9c6 ≠ 9

This shows that your solver is finally doing sequences that I have been doing by hand for years.
Robert

[denis_berthier]

P'(9r3c6) : (-9r3c6)=> 5r3c6->5r1c1->7r1c4->7r9c6->... => -9r9c6 => r9c6=7, stte.

What does the "..." stand for?

'...' means that I can continue building the sequence, but it is not useful.

Yes, useless, as I said before. So, why write them at all?

Using a function I coded recently in CSP-Rules

Code: Select all

(try-to-eliminate-candidates "..1..2.3..4....5.2.6....7...7....4....4..8......37...5..2..1..7..8..3....5..2.68." (create$ 996))

I get the following whip doing the same elimination:

Code: Select all

whip[4]: r3c6{n9 n5} - r1n5{c5 c1} - r1n7{c1 c4} - b8n7{r8c4 .} ==> r9c6 ≠ 9

This shows that your solver is finally doing sequences that I have been doing by hand for years.

ROFL!
Whips (then named nrczt-chains) have been defined in HLS and coded in SudoRules in 2007, much before you published anything about tracks.
The only thing I've added recently to SudoRules is the possibility of selecting a target or a set of targets, instead of proceeding systematically by simple-first search.

Moreover, this puzzle doesn't require any chain of length 4.

[Mauriès Robert]

The only thing I've added recently to SudoRules is the possibility of selecting a target or a set of targets, instead of proceeding systematically by simple-first search.

I refer you to the following thread (here) where I asked you this question :
"Your SudoRules solver is set to find a resolution with the shortest strings and in this case the number of strings used is free. Is it configurable to find a resolution with a minimum number of strings whose length is free or limited?"
and you told me this:
"No, because such a condition is not expressible in purely logical terms."
So I note that now SudoRules is doing it, as I have been doing for a long time, so it is not illogical. That was the subject of my remark.
Robert

[denis_berthier]

The only thing I've added recently to SudoRules is the possibility of selecting a target or a set of targets, instead of proceeding systematically by simple-first search.

I refer you to the following thread (here) where I asked you this question :
"Your SudoRules solver is set to find a resolution with the shortest strings and in this case the number of strings used is free. Is it configurable to find a resolution with a minimum number of strings whose length is free or limited?"
and you told me this:
"No, because such a condition is not expressible in purely logical terms."
So I note that now SudoRules is doing it, as I have been doing for a long time, so it is not illogical. That was the subject of my remark.

There are no "strings" in SudoRules. There are chains.
And, no, restricting the number of chains used in a resolution path cannot be expressed in purely logical terms: a logical theory cannot set limits on the number of steps used in its proofs, let alone specify that this number should be minimised.
SudoRules has never done it and it is in no way doing it now.

The only new thing in SudoRules is an additional function/command that tries to eliminate (a) chosen candidate(s) (instead to trying to completely solve the puzzle, as it does in its normal mode of working). This function relies on exactly the same rules as for full resolution, but it restricts them to the chosen candidate(s). It doesn't find chains that couldn't have been found previously. Notice that in doing so, this function still applies the simplest-first strategy and it will find the shortest chain(s) eliminating the candidate(s)

Generally speaking, the rules introduced in HLS, further refined in PBCS and coded in CSP-Rules may be used in a lot of different ways.
The standard way in CSP-Rules is simplest-first. But I always said that a human solver will generally not use them in such a systematic way.
The new function I introduced allows the specific possibility of applying them to check how easily some candidate one wants to test can be eliminated. This can be combined with e.g. the knowledge that some other candidate is a backdoor.

[SpAce]

Hi Denis and Robert,

P'(9r3c6) : (-9r3c6)=> 5r3c6->5r1c1->7r1c4->7r9c6->... => -9r9c6 => r9c6=7, stte.

What does the "..." stand for?

'...' means that I can continue building the sequence, but it is not useful.

Yes, useless, as I said before. So, why write them at all?

I agree with Denis that the '...' is quite confusing and useless in terms of practical value. However, it seems consistent with Robert's definitions where a track includes all of the candidates that could be placed with basic techniques using a particular generator. As far as I understand, Robert only writes the set or the sequence that is relevant to the specified conclusions, but the '...' implies that there could be more if the process were continued. I see no problem with that. (But I do agree with Denis that the set point of view is not exactly useful, because readers are mostly interested in the construction sequence.)

If I remember correctly, there was also some discussion earlier about the usefulness of continuing such sequences beyond the first conclusions found. I definitely agree with Robert that sometimes it really is very useful.

It's probably hard to see from the whip/braid point of view because they're simple contradiction patterns that are only capable of eliminating the initial assumption. In such cases the shortest possible chain (net) yielding a contradiction is obviously desired, and there's no point in looking any further.

That's not true about verity patterns, such as conjugate tracks, which look for agreements between two options. In that case it's possible, and often useful, to keep building the tracks beyond the first conclusions, because they can yield many more with a single effort. It's exactly the same thing with the GEM-coloring I use.

Those verity conclusions are all related to a single coloring seed, but don't necessarily imply each other (simply), so they can all be useful and solve the puzzle (or a big part of it) when combined. It would be stupid to stop and reset the coloring every time an elimination is found, unless that elimination is critical alone.

When one has found an effective set of verity conclusions using a single coloring, it's always possible (though not necessarily easy or desirable) to combine them into a single step. That's not possible if they're totally unrelated. It's trivial with Robert's tracks, and also with AICs if only extra endpoints are needed to form subchains. I've written many AICs of much more complex cases too, but it's usually clearer to write them as separate steps.

Also, continuing the process may eventually find a contradiction for one of the two parities (or tracks), which solves that particular coloring once and for all (including the previously found verity eliminations, after basics). Of course that case could be written as a single whip or a braid. However, the verity process yields useful results even when a contradiction is not found for the initial seed, which makes it a much more efficient tool for a manual solver.

[denis_berthier]

there was also some discussion earlier about the usefulness of continuing such sequences beyond the first conclusions found. I definitely agree with Robert that sometimes it really is very useful.
It's probably hard to see from the whip/braid point of view because they're simple contradiction patterns that are only capable of eliminating the initial assumption. In such cases the shortest possible chain (net) yielding a contradiction is obviously desired, and there's no point in looking any further.
That's not true about verity patterns, such as conjugate tracks, which look for agreements between two options. In that case it's possible, and often useful, to keep building the tracks beyond the first conclusions, because they can yield many more with a single effort. It's exactly the same thing with the GEM-coloring I use.

Conjugate tracks should not be compared with whips and braids but with forcing-whips and forcing-braids.
The remarks I made about the simplest-first strategy remain valid for them. There are other possible strategies for using forcing-whips/braids.
What the simplest-first strategy allows to observe is that forcing-whips/braids don't appear when whips/braids of same length are active.

[SpAce]

Conjugate tracks should not be compared with whips and braids but with forcing-whips and forcing-braids.

Yes, as I've said before.

The remarks I made about the simplest-first strategy remain valid for them. There are other possible strategies for using forcing-whips/braids.
What the simplest-first strategy allows to observe is that forcing-whips/braids don't appear when whips/braids of same length are active.

I believe that. Even so, you might give more credit to the forcing-whips/braids approach as a practical manual solving strategy. It can yield either normal whips/braids (when a direct contradiction is found for one of the two branches) or verity eliminations (when the two branches agree).

It's more efficient and more fun than looking for direct contradictions only. Furthermore, when a direct contradiction is found that way, it automatically solves something (possibly the whole puzzle) because the remaining option must be true. For that reason one does not have to know the backdoors beforehand to be able to hit them with a high probability. I'd switch to looking for more random direct contradictions only if such binary options have been exhausted (which implies a pretty hard puzzle).