Isolated Subpuzzles and Local Uniqueness
Glyn wrote:If it takes this long to decide what to call it, how long will it take to figure out how it works?
Does everyone even know what "it" is?
Are coloin's illustrations here correct? Allan, it might be helpful if you would post an illustration.
- ronk
- 2012 Supporter
- Posts: 4764
- Joined: 02 November 2005
- Location: Southeastern USA
This "it" is nothing new, but a multisolution puzzle, which can be solved with not very advanced techniques. Its just hard to ignore these obvious UR's
Edit: oops, you didn't mean the puzzle, this was OT.
The other "its" i saw here were a collection of old links. So i agree, that the "it" needs to be defined.
- eleven
- Posts: 3272
- Joined: 10 February 2008
My puzzle was not relevant to your definition and description of an "isolated subpuzzle" which is a fair term for the situation you describe.
I was under the impression that Glyn moved this topic away from denis's to continue the discussion of uniqueness ?
I agree that an example of an "isolated subpuzzle" might also be useful !
And denis's use of the "braid" term is just darn annoying.
Apologies if this is off topic....
My subpuzzle is an example of the situations where using uniqueness methods - potentially you reach the wrong conclusion - especailly as when presented with a "puzzle" you are unaware of its validity.
I was under the impression that Glyn moved this topic away from denis's to continue the discussion of uniqueness ?
I agree that an example of an "isolated subpuzzle" might also be useful !
And denis's use of the "braid" term is just darn annoying.
Apologies if this is off topic....
My subpuzzle is an example of the situations where using uniqueness methods - potentially you reach the wrong conclusion - especailly as when presented with a "puzzle" you are unaware of its validity.
- Code: Select all
"subpuzzle" - outcome using a uniqueness method
- zero valid grid solutions - no solution
- one grid solution - one solution
- two grid solutions - no solution
- three grid solutions - one solution [my example][false]
- more grid solutions - multiple solutions
- coloin
- Posts: 2664
- Joined: 05 May 2005
- Location: Devon
The term Isolated Sub-Puzzles evolved from the other thread. In response to a question, I posted:
After some discussion, the term isolated sub-puzzles came up but it was later suggested that the term was meaningless. Realizing there was no formal definition for such a concept, I posted a tentitive definition as "Isolated Sub-Puzzles", although I had previously used the term "decoupled". That post then became the beginning of this thread. I will keep secret the name of the person who suggested the term isolated, but his initials are DPB. (edit: I now see he has revealed himself)
Whatever way, I think the logical properties of these regions is a very worthy subject, although I don't have much to offer except to point out their logical structure. Here are a couple of pictures to help visualize the logic. I think this is one case where the 3D images serve their purpose
First image, a standard UR. Left: one of 27 possible continuous nice loops, only 4 are required to clear the region. Note: colored bars are strong sets and white bars are linksets. Right. An isolated UR region with all of its 16 sets. At this point, they are all strong links.
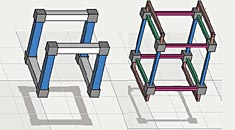
Note the UR must cross one box boundary for there to be 4 box sets, more or less that 1 boundary will not produce the same boxes thus it is not possible to clear all sets contained by the UR. This is set logic reason for the UR rules.
A more complex example embedded in a solved multi-solution puzzle. Box set are left out for clarity. Note, this structure is not 3 rectangles (cubes) that are superimposed, rather it begins to have som logical structure like fish (look vertically). A sowrdfish does not need to have all 9 of its possible candidates occupied. The same is here.
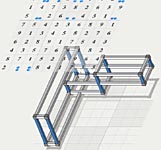
.
Allan Barker wrote:..... I observed that unique rectangles have a unique set/linkset structure that clears candidates from all row, column, box, and cell sets occupied by the solution candidates, for each solution. Kind of like a super nice loop. This makes the UR logically decoupled from the rest of the puzzle, just like a single.
After some discussion, the term isolated sub-puzzles came up but it was later suggested that the term was meaningless. Realizing there was no formal definition for such a concept, I posted a tentitive definition as "Isolated Sub-Puzzles", although I had previously used the term "decoupled". That post then became the beginning of this thread. I will keep secret the name of the person who suggested the term isolated, but his initials are DPB. (edit: I now see he has revealed himself)
Whatever way, I think the logical properties of these regions is a very worthy subject, although I don't have much to offer except to point out their logical structure. Here are a couple of pictures to help visualize the logic. I think this is one case where the 3D images serve their purpose
First image, a standard UR. Left: one of 27 possible continuous nice loops, only 4 are required to clear the region. Note: colored bars are strong sets and white bars are linksets. Right. An isolated UR region with all of its 16 sets. At this point, they are all strong links.

Note the UR must cross one box boundary for there to be 4 box sets, more or less that 1 boundary will not produce the same boxes thus it is not possible to clear all sets contained by the UR. This is set logic reason for the UR rules.
A more complex example embedded in a solved multi-solution puzzle. Box set are left out for clarity. Note, this structure is not 3 rectangles (cubes) that are superimposed, rather it begins to have som logical structure like fish (look vertically). A sowrdfish does not need to have all 9 of its possible candidates occupied. The same is here.

.
Last edited by Allan Barker on Wed Nov 12, 2008 2:46 am, edited 1 time in total.
- Allan Barker
- Posts: 266
- Joined: 20 February 2008
coloin wrote:I was under the impression that Glyn moved this topic away from denis's to continue the discussion of uniqueness ?
I think so, either I or Glyn can change the title to .... Uniqueness and Isolated Sub-Puzzles"???? or what ever is voted as useful. I don't think ISPs alone areenough to support a thread.
coloin wrote:I agree that an example of an "isolated subpuzzle" might also be useful !
I just posted a couple of images. At least this is how they look in terms of sets. I have one more that I am working, an example that is heavily connected to the rest of the puzzle. Will add in a bit. My internet response time is sometimes a bit slow.
.
- Allan Barker
- Posts: 266
- Joined: 20 February 2008
I hate to belabor the point since I think we all understand what isolated subpuzzle means, but please indulge me as I'm terribly confused.
Okay, I'm with you here.
I didn't see this in JPF's definition. I would have called this a valid puzzle (or a sudoku).
Here is where my confusion starts. JPF defines a subpuzzle as
It says nothing about removing a necessary clue. In fact, he then defines a valid puzzle as
Nobody asked me, but I suggest,

coloin wrote:grid = 81 clue valid grid solution - maximally completed puzzle.
Okay, I'm with you here.
coloin wrote:subgrid - a grid with some n clues removed - but still 1 solution - [if some clues are superfluos - non-minimal "puzzle" ]
I didn't see this in JPF's definition. I would have called this a valid puzzle (or a sudoku).
coloin wrote:subpuzzle - a valid puzzle with a necessary clue[s] removed - therefore more than 1 grid solution
Here is where my confusion starts. JPF defines a subpuzzle as
JPF wrote:subpuzzle : a grid in which some digits have been removed.
It says nothing about removing a necessary clue. In fact, he then defines a valid puzzle as
JPF wrote:valid Puzzle : a subpuzzle with a unique solution.
Nobody asked me, but I suggest,
- grid: a full Sudoku grid (9x9) with a digit in each cell, 9 different digits in each unit.
- subgrid: a subset of grid (note this is no longer, in general, a 9x9 matrix, just a collection of cells with digits)
- puzzle: a grid with digits removed from some cells (note that this is still a 9x9 grid, but without digits in some cells). One might say that you contract a grid (or a puzzle) to a puzzle.
- solution of a puzzle: A grid consistent with the puzzle. One might say that you complete a puzzle to a grid.
- valid puzzle or sudoku: A puzzle with a unique solution (i.e., a unique completion).
- minimal puzzle: A valid puzzle such that every contraction has more than one solution.
- subpuzzle: A subset of a puzzle. In other words, a subpuzzle is the intersection of the puzzle with a subgrid of any solution of the puzzle.
- re'born
- Posts: 551
- Joined: 31 May 2007
Allan Barker wrote:The term Isolated Sub-Puzzles evolved from the other thread.
[...]
First image, a standard UR. Left: one of 27 possible continuous nice loops, only 4 are required to clear the region. Note: colored bars are strong sets and white bars are linksets. Right. An isolated UR region with all of its 16 sets. At this point, they are all strong links.
Allan, thanks for the illustrations. I now see why my suggestion of "independent" subpuzzles made no sense to you.
I was mentally picturing at least two subpuzzles: 1) at least one "non-uniqueness pattern", and 2) whatever is leftover. These subpuzzles are all mutually independent, i.e., no one subpuzzle exerts any influence over the other.
It's the lack of this mutual independence that creates RW's UR1.1 pattern.
[edit: later per Myth Jellies, UR1.1 attributed to RW]
Last edited by ronk on Thu Nov 13, 2008 2:31 pm, edited 1 time in total.
- ronk
- 2012 Supporter
- Posts: 4764
- Joined: 02 November 2005
- Location: Southeastern USA
Indeed re'born.........
As long as evreybody uses the same words to describe the same things
The word "grid" has long been used interchangeably and with much confusion to mean "solution grid" or "puzzle".
When you assume uniqueness.......a puzzle is a "puzzle" and has a valid unique soltion. And it defines or contracts a grid solution.
I suppose I feel that a subpuzzle "should" have more than 1 solution.......otherwise if it has 1 solution we have the situation where a subpuzzle is still actually a puzzle !
The pencilmarks problem you get with these "subpuzzles with more than 1 solution" [grrr] has yet to be commented on...but I suspect it might now be completely different from AB and DPBs discussion, which I will now study...
As long as evreybody uses the same words to describe the same things
The word "grid" has long been used interchangeably and with much confusion to mean "solution grid" or "puzzle".
When you assume uniqueness.......a puzzle is a "puzzle" and has a valid unique soltion. And it defines or contracts a grid solution.
I suppose I feel that a subpuzzle "should" have more than 1 solution.......otherwise if it has 1 solution we have the situation where a subpuzzle is still actually a puzzle !
The pencilmarks problem you get with these "subpuzzles with more than 1 solution" [grrr] has yet to be commented on...but I suspect it might now be completely different from AB and DPBs discussion, which I will now study...
- coloin
- Posts: 2664
- Joined: 05 May 2005
- Location: Devon
Is the following what's meant by "isolated subpuzzle" ...
(Assumption: the original puzzle has >0 solutions.)
ISP if and only if:
(Assumption: the original puzzle has >0 solutions.)
ISP if and only if:
- it's a set of cells, C, and all the candidates within them;
- for each unit (row, column or box) of the grid, there are as many different cells in C as there are candidate-values in C.
- Red Ed
- Posts: 633
- Joined: 06 June 2005
Here's a pretty trivial proof, conditional upon me having understood what Allan was getting at.
"If": if there are n different values to place in n C-cells (of some row, column or box) then clearly they must all be placed in those C-cells and not outside. In other words, those candidates are cleared from outside of C.
"Only if": if there are N>n different values to place in n C-cells (of some row, column or box) then clearly one of them must be placed outside. In other words, one of them is not cleared from outside of C.
Note that there can never be m<n different values to place in n C-cells (of some row, column or box), since that would mean at least one was duplicated - contradicting the assumption that the puzzle had >0 solutions.
"If": if there are n different values to place in n C-cells (of some row, column or box) then clearly they must all be placed in those C-cells and not outside. In other words, those candidates are cleared from outside of C.
"Only if": if there are N>n different values to place in n C-cells (of some row, column or box) then clearly one of them must be placed outside. In other words, one of them is not cleared from outside of C.
Note that there can never be m<n different values to place in n C-cells (of some row, column or box), since that would mean at least one was duplicated - contradicting the assumption that the puzzle had >0 solutions.
- Red Ed
- Posts: 633
- Joined: 06 June 2005
Another quick observation, conditional upon my understanding of "ISP" being correct:
- All (uniqueness) deadly patterns are ISPs.
- Not all ISPs are deadly patterns (for example: any collection of solved cells is an ISP).
- Red Ed
- Posts: 633
- Joined: 06 June 2005

