The New Sudoku Players' Forum

[urhegyi]

2020-11-20 (8).png (87.78 KiB) Viewed 573 times

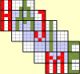
Till now all eliminations were generalized intersections. Now comes the tricky part. There are a few candidates not eliminated on the picture because the program didn't support diagonal blocks. There are 2 possible placements for the candidate 8 at column 4, at row 2 (or nonet 1) or at row 8 (or nonet 8). I think here I have to find a chain to find the right one. When I take the one at R2C4, puzzle solves with a couple of x and xy-wings.

[Hajime]

Looks great. You, SumoCue and Sudoku Jigsaw Explainer can solve the SiSeSuSo puzzles.
Maybe I should not have the symmetrical layout, to make it harder.

[1to9only]

the program didn't support diagonal blocks.

I've updated the SudokuJigsawExplainer that now supports X - download from: https://github.com/1to9only/SudokuJigsawExplainer/releases
The program should work fine, but note that I have not tested all features!

Some examples:

11-clues: Easy - ED=2.8/1.2/1.2

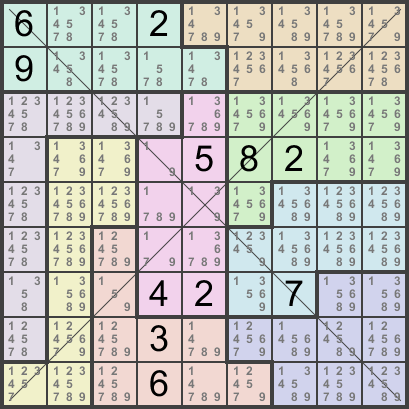
Code: Select all

6..2.....9.....................582.......................42.7.....3........6..... 111122222111112222333345555366445555366445777368447777368447799368889999668888999 JSX

SumoCueV1D=6J0=0J0=0J0=2J0=0J1=0J1=0J1=0J1=0J1=9J0=0J0=0J0=0J0=0J0=0J1=0J1=0J1=0J1=0J2=0J2=0J2=0J2=0J3=0J4=0J4=0J4=0J4=0J2=0J5=0J5=0J3=5J3=8J4=2J4=0J4=0J4=0J2=0J5=0J5=0J3=0J3=0J4=0J6=0J6=0J6=0J2=0J5=0J7=0J3=0J3=0J6=0J6=0J6=0J6=0J2=0J5=0J7=4J3=2J3=0J6=7J6=0J8=0J8=0J2=0J5=0J7=3J7=0J7=0J8=0J8=0J8=0J8=0J5=0J5=0J7=6J7=0J7=0J7=0J8=0J8=0J8


17-clues: Hard - ED=4.0/4.0/2.6

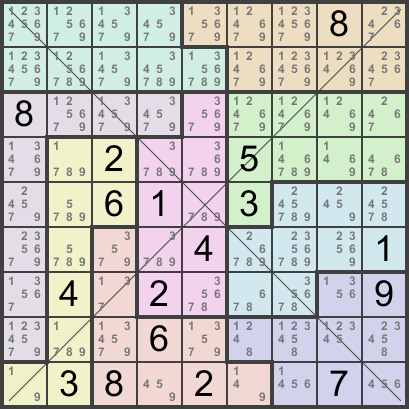
Code: Select all

.......8..........8..........2..5.....61.3.......4...1.4.2....9...6......38.2..7. 111122222111112222333345555366445555366445777368447777368447799368889999668888999 JSX

SumoCueV1D=0J0=0J0=0J0=0J0=0J1=0J1=0J1=8J1=0J1=0J0=0J0=0J0=0J0=0J0=0J1=0J1=0J1=0J1=8J2=0J2=0J2=0J2=0J3=0J4=0J4=0J4=0J4=0J2=0J5=2J5=0J3=0J3=5J4=0J4=0J4=0J4=0J2=0J5=6J5=1J3=0J3=3J4=0J6=0J6=0J6=0J2=0J5=0J7=0J3=4J3=0J6=0J6=0J6=1J6=0J2=4J5=0J7=2J3=0J3=0J6=0J6=0J8=9J8=0J2=0J5=0J7=6J7=0J7=0J8=0J8=0J8=0J8=0J5=3J5=8J7=0J7=2J7=0J7=0J8=7J8=0J8


12-clues: Highest rated - ED=11.3/1.2/1.2

Code: Select all

..5...37..3..9...........8................4.....9.............2...1.....7.......1 111122222111112222333345555366445555366445777368447777368447799368889999668888999 JSX

SumoCueV1D=0J0=0J0=5J0=0J0=0J1=0J1=3J1=7J1=0J1=0J0=3J0=0J0=0J0=9J0=0J1=0J1=0J1=0J1=0J2=0J2=0J2=0J2=0J3=0J4=0J4=8J4=0J4=0J2=0J5=0J5=0J3=0J3=0J4=0J4=0J4=0J4=0J2=0J5=0J5=0J3=0J3=0J4=4J6=0J6=0J6=0J2=0J5=0J7=9J3=0J3=0J6=0J6=0J6=0J6=0J2=0J5=0J7=0J3=0J3=0J6=0J6=0J8=2J8=0J2=0J5=0J7=1J7=0J7=0J8=0J8=0J8=0J8=7J5=0J5=0J7=0J7=0J7=0J7=0J8=0J8=1J8


JigsawExplainer can also generate other JSX, or even JSBX (I've not tried this!).

Moonlotus: Medium - ED=2.9/1.2/1.2

Code: Select all

2..5.4.1...9.1............9........8.1.....2.8........6............3.6...7.6.9..4 112222233111222333411123335441666355444666555447666855477798885777999888779999988 JSX

SumoCueV1D=2J0=0J0=0J1=5J1=0J1=4J1=0J1=1J2=0J2=0J0=0J0=9J0=0J1=1J1=0J1=0J2=0J2=0J2=0J3=0J0=0J0=0J0=0J1=0J2=0J2=0J2=9J4=0J3=0J3=0J0=0J5=0J5=0J5=0J2=0J4=8J4=0J3=1J3=0J3=0J5=0J5=0J5=0J4=2J4=0J4=8J3=0J3=0J6=0J5=0J5=0J5=0J7=0J4=0J4=6J3=0J6=0J6=0J6=0J8=0J7=0J7=0J7=0J4=0J6=0J6=0J6=0J8=3J8=0J8=6J7=0J7=0J7=0J6=7J6=0J8=6J8=0J8=9J8=0J8=0J7=4J7


[urhegyi]

2020-11-20 (8).png (87.78 KiB) Viewed 548 times

Till now all eliminations were generalized intersections. Now comes the tricky part. There are a few candidates not eliminated on the picture because the program didn't support diagonal blocks. There are 2 possible placements for the candidate 8 at column 4, at row 2 (or nonet 1) or at row 8 (or nonet 8). I think here I have to find a chain to find the right one. When I take the one at R2C4, puzzle solves with a couple of x and xy-wings.

Now I understand generalized intersections better:R5C68 are the only 2 candidates for 3 in the row.if R5C6=3 or R5C8=3 in both cases ==> R4C8<>3. Now one of the candidates at R45C6 has to be 3 because there has to be a 3 in the nonet. So the other 3's at the column 6 outside the nonet R68C6 <>3. R4C4<>2 because of R2C2=2 on the diagonal. There are two possible placements of candidate 8 at column 4 at R28C4. Suppose R8C4=8 then R5C4=2 and R5C6=1 and R6C6=5 and R8C6=8 so R8C4 can't be 8 and R2C4 must be 8. Now solvable with singles.

You need some chains...

As you can see this solution is based on a forcing(contradiction) chain. When you created the puzzle did you have a solution with xy-chain(bivalue chain) in your mind? What solution finds your SiSeSuSo solver? I'm curious to know...