The 2 eyes form 2 blocks containing the digits 1 to 9 only one time. The same goes for the mouth which is also an extra block containing the digits 1 to 9 only once.
I already solved it half with logic and trial and error for the other part because i didn't found the way to start. Any advice?
Halloween Sudoku
11 posts
• Page 1 of 1
Halloween Sudoku
- Attachments
-
- 121642142_10158900859554923_2059651658671508700_n.jpg (12.93 KiB) Viewed 1601 times
- urhegyi
- Posts: 763
- Joined: 13 April 2020
Re: Halloween Sudoku
I solved the puzzle and it seemed quite straightforward, so it's difficult to guess where you might be stuck. Could you post the exact point in the puzzle that you are stuck on? It will be easier for us to help then.
- SCLT
- Posts: 171
- Joined: 06 August 2013
Re: Halloween Sudoku
SCLT wrote:I solved the puzzle and it seemed quite straightforward, so it's difficult to guess where you might be stuck. Could you post the exact point in the puzzle that you are stuck on? It will be easier for us to help then.
I redid my steps from the notes I took, and actually the second time it's much easier. At this point it seemed already been solved:
- urhegyi
- Posts: 763
- Joined: 13 April 2020
Re: Halloween Sudoku
Singles only, most hidden singles, some naked singles, easy but a pretty nice puzzle !
A possible solution path:
A possible solution path:
Hidden Text: Show
-

Hajime - Posts: 1427
- Joined: 20 April 2018
- Location: Fryslân
Re: Halloween Sudoku
I set it up on Hodoku - first color the cells for the eyes and mouth, File -> Modify Givens to set givens, File -> Play Game when ready.
The eyes and mouth regions have to be manually checked for candidates eliminations.
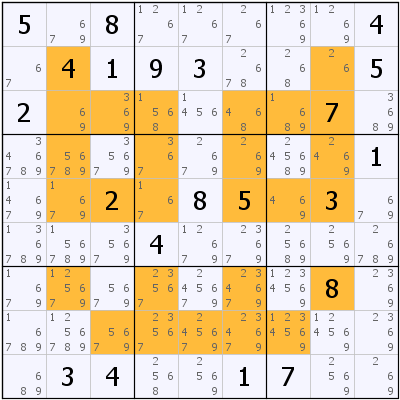
As noted in a previous post, the puzzle solves with singles only, ED=1.5/1.2/1.2.
The eyes and mouth regions have to be manually checked for candidates eliminations.

As noted in a previous post, the puzzle solves with singles only, ED=1.5/1.2/1.2.
-

1to9only - Posts: 4211
- Joined: 04 April 2018
Re: Halloween Sudoku
I generated a few of the halloween sudokus to keep busy before halloween day!
[Edit 22/10] Solutions - the ED ratings may be slightly different as I've now added Intersections for this variant!
- Code: Select all
........9..8...4.5.....8..........7.3...82.....7..42.........1...93.....5.....8.. ED=1.5/1.2/1.2
.....7.12.6.....3..24.9......8..1..........5..4...6.2........4.......7.....2..... ED=1.5/1.2/1.2
.........69......2.....5.1.4.3.86.............1....7.......32.....5....3..5...... ED=1.5/1.2/1.2
.9..82...7..6.....2....1............9..1...........8.4..3....2.......18..5......6 ED=1.5/1.5/1.5
...7.......3..5..281...6.5.......37496........................6.....8.35......... ED=2.0/1.2/1.2
9.......3..2...14.........2..........3............9.7..8.195.............2.46..1. ED=3.4/1.2/1.2
..7...........3..7....6.8..1.3.........5.4....4........2.3..75.5.86.............. ED=3.8/1.2/1.2
..4.6..........26...79.....3.........1...784.............61.4.........58.......3. ED=4.2/1.2/1.2
.......9..5..1.42....8.....3..7.1..8..2....5........6....5..28............3...... ED=4.4/1.2/1.2
......2.........6...45...91...6.2..8...1...5...6.87.......2.9...1......3......... ED=4.4/1.2/1.2
[Edit 22/10] Solutions - the ED ratings may be slightly different as I've now added Intersections for this variant!
Hidden Text: Show
Last edited by 1to9only on Thu Oct 22, 2020 8:41 am, edited 1 time in total.
-

1to9only - Posts: 4211
- Joined: 04 April 2018
Re: Halloween Sudoku
Nice job creating 10 more Halloween sudokus. I read about windoku last week with 9 possible blocks:
9 5 5 5 9 6 6 6 9
7 1 1 1 7 2 2 2 7
7 1 1 1 7 2 2 2 7
7 1 1 1 7 2 2 2 7
9 5 5 5 9 6 6 6 9
8 3 3 3 8 4 4 4 8
8 3 3 3 8 4 4 4 8
8 3 3 3 8 4 4 4 8
9 5 5 5 9 6 6 6 9
Is there some similarity when defining Halloween sudokus?
9 5 5 5 9 6 6 6 9
7 1 1 1 7 2 2 2 7
7 1 1 1 7 2 2 2 7
7 1 1 1 7 2 2 2 7
9 5 5 5 9 6 6 6 9
8 3 3 3 8 4 4 4 8
8 3 3 3 8 4 4 4 8
8 3 3 3 8 4 4 4 8
9 5 5 5 9 6 6 6 9
Is there some similarity when defining Halloween sudokus?
- urhegyi
- Posts: 763
- Joined: 13 April 2020
Re: Halloween Sudoku
Only a very small similarity: the bottom 3 blocks contain the mouth, so there must be exactly 2 digits 1to9 in the white.
-

Hajime - Posts: 1427
- Joined: 20 April 2018
- Location: Fryslân
Re: Halloween Sudoku
urhegyi wrote:Nice job creating 10 more Halloween sudokus. I read about windoku last week with 9 possible blocks:
9 5 5 5 9 6 6 6 9
7 1 1 1 7 2 2 2 7
7 1 1 1 7 2 2 2 7
7 1 1 1 7 2 2 2 7
9 5 5 5 9 6 6 6 9
8 3 3 3 8 4 4 4 8
8 3 3 3 8 4 4 4 8
8 3 3 3 8 4 4 4 8
9 5 5 5 9 6 6 6 9
Is there some similarity when defining Halloween sudokus?
Yes there are (29 easy) hidden constraints but usefulness is always limited.
Can sometimes skip complicated steps in special designed puzzles. Not as useful compared with windoku.
- creint
- Posts: 402
- Joined: 20 January 2018
Latin Square + Halloween
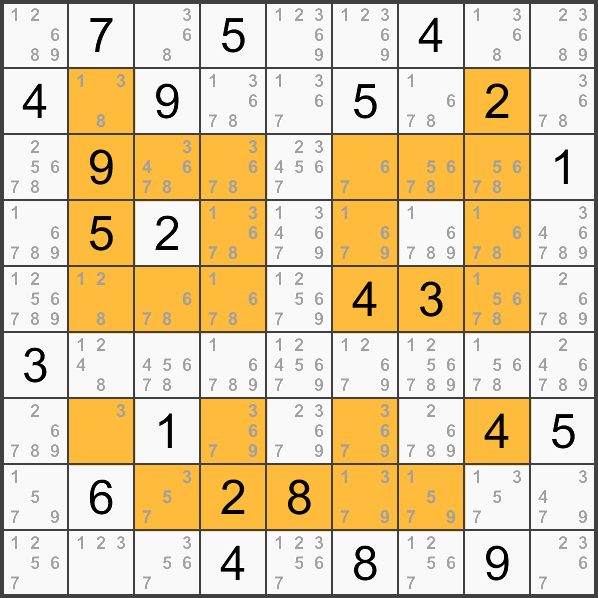
This has no 3x3 blocks - difficulty: easy
- Code: Select all
.7.5..4..4.9..5.2..9......1.52...........43..3..........1....45.6.28.......4.8.9. ED=2.0/1.5/1.5
Solution:
Hidden Text: Show
-

1to9only - Posts: 4211
- Joined: 04 April 2018
Re: Halloween Sudoku
Another Halloween Sudoku, symmetric, with boxes and 4 extra regions, easy, singles only:

More difficult ones, also symmetric, with same layout (moderate, hard and extreme):

- Code: Select all
#1/JSB/B4
9..5.2..3.56...41...3...5...............................2...7...37...92.6..7.1..4
.........1111.2222.111.222...11.22..3.......43.3...4.43333.4444.3.3.4.4..........
More difficult ones, also symmetric, with same layout (moderate, hard and extreme):
- Code: Select all
#1/JSB/B4
.2.9.8.4.....5.............6.......7.7.4.1.6.1.......4...3.9.....8.4.3...........
.........1111.2222.111.222...11.22..3.......43.3...4.43333.4444.3.3.4.4..........
#1/JSB/B4
9.67.21.4.........7.......9....8......9...8......7....5.......2.........4.82.73.5
.........1111.2222.111.222...11.22..3.......43.3...4.43333.4444.3.3.4.4..........
#1/JSB/B4
....4.....7.1.8.9.............5.4.....17.38..7..9.6..3.1.....7..............7....
.........1111.2222.111.222...11.22..3.......43.3...4.43333.4444.3.3.4.4..........
-

Hajime - Posts: 1427
- Joined: 20 April 2018
- Location: Fryslân
11 posts
• Page 1 of 1

