The New Sudoku Players' Forum

by **Allan Barker** » Sat Oct 25, 2008 6:03 am

Great Monster Loops

I just came across Obi-Wahn's list of hardest multiple jelly puzzles in the Hardest Sudokus thread here and took a look at the first puzzle:
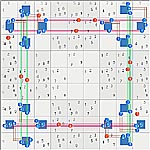
Coloin-04/13-1414, which is rated at 11.8 on the SER scale. This puzzle has two different initial high symmetry loops, one of which is similar to SteveK's original SK loop from Easter Monster. The other is about the same size, more complex structurally, and wipes out 19 candidates almost solving the puzzle. Both loops are shown below.

As additional loops reveal their diverse logical nature, it becomes clear that the original SK loop is one of a number of possible logic structures, many of which are more complex, and can be harder to find. To see this, I have compared 10 loops from 6 puzzles, including Fata Morgana, Easter Monster, Tungsten Rod, Strmckr's Puzzle, and Golden nugget. Golden Nugget is included because its morphed symmetrical form, here has similar kinds of loops.

The table below summarizes several loop properties. The puzzles are listed in order of different kinds of complexity found in the loops. Properties include the presence of bi-value sets, the number of each type of set used, number of candidates removed, and the logic rank. Rank 0, fish like logic, is common but several loops have mixed rank logic that promotes some of the links to rank 0. Core refers loops with additional logic in the center box. The loops have other logical properties, not listed, such as symmetric or anti-symmetric digit layers, and layers that have the same or different logic. It's possible these loops are just part of an entire family of logical structures, just like fish.

I have added a new page to my website: Inside the Great Monsters,

that compares all 10 loops, where I also try to capture some of the natural beauty of Sudoku logic. While spatial symmetries must be 4-fold, some of these loops show 3-fold logical symmetries that can be either symmetric or anti-symmetric.

As more loops are uncovered, I will add them to this summary information, and provide additional links to data.

Summary Table

Code: Select all: ------ strong sets -------- remaining 2-value 3-value 4/5-value core logic elim. difficulty Fata Morgana loop-1 --- 8 3 yes rank 0,1 2 Fata Morgana loop-2 --- 14 - yes rank 0,1 6 medium Golden Nugget (morph) 1 10 6 yes rank 0,1 1 hard Tungsten Rod 1 6 2 yes rank 1 2 medium Coloin-04/13-1414 loop-1 4 11 2 yes rank 0 19 easy Coloin-04/13-1414 loop-2 2 10 4 no rank 0 14 Coloin-04/13-1414 loop-3 02 16 4 no rank 0 14 Easter Monster 4 12 - no rank 0 13 hard StrmCkr's Puzzle loop-1A 4 12 - no rank 0 9 StrmCkr's Puzzle loop-1B --- --- 12 no rank 0 9 StrmCkr's Puzzle move 2 --- 4 4 yes rank 0 12 v. hard

Coloin-04/13-1414 loop-1

Note: all cordinates are in NRC format (digit, row, column), = strong link, | weak link. Targets and not included in the logic-grams below for clarity, but are in the 2D grid images at the bootom, and in the set logic listing.

Code: Select all: COL1 51 Nodes, Rank 0: Removes 19 Candidates 17 Sets = {167r2 167r8 1267c2 1267c8 5n6 2b28} 17 Links = {2r3 127r5 2r9 2n56 4n8 6n2 8n45 7b1 16b3 16b7 7b9} --> (7b1) => r1c3<>7, (2n5) => r2c5<>3, (2n5) => r2c5<>8, (2n6) => r2c6<>3, (2r3) => r3c1<>2, (4n8) => r4c8<>9, (2r5) => r5c1<>2, (1r5) => r5c3<>1, (7r5) => r5c3<>7, (1r5) => r5c4<>1, (2r5) => r5c4<>2, (7r5) => r5c4<>7, (1r5) => r5c7<>1, (2r5) => r5c7<>2, (7r5) => r5c9<>7, (7b9) => r7c9<>7, (8n4) => r8c4<>5, (8n5) => r8c5<>4, (2r9) => r9c7<>2 1R8: 185==184============183 | | | 1C2: | | 172=======162============152 | | | | 1C8: | | | 158==148============138 | | | | | | 1R2: | | | | | 127=======126==125 2B8: 285==284=======294 | | | | | | | 295 | | | | | | | 296 | | | | | | | | | | | | | 2C8: | | 298=============|========258===|===248 | | | | | | | | | | 5N6: | | | 756==256==156 | | | } Central core set | | | | | | | | 2C2: | | 262===|===252========|========232 | | | | | | | | | | 2B2: | | | | | 234============226==225 | | | | | 235 | | 6R8: | 684=================681 | | | | | | | | | | | | | } 6C2: | | 692==662 | | | | } Bi-value 6C8: | | | | 648==618 | | } sets layer | | | | | | | | } 6R2: | | | | | 629=================626 | } 7R8: 785==784==789 | | | | | | | | | | | 7C2: | 762==752=============|==================712 | | | | | | | | 7R2: | | | 723==726==725 7C8: 778======================758============748

Coloin-04/13-1414 loop-2

Code: Select all: COL2 54 Nodes, Rank 0: Removes 14 candidates 16 Sets = {1r28 2r28 6r2468 17c2 17c8 2b46 7b28} 16 Links = {7r17 26c1 2c7 6c9 2n56 4n8 5n28 6n2 8n45 1b37} --> (7r1) => r1c3<>7, (2n5) => r2c5<>3, (2n5) => r2c5<>8, (2n6) => r2c6<>3, (2c1) => r3c1<>2, (4n8) => r4c8<>9, (5n2) => r5c2<>4, (5n2) => r5c2<>8, (5n8) => r5c8<>3, (5n8) => r5c8<>9, (7r7) => r7c9<>7, (8n4) => r8c4<>5, (8n5) => r8c5<>4, (2c7) => r9c7<>2 7B2: 726=======725===============================================714 | | 715 | | 716 2R2: 226=======225==========================================221 | | | | | 1R2: 126==127==125 | | 7C2: | | | 712==752=======762 | | | | | 2B4: | | 241=======252=======262 | | 251 | | | | 261 | | 1C2: | | 152==172==162 2R8: | | 287============284==285 | | | | | | | | | 7B8: | | | 774=======784==785 | | | | | 775 | | | | | | | 776 | | | | | | | | | | | | 2B6: | | 258==248=======247 | | | | | | | | | 257 | | | | | | | | | 267 | | | | | | | | | | | | | | 7C8: | | 758==748============778 | | | | 1R8: | | | | 184==185=================183 | | | | | | | 6R8: | | | | 681==684 | | | | | | | 6R6: | | | | 669============661================================662 | | | | | | 6R4: | | | 648==649============641 | | | | | 1C8: | 138=======158==148 | | | 6R2: 626======================629

Coloin-04/13-1414 loop-3, classic SK type

Code: Select all: COL3 48 Nodes, Rank 0: 16 Sets = {1n28 2n1379 3n28 7n28 8n1379 9n28} 16 Links = {38r2 45r8 48c2 39c8 27b1 16b3 16b7 27b9} --> (7b1) => r1c3<>7, (3r2) => r2c5<>3, (8r2) => r2c5<>8, (3r2) => r2c6<>3, (2b1) => r3c1<>2, (9c8) => r4c8<>9, (4c2) => r5c2<>4, (8c2) => r5c2<>8, (3c8) => r5c8<>3, (9c8) => r5c8<>9, (7b9) => r7c9<>7, (5r8) => r8c4<>5, (4r8) => r8c5<>4, (2b9) => r9c7<>2 7N2: 472==872===================================================================172 | | | 9N2: 492==892==============================================================692 | | | | | 3N2: 432==832=======232 | | | | | | | 1N2: 412==812==712 | | | 2N1: | 221==321==821 | | | | | | | 2N3: 723=======323==823 | | | | | | 2N9: 329==829=======629 | | | | | | | 2N7: 327==827==127 | | | 1N8: | 618==318==918 | | | | | | | 3N8: 138=======338==938 | | | | | | 7N8: 378==978=======778 | | | | | | | 9N8: 398==998==298 | | | 8N1: | | 481==581==681 | | | | | | 8N3: | | 483==583=======183 | | | | 8N9: | 789==489==589 | | | 8N7: 287=======487==587

Thumbs to images: left to right loop COL1, COL2, COL3.

,

Edit: Added loop COL3, suggested by Ronk. 2) fixed broken link to website 3) removed statement concerning methodologies

by **ronk** » Sat Oct 25, 2008 6:35 am

Allan, very nice as usual. If you find the time, would you please post an alternate 2-D image for COL2 using ...

sets = {r28c1379, r1379c28} :?:

TIA, Ron

[edit: deleted comment which became an excuse for off-topic discussion]

Website · by **denis_berthier** » Sat Oct 25, 2008 7:07 am

ronk wrote:
Allan Barker wrote:This thread is completely T&E free

I get it, I get it.

I must be very stupid, but I don't get it.
Can any one of you two explain?

by **Allan Barker** » Sat Oct 25, 2008 7:25 am

ronk wrote:If you find the time, would you please post an alternate 2-D image for COL2 using ...

sets = {r28c1379, r1379c28} TIA, Ron

Ronk, nice shot. It eliminates the same 14 candidates as COL2 it has the classic layout for an SK loop. However, it's another example of a loop with no bi-value sets, which may contribute to the puzzle's high rating?

Will post the image soon.

by **ronk** » Sat Oct 25, 2008 7:58 am

edit: deleted post which fed an off-topic discussion

Website · by **denis_berthier** » Sat Oct 25, 2008 8:34 am

ronk wrote:Since there is no preselected target and no directionality -- except possibly to "transport rank" when rank>0 -- it's unlikely anyone will claim Allan's "constraint sets" method to be T&E, even me.

No resolution rule has a preselected target. Targets are selected in the same way as the pattern: they have to match the conditions. In this respect, Allan does exactly the same thing for his targets as I do for mine.

"No directionality" - another name for Myth's controversial and never defined reversibility - has nothing to do with T&E. It is nothing more than one of the prejudices of the AIC community.
Directionality of the nrczt-chains, since this is what you're speaking of, is the source of their great resolution potential - with no need for patterns of rank > 1.

ronk wrote:Unfortunately, as the number of set members increases, the method quickly falls beyond the capability of human solvers.

It is equally true that:
- as the size of the ALSs increases, AICs quickly fall beyond the capability of human solvers
- as the length of the nrczt-whips increases, they quickly fall beyond the capability of human solvers

Allan has nevertheless found very interesting loop patterns. No matter how he found them, with or without a computer: they are there for everyone to see them.

by **Allan Barker** » Sat Oct 25, 2008 9:44 am

Denis B. wrote:Can any one of you two explain?

I make the comment because it may not be clear that I am solving many of these monsters without any T&E at all, e.g, someone who joined just recently claimed (opined) that all Sudoku methods use T&E. It has also been mentioned in a few places that attitudes towards T&E have been changing, including your recent work on braids. So, considering all that, considering the subject of this thread, it seems a good time and place to point out that my set methods do not use T&E.

As far as my own take on T&E, to me the problem is it may not provide a useful logical form, which is why I was curious about your thoughts on extracting useful logical information from processes that use T&E. I personally think this is an interesting subject.

by **David P Bird** » Sun Oct 26, 2008 2:50 am

Allan to respond to your sideswipe: we deprecate trial and error as being brainless and inefficient. However in comparison to massaging the data map in an extensive number of ways in the hope of finding an exclusion pattern, the effort and the number of trials involved can be considerably less. It boils down to how you compare the outcome of an erroneous assumption with the failure to find a reduction pattern, and how you suppose the processes were conducted. I hold it's not so clear cut as you seem to think.

However that said, starting from a two-sided conjugate premise, all the inferences we derive from AICs are coherent and will persist through to the final solution, so if they aren't immediately useful, they may be later. This gives them a far higher utility value than single sided assumptions or unidirectional chains for the manual solver which is the direction I come from.

Recently I wondered why I never seemed to find any Sue de Coq patterns when I looked for them. The answer was because I'd already found the eliminations using ALSs in AICs. A SdC when it occurs is elegant and powerful, but if we fail to find the pattern we've got little in the way of information to use in the rest of our solving process, so I don't look for them at all now, but reserve the option to reverse engineer one if I spot the overlap. I wonder what your approach would be?

Website · by **denis_berthier** » Sun Oct 26, 2008 3:58 am

Allan Barker wrote:As far as my own take on T&E, to me the problem is it may not provide a useful logical form, which is why I was curious about your thoughts on extracting useful logical information from processes that use T&E. I personally think this is an interesting subject.

First, you must remember that the T&E I'm speaking of is the T&E usual in Sudoku: no guessing, no recursion.

I explained this construction here for nrczt-braids: http://forum.enjoysudoku.com/viewtopic.php?t=5591&postdays=0&postorder=asc&start=150.
The proof of the T&E vs braid theorem shows how a braid can be constructed from the trace of a T&E procedure.
This can easily be extended to any zt-braid(FP) for any family FP of patterns.

Said otherwise, for any family FP of patterns such that T&E(FP) solves a puzzle P, one can build a solution pf P with zt-braids(FP).

But, there are two major differences between such a solution built indirectly via the T&E procedure and one built by searching directly for the braid patterns:
- you won't find the shortest braids,
- you won't find whips (or even simpler patterns) instead of braids when those are enough to solve the puzzle; indeed, you have no control on what you'll find.

I'd say the hallmark of T&E is the absence of control over the patterns found (size, type, ...)

by **champagne** » Sun Oct 26, 2008 7:07 am

Great Monster Loops

I just came across Obi-Wahn's list of hardest multiple jelly puzzles in the Hardest Sudokus thread here and took a look at the first puzzle:
Coloin-04/13-1414, which is rated at 11.8 on the SER scale. This puzzle has two different initial high symmetry loops, one of which is similar to SteveK's original SK loop from Easter Monster. The other is about the same size, more complex structurally, and wipes out 19 candidates almost solving the puzzle. Both loops are shown below.

Hi Allan,

Unless I made a mistake, all these puzzles except one (from tarek) have the SK loop.

Seen by my solver, tarek's puzzle is by far the toughest in that lot. Would be in the bottom part of my own list of hardests.

by **Allan Barker** » Sun Oct 26, 2008 7:09 am

David,

For sure, no sideswipe or depreciation of trial and error was meant. The only intended meaning are the words as written, that the processes used to solve these puzzles do not rely on trial and error. The reason for the statement is that it might be assumed these methods do use some form of trial and error to overcome the extreme difficulty of the puzzles. The form of the comment is meant to be friendy. Like they say, if I sideswiped anyone, it was while I was sleeping in my car on the side of the road. But I suppose I should move the car?

Anyway, I don't think I have ever discussed TE, outside what I mentioned just above, where I think it would interesting to obtain logical information (like eliminations) from processes like Algorithm-X, but don't yet know how to do it. This is in line with your comment about extensive data map massaging.

DPB wrote:starting from a two-sided conjugate premise, all the inferences we derive from AICs are coherent and will persist through to the final solution, so if they aren't immediately useful, they may be later

I don't think of this as trial and error. For me, TE methods are what I call grid solvers that quickly provide a solution without the logical eliminations that we normally work with.

DPB wrote:Recently I wondered why I never seemed to find any Sue de Coq patterns when I looked for them. The answer was because I'd already found the eliminations using ALSs in AICs. A SdC when it occurs is elegant and powerful, but if we fail to find the pattern we've got little in the way of information to use in the rest of our solving process, so I don't look for them at all now, but reserve the option to reverse engineer one if I spot the overlap. I wonder what your approach would be?

I often solve puzzles using my software as a manual graphical finder's tool. It will find a Sue de Coq if it is a reasonable choice for that grid but they seem quite rare. I have found a couple.

by **Allan Barker** » Sun Oct 26, 2008 7:13 am

Ronk wrote:Since there is no preselected target and no directionality -- except possibly to "transport rank"

Denis B. wrote:No resolution rule has a preselected target. Targets are selected in the same way as the pattern: they have to match the conditions. In this respect, Allan does exactly the same thing for his targets as I do for mine.

Denis, yes, I imagine this is pretty much the same.

Ronk's idea of rank transport helps to see how a set approach may differ. As a (pure simple) chain propagates, it transports along its length the logical inferences required to eliminate a candidate. A set approach propagates throughout an area by transporting local area rank information required to eliminate candidates.

To me, the nrctz approach sits somewhere inbetween. While maintaining linear control over the search, it is able to examine the local area for information that helps to propogate the logic further.

by **Allan Barker** » Sun Oct 26, 2008 7:46 am

Hi Champagne,

champagne wrote:Unless I made a mistake, all these puzzles except one (from tarek) have the SK loop.

Seen by my solver, tarek's puzzle is by far the toughest in that lot. Would be in the bottom part of my own list of hardests.

The idea here is to gather and visualize different types of loop structures from difficult puzzles. I also imagine that one puzzle may have different types of loops. If you have puzzles you think might have interesting loop structures you could psot them here and we could study them.

I could find a loop in GN but only after morphing the puzzle, then it was very different from more common loops like the original SK loop. Have you seen other loops ofr GN?

by **champagne** » Sun Oct 26, 2008 8:09 am

Allan Barker wrote:The idea here is to gather and visualize different types of loop structures from difficult puzzles.

I understand that. I see several problems with the SK loop (strictly defined as a loop of AC2 structures)

. It is very easy to detect for a player, so your process has no added value in the first phase. What can happen just after the SK loop clearing is more interesting

. it should lead to very similar loop structures,

. It is a very specific family of puzzles.

Normally a sample file including 2 or 3 puzzles having the SK loop should be enough.

Allan Barker wrote:If you have puzzles you think might have interesting loop structures you could spot them here and we could study them.

I know your process often turns to loops diagrams. This is not at alll the way AIC's nets are solving puzzles, so it is difficult to tell whether a puzzle will show up with something interesting for you.

What I can do is a kind of preprocessing of my list of hard puzzles and extract those offering a multi floors promising pattern.

Allan Barker wrote:I could find a loop in GN but only after morphing the puzzle, then it was very different from more common loops like the original SK loop. Have you seen other loops ofr GN?

I am not surprised that you faced problems with that one. I am afraid all my top list will create similar difficulties.

I launch anyway my test very quickly.

champagne

by **champagne** » Sun Oct 26, 2008 8:35 am

Hi again Allan,

Here, what tells me the solver for the three puzzles at the top of my list of hardest (including Golden Nugget, number 3)

Code: Select all: 100000007020400060003000500090040000000062040000900800005000003060200080700001000 Silver Plate

Code: Select all: 1 458 4689 |3568 23589 35689 |2349 239 7 589 2 789 |4 135789 35789 |139 6 189 4689 478 3 |1678 12789 6789 |5 129 12489 --------------------------------------------------------- 23568 9 12678 |13578 4 3578 |12367 12357 1256 358 13578 178 |13578 6 2 |1379 4 159 23456 13457 12467 |9 1357 357 |8 12357 1256 --------------------------------------------------------- 2489 148 5 |678 789 46789 |124679 1279 3 349 6 149 |2 3579 34579 |1479 8 1459 7 348 2489 |3568 3589 1 |2469 259 24569

floors1357 permutations =93

Code: Select all: N:.................................................XX.............................. R:.XXXXXXX..........XX.XXX.XX.........XX.XXX.XX..........XXXXXXX................... C:.XXXX.XXX.........XX.XXXXX..........XX.XXX.XX..........XXXXXXX................... B:.XXXXXX.X..........XXXXXXX..........XX.XXX.XX.........XX.XXX.XX.................. 1 2 3 4 5 6 7 8 9 NE..................................x..x...........................................

You should find something to clear nodes N48 and N52 using a sub group of the above group of sets
N48<>2 N52<>8

Code: Select all: 003010005020400000100000700040806000000049060002000000007000100080900020500000003 col809# 92145

Code: Select all: 46789 679 3 |267 1 278 |24689 489 5 6789 2 5689 |4 356789 3578 |3689 1389 1689 1 569 45689 |2356 235689 2358 |7 3489 24689 ----------------------------------------------------------- 379 4 159 |8 2357 6 |2359 13579 1279 378 1357 158 |12357 4 9 |2358 6 1278 36789 135679 2 |1357 357 1357 |34589 1345789 14789 ----------------------------------------------------------- 2 369 7 |356 3568 3458 |1 4589 4689 346 8 146 |9 3567 13457 |456 2 467 5 169 1469 |1267 2678 12478 |4689 4789 3

floors1357 permutations =11

Code: Select all: N:.....................................X..........XXX.............................. R:.X.XXX.XX..........XXXXXXX...........XXXXXXX..........XX.XXX.XX.................. C:.XXX.X.XX.........XX.XXXXX...........XXXXXXX..........XX.XXX.XX.................. B:..XXXXXX...........XXXXXXX..........XX.XXX.XX.........XX.XXX.XX.................. 1 2 3 4 5 6 7 8 9 NE.............xx.x.................x....x...........................xx............

Code: Select all: 1: r5c3r6c9r9c3 3: r3c56r4c5r6c1678r7c45 5: r3c356r4c5r6c27r7c5 7: r1c16r4c5r6c129r8c6r9c5

I think this puzzle is over valued in my process. As you can see, a group of the same floors offers wider possibilities(if there is no bug in the program).
7 nodes can be cleared (only 1;3;5;7 valid)
nearly as many potential eliminations that in Fata Morgana for candidates 1;3;5;7

Code: Select all: 000000039000001005003050800008090006070002000100400000009080050020000600400700000 Golden Nugget

Code: Select all: 25678 14568 124567 |268 2467 4678 |1247 3 9 26789 4689 2467 |23689 23467 1 |247 2467 5 2679 1469 3 |269 5 4679 |8 12467 1247 --------------------------------------------------------- 235 345 8 |135 9 357 |123457 1247 6 3569 7 456 |13568 136 2 |13459 1489 1348 1 3569 256 |4 367 35678 |23579 2789 2378 --------------------------------------------------------- 367 136 9 |1236 8 346 |12347 5 12347 3578 2 157 |1359 134 3459 |6 14789 13478 4 13568 156 |7 1236 3569 |1239 1289 1238

floors1247 permutations =80

Code: Select all: N:......X........X..........X.......X.............................................. R:X.XXX.XXXXXXX.XX.X.........XXXXX.XX...................XXXX.XXX................... C:.XXXX.XXXX.XXX.XXX..........XX.XXXXX..................X.X.XXXXX.................. B:X.X.XXXXXXXXX.X.XX.........XXXX.X.XX..................XXX.XXX.X.................. 1 2 3 4 5 6 7 8 9 NE..............................................................x..................

As you see, the response for GN is limited to the possibility to clear N79 using floors 1247

I can do more if this is of interest for you