The New Sudoku Players' Forum

by **Allan Barker** » Sun Nov 16, 2008 5:18 am

denis_berthier wrote:Two questions.
1) Could you define more precisely what you call an "SK-like loop", especially if there is no symmetry in the pattern. Your description evokes less a loop than some central cell with petals.
I gave two different interpretations of the "SK-loop", here: http://forum.enjoysudoku.com/viewtopic.php?t=5894
Anyway, if there appears to be an interpretation of the "SK-loop" more general than mine, whatever it is, I'm interested if it can be described in terms of factual patterns.

You bring up a good point, which I remember you mentioning before. I have used the term SK-like to describe a family of similar structures found at the beginning of monster solutions. Some, Like Tungsten Rod and Fata Morgana, may have cells in addition to loopishness. I'm sure they could be described in terms of a group of factual patterns, the question is how many patterns, maybe not so many. Maybe we could try to make one for FM first?

The common property seems to be they are all, or part rank 0 logic. Candidates are eliminated from rank 0 sets like in continuous nice loops and I would put them in a broad logic family that included CNLs. They are logically similar but more complex. They have a variety of geometries including petals or figure 8s. Granted, there needs to be a better term.

Although the Top1465 #2 structure does not look much like a loop in rcn space, the logical strucure does. Here is a sligtly permuted version of the logic.

Code: Select all: 7c7 2n8 2n9 5c5 9b5 5n6 5n3 5n2 6n2 9n2 8b7 1r7 2r7 7R2: 727==728==729 | | | 8R2: | 828==829 | | | 5R2: | 528==529==525 | | 4N5: | 545==945 | | | 9R5: | | 956A=956A=953 | | 954 | | | | | | 2R5: | | 256==253==252 | | | | | 6R5: | | 656==653==652 | | | 7C2: | | 752==762==792 | | | | 5C2: | | 562==592 | | | | 8C2: | | 862==892B=892B | | 882 | | | 7N1: | | 871==171==271 | | | | 7N5: | 575=====================================175==275 | | | 7N7: 777====================================================177==277

denis_berthier wrote:2) Second question. ttt gave another, apparently much simpler, solution in the "abominable T&E" thread. What do you think of it?

Yes, I saw that, as usual ttt's solutions are excellent. As for size, his first elimination uses 9 sets and 11 cover sets thus his overall solution is larger, and of course doesn't eliminate 31 candidates.

denis_berthier wrote:do you know why your solver didn't find it?

Actually, my solver did find the same elimination with slightly smaller logic using 8 sets and 10 cover sets.
However, I thought blasting an entire monster at once was more interesting.
:!:

by **Allan Barker** » Sun Nov 16, 2008 6:13 am

ronk wrote:
denis_berthier wrote:1) Could you [edit: Allan Barker] define more precisely what you call an "SK-like loop", especially if there is no symmetry in the pattern. Your description evokes less a loop than some central cell with petals.

A "best symmetry" isomorph of the top1465 #2 is ...
Code: Select all
7 . 8 | . . . | 3 . . . . . | 2 . 1 | . . . 5 . . | . . . | . . . -------+-------+------- . 4 . | . . . | . 2 6 3 . . | . 8 . | . . . . . . | 1 . . | . 9 . -------+-------+------- . 9 . | 6 . . | . . 4 . . . | . 7 . | 5 . . . . . | . . . | . . . top1465 #2 . . . | . . . | . . . . 7 . | . . . | . . 5 . . 6 | . . 9 | . 4 . -------+-------+------- . . . | . 5 . | . . . . . . | 8 7 . | . . 3 1 . 2 | . . . | . . . -------+-------+------- . . . | . . 4 | 2 6 . . . 1 | . . . | 9 . . . 8 . | . 3 . | . . . top1465 #2 isomorph permutation: -pr(159)(268)(347)c(1526)(34)(798)

Allan, I would like to see the 2-D grid drawing for your "SK-like loop" deduction in this isomorph. Assuming you have the time, thanks in advance.

Ronk, as requested, Allan

Thumb 2D grid drawing Top1465 #2 isomorph.

by **champagne** » Sun Nov 16, 2008 6:43 am

Allan Barker wrote:I do see several shorter eliminations but found this one after searching around a bit. I was quite surprised to see 31 eliminations, so I focused on this elimination

By "lock" you mean that the simpler solutions prevent the solver from finding more complex eliminations, right? I often see this, too.

What surprised me here is to have a very small SLG for so many eliminations. Likely a specificity behind, but I did not investigate

“prevent” is not the appropriate term. A strategy has to be applied when searching paths for a solution. My standard strategy is more or less “do first what appears first”. I have another option which is “do first what will give an immediate assignment”. Why not “search for the biggest number of eliminations” or “search for one shot if possible”.

Allan Barker wrote:Yes, I am looking for any path, as opposed to starting with floors. To the solver, multiple digits in a row/column are the same as one digit in several rows/columns. Of course, any is not the same as every.

I am not so sure there is opposition between these two strategies. I am confident that in most cases simple paths will get out of a small number of floors. The search mode is just a question of time. Nothing prevents to make a first overview looking for example for the most efficient combinations of floors.

Allan Barker wrote:
champagne wrote:For sure, you can find corresponding SLG's, but both are using AHS/ACs and I don't know yet how it is translated in SLGs

This is an interesting point. In principle, there must be a (constraint) set description for any elimination path. However, a rule may embody this in various ways. Compared to computer languages, a rule might be C language and the 324 constraints would be assembly language. (?)

You have examples using ALS. It is exactly the same underlying logic, I did not study them, but I can guess that to have an equivalent SLG you have to introduce digits having a neutral effect in AIC’s crossing ALS or AHS/ACs .

champagne

by **Allan Barker** » Sun Nov 16, 2008 6:55 pm

Allan Barker wrote:
denis_berthier wrote:do you know why your solver didn't find it?

Actually, my solver did find the same elimination with slightly smaller logic using 8 sets and 10 cover sets. (Edit: 9 cover sets)

Here are two such solutions. The first is a rank 1 chain-like strucutre that eliminates the candidates by overlap of a cover set with the cover sets of an ALS. The second has a triplet (weak corner) that promotes the rank of cover set 7r5 to 0, thus eliminating all 3 candidates. Note:cover set = linkset.

Code: Select all: Top1465 #2, Eliminates 3 Candidates 7r5c236 Overlap of two linksets E99 23 Nodes, Raw Rank = 1 (linksets - sets) 8 Sets = {5r2 269r5 7c89 4n5 8b3} 9 Links = {7r5 5c5 2n89 5n236 9b5 7b9} --> (7r5*5n2) => r5c2<>7, (7r5*5n3) => r5c3<>7, (7r5*5n6) => r5c6<>7 7r5 7b9 2n9 2n8 5c5 9b5 5n6 5n3 5n2 7C8: 758==778=======728 | 798 | | | | 7C9: 759==799==729 | | | | 8B3: | 829==828 | | | 5R2: | 529==528==525 | | 4N5: | 545==945 | | 9R5: | 956A=956A=953 } | 954 | | } | | | } ALS in rows 6R5: | 656==653==652 } ie, 3 rows in 4 cols | | | | } 2R5: | 256==253==252 } | | | | ............................................................... | | | | +--------------------------> 756 753 752 Eliminate

Code: Select all: Top1465 #2, Eliminates 3 Candidates 7r5c236 Rank 0 Linkset becasue of triplet B, E99 23 Nodes, Raw Rank = 1 (linksets - sets) Link set 7r5 = Rank 0 8 Sets = {578r2 4r6 8c7 4n5 5n4 7b6} 9 Links = {7r5 5c5 7c7 2n89 4n7 6n7 49b5} --> (7r5) => r5c2<>7, (7r5) => r5c3<>7, (7r5) => r5c6<>7 2n8 2n9 5c5 9b5 7r5 4b5 6n7 4n7 7c7 7R2: 728==729================================727 | | | 8R2: 828==829 | | | | 5R2: 528==529==525 | | | 4N5: 545==945 | | | 5N4: 954==754==454 | | | | 4R6: | 465==467 | | 466 | | | | | 8C7: | 867==847 | | | | | 7B6: 757B======767C=747A=747A 758 757B 759 767C ............................................................. | 752 } 753 } Eliminate 756 } ^Rank 0 cover set Notes 1) A, B, C indicate candidate in multiple cover sets 2) Vertical adjoining candidates indicate box/line link (hinge)

Website · by **denis_berthier** » Sun Nov 16, 2008 9:10 pm

Allan Barker wrote:
ronk wrote:
denis_berthier wrote:1) Could you [edit: Allan Barker] define more precisely what you call an "SK-like loop", especially if there is no symmetry in the pattern. Your description evokes less a loop than some central cell with petals.

A "best symmetry" isomorph of the top1465 #2 is ...
Code: Select all
. . . | . . . | . . . . 7 . | . . . | . . 5 . . 6 | . . 9 | . 4 . -------+-------+------- . . . | . 5 . | . . . . . . | 8 7 . | . . 3 1 . 2 | . . . | . . . -------+-------+------- . . . | . . 4 | 2 6 . . . 1 | . . . | 9 . . . 8 . | . 3 . | . . .

Allan, I would like to see the 2-D grid drawing for your "SK-like loop" deduction in this isomorph.

Ronk, as requested, Allan
Thumb 2D grid drawing Top1465 #2 isomorph.

Allan, thanks for this 2D view.
It is so complex that I'm not sure this should be called an SK-loop.

by **champagne** » Mon Nov 17, 2008 12:51 am

Hi Allan,

I had a look to your diagram eliminating 7r5c236.

My AIC was

7r5c236 - 9r5c36 AC:(r5c236) = 9r5c4 - 9r4c5 = 5r4c5 - 5r2c5 = 5r2c89 - 7r2c89 AC:(r2c89) = 7r2c7 - 7r456c7 = 7r5c89 - 7r5c236

where AC:(r5c236) shows that the weak link comes from the AC r5c236.

If I am right, the corresponding SLG would be

Code: Select all: 758;759 ========= 747;757;767 box 6 is a set | | column c7 is a linkset | 729==728=== 727 | | | 8B3: | 829==828 | | | 5R2: | 529==528==525 | | 4N5: | 545==945 | | 9R5: | 956A=956A=953 } | 954 | | } | | | } ALS in rows 6R5: | 656==653==652 } ie, 3 rows in 4 cols | | | | } 2R5: | 256==253==252 } | | | | ............................................................... | | | | +--------------------------> 756 753 752 Eliminate

very close to yours.
I see in a better way now how to switch from an AIC to a SLG.

All sets are strong inferences
All linksets are weak inferences.

And each local weak link should have a corresponding sets linksets pattern.

No surprise, your translation from ALS_ACS to sets is easier if you look at the AC.
The sets you add are the sets creating the AC pattern.

by **Allan Barker** » Tue Nov 18, 2008 5:36 am

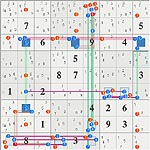
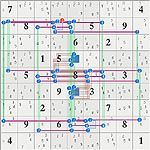
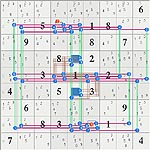
Another difficult puzzle with FM type loop

tarx0075 from HERE(pointed out by ttt)

FM first loop summary . The first FM loop had 2 central-box strong cell-sets, surrounded by 3 identical layers, one of the layers was anti-symmetric wrt the other two. The anti-symmetry was required (for that logical design) to cause the elimination. Making all 3 layers symetrical prevented the eliminations.

This puzzle's initial loop is similar (same family) but larger with more complex symmetry. It has 4 layers and only the bottom 3 are the same. Among the bottom 3 layers there are 2 r 3 different symmetries, reflecting the symmetry of the puzzle. The top layer, layer 4, also has a broken symmetry in the puzzle.

Studying the symmetry of the assigned cells could help a solver find such loops, since they have the same symmetry

So far there are two styles, first type:

Layer 4 diff. 3 row sets
Layer 6 same 2 rows, 1 column, 1 box -normal-
Layer 7 same 2 rows, 1 column, 1 box -rotation-
Layer 9 same 2 rows, 1 column, 1 box -reflection-

Second type:

Layer 4 diff. 3 row sets
Layer 6 same 2 rows, 2 column -normal-
Layer 7 same 2 rows, 2 column -normal-
Layer 9 same 2 rows, 2 column -reflection-

The common theme seems to be large, symmetrical, layered, loopish structures that eliminate their candidates by rank 0 linksets (cover sets), like continuous nice loops. Not all linksets need be rank 0. The other property is they only appear in the initial part of the solution path.

Column/Box type loop:

Code: Select all: +-----------------------------------------------------------------------------+ | 1238 123478 124(7) | 2479 234579 4579 | 3459 12345 6 | | 23(6) 23(47) 5 | 2(4679) 23(4679 1 | 8 23(4) 23(9) | | 1236 9 1246 | 246 23456 8 | 345 7 1235 | +-----------------------------------------------------------------------------+ | 159(6) 157 1(679) | 8 (4679) 2 | 345(679 13456 135(79) | | 589(6) 578 3 | 679(4) 1 679(4) | 2 568(4) 58(79) | | 4 1278 12(679) | 5 (679) 3 | (679) 168 18(79) | +-----------------------------------------------------------------------------+ | 1235 6 124 | 1247 24578 457 | 357 9 23578 | | 25(9) 25(4) 8 | 3 25(4679 5(4679) | 1 25(6) 25(7) | | 7 1235 12(9) | 1269 25689 569 | 35(6) 23568 4 | +-----------------------------------------------------------------------------+

Set Logic Elimination, column box type:

Code: Select all: RABX 58 Nodes, Raw Rank = 5 (linksets - sets) 17 Sets = {4679r2 4r5 4679r8 79c3 6c7 46n5 6b4 79b6} 22 Links = {679r4 679r6 6c1 4c2 4679c5 4c8 79c9 2n4 8n6 7b1 4b5 39b7 6b9} --> (2n4) => r2c4<>2, (8n6) => r8c6<>5

Thumbs to images: left: 2D grid images (2 loops), right 3D jiggle pic.
(the right 3D image is meant to jiggle to give a sense of depth)

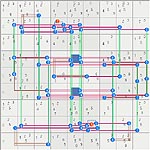
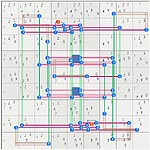
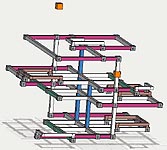Logic Diagram Column/Row type loop:

Code: Select all: 2n4 8n6 4c2 4c5 4c8 4b5 6c5 6b1 6r6 6r4 6b9 7c5 7b9 7r4 7r6 7b1 9c5 9b7 9r4 9r6 9b3 6R8: 686======================685=================688 | | | 6R2: 624===|=======================625==621 | | | | | | 6C3: | | | 633==663==643 | | | | | | | 6C7: | | | 667==647==697 4R2: 424===|===422==425==428 | | | | | | | | | | | 4R8: | 486==482==485 | | | | 4R5: | | | 458==454 | | | | | | 456 | | | 6N5: | | | | 665E======665E==|========765F===========765F======965G===========965G | | | | | | | | | | 4N5: | | 445A======445A=645B===========645B======745C======745C==|========945D======945D | | | | | | | | | 7C7: | | | 777==747==767 | | | | | | | | | | | | 7C3: | | | | 743==763==713 | | | | | | | | | | | 7R8: | 786===============================================785==789 | | | | | | | | | | | 7R2: 724===|================================================725=================722 | | | 9C3: | | | 993==943==963 | | | | | | 9C7: | | | | 947==967==917 | | | | | 9R8: | 986========================================================================985==981 | | | | 9R2: 924=============================================================================925=================929

Logic Diagram Column/Box type loop:

Code: Select all: 4c8 4b5 4c5 4c2 8n6 6b9 6r4 6r6 6c1 6c5 7c5 7c9 7r4 7r6 7b1 9c5 9b7 9r4 9r6 9c9 2n4 4R2: 428=======425==422==================================================================================424 | | | | 4R5: 458==454 | | | 456 | | | 4R8: | 485==482==486 | | | | | 6R8: | | 686==688=================685 | | | | | | | 6C7: | | | 697==647==667 | | | | | | | | | 6B4: | | | 641A=663==641A | | | | | 643 | 651 | | | | | | | | | | 6R2: | | | | | 621==625====================================================624 | | | | | | | 6N5: | | | | 665H======665H=765I===========765I======965J===========965J | | | | | | | | | | | 4N5: 445B=445B=======|========645C===========645C=745D======745D==|========945E======945E | | | | | | | | | | 7R8: 786===========================785==789 | | | | | | 7C3: | | | 743==763==713 | | | | | | | | | | | | | | 7B6: | | 749F=749F=769K | | | | | | | 759K 747 767 | | | | | | | 769 | | | | | 7R2: | 725=================722===|=========|====|========724 | | | | | 9R8: 986====================================================985==981 | | | | | | | | 9C3: | 993==943==963 | | | | | 9B6: | 949G=969L=949G | | 947 967 959L | | 969 | | | | 9R2: 925=================929==924 Notes 1) A, B, C indicate candidate in multiple cover sets 2) Vertical adjoining candidates indicate box/line link (hinge)

.

by **Allan Barker** » Fri Nov 21, 2008 5:08 pm

ttt here in wrote:I’m still thinking…
For patterns you suggested, I don’t know. I thought simple that if we have two strong sets A=B & C=D => at least one of [(A&C), (A&D), (B&C), (B&D)] must be true then the effect is difference with we use A=B, C=D separate. Back to the puzzle with my last post then we have 4 “true” in the same time, based on that I found r46c3<>1, presenting it is not nice and I’m still thinking more, hope find something…
ttt

ttt, following your thinking, I find the following i-loop(initial loop). It is similar but smaller than the previous ones for tarx0075(above), It uses 3 of your dual- strong-infrence sets in rows 258. These connect through 2 more sets in the central box. I think this the most pure form of the design.

Champagne, I have now found about 8 varients. As far as convergence, all searches converge on this 'group' of patterns however they will converge to slightly different varients.

Thumbs to images: 2D grid image of "All Rows" solution

Code: Select all: RABZ 47 Nodes, Raw Rank = 4 (linksets - sets) 14 Sets = {4679r2 4679r5 4679r8 46n5} 18 Links = {69c1 47c2 4679c5 46c8 79c9 2n4 8n6 4679b5} --> (2n4) => r2c4<>2, (8n6) => r8c6<>5 +-----------------------------------------------------------------------------+ | 1238 123478 1247 | 2479 234579 4579 | 3459 12345 6 | | 23(6) 23(47) 5 | 2(4679) 23(4679 1 | 8 23(4) 23(9) | | 1236 9 1246 | 246 23456 8 | 345 7 1235 | +-----------------------------------------------------------------------------+ | 1569 157 1679 | 8 (4679) 2 | 345679 13456 13579 | | 58(69) 58(7) 3 | (4679) 1 (4679) | 2 58(46) 58(79) | | 4 1278 12679 | 5 (679) 3 | 679 168 1789 | +-----------------------------------------------------------------------------+ | 1235 6 124 | 1247 24578 457 | 357 9 23578 | | 25(9) 25(4) 8 | 3 25(4679 5(4679) | 1 25(6) 25(7) | | 7 1235 129 | 1269 25689 569 | 356 23568 4 | +-----------------------------------------------------------------------------+

Code: Select all: 4c8 4b5 4c2 4c5 6c1 6b5 6c8 6c5 2n4 8n6 7c9 7c5 7c2 7b5 9c9 9c5 9c1 9b5 4R8: 482==485===========================486 | | | 4R2: 428=======422==425======================424 | | | | | 4R5: 458==454 | | | 456 | | | | | | | 6R2: | | 621============625==624 | | | | | | | 6R8: | | | 688==685===|===686 | | | | | | | 6R5: | | 651==654==658 | | | |__ ___| 656 | | | \ / | | | | 4N5: 445=============|===645===|====|====|=============745=================945 |__/ \__| | | __/ \__ __/ \__ \ / | | | \ / | | \ / | 6N5: 665========|====|=========|===765===|==========|==965 | | | | | | | 7R2: 724===|========725==722 | | | | | | | | | | 7R8: | 786==789==785 | | | | | | | | | | | 7R5: | | 759=======752==754 | | | | 756 | | | | | | 9R8: | 986===========================985==981 | | | | | 9R2: 924===========================929==925 | | | | | 9R5: 959=======951==954 956

by **champagne** » Fri Nov 21, 2008 11:03 pm

Hi Allan,

I am very surprised than you can't do anything out of my group of sets.

I revised the design to be closer to yours, and herebelow is the final status.

It is very similar to FM first loop, so I thought you would have no problem to establish the left part of the diagram is rank 0.

It is still out of my skills, but again, it is so close to FM first loop that I think it should be.

If not, could you explain why and how you account rank in such a diagram.

As I wrote before, the proposal of the solver is slightly different, but I was confident that such a diagram having a best symmetry would be equivalent.

Code: Select all: 18 sets N45 N65 4679C3467 22 Linksets 4679B5 4R1347 6R3469 7R1467 9R1469 N24 N86 rank 4 7 triple points all linksets form N24 N86 4B5 4R4 4R1 4R3 4R7 <== 7 linksets | | | | | | | 4c7 ============= 447 417 437 | 4c3 ================= 413 433 473 4c6 | 486 456 ====== 416 436 | 7 triples points in sets N45 N65 4c4 424 | 454 ===== 414 434 474 V V V V | | | | N45 | | 445A 445A === 645B 645B =============745C 745C=========== 945D 945D | | | | | | | | | N65 | |=========== 665b | 665b==============765c ====765c ====== 965d= |= 965d | | | | | | | | | | 6c4 624 | ========== 654 ==|====|===|==634 | | | | | | 6c6 | 686 =============== 656 ==|===|===|== 696 | | | | | | 6c3 | | ==================== 643 663 633 | | | | | | 6c7 | | ==================== 647 667==|===697 | | | | | | | | | | | | | | | | | | | 7c4 724 | =================|====|===|===|===|== 754 | | 714 774 | | | 7c6 | 786 =================|====|===|===|===|== 756 | | 716 776 | | | 7c3 | | =================|====|===|===|===|====|===743 763 713 | | | | 7c7 | | =================|====|===|===|===|====|===746 766 | | | | | | | | | | | | | | | | | | | | 9c4 924 | =================|====|===|===|===|====|====|===|===|===|== 954 | | 914 994 9c6 986 =================|====|===|===|===|====|====|===|===|===|== 956 | | 916 996 9c3 =========================|====|===|===|===|====|====|===|===|===|== | 943 963 | 993 9c7 =========================|====|===|===|===|====|====|===|===|===|== | 947 967 917 | | | | | | | | | | | | | | | 15 linksets 6B5 6R4 6R6 6R3 6R9 7B5 7R4 7R6 7R1 7R7 9B5 9R4 9R6 9R1 9R9

by **Allan Barker** » Sun Jan 04, 2009 2:12 am

Identical Loops in Tarek-0075 and Golden Nugget Morph
Comparison with Fata Morgana Loop

I looked more closely at morphs of Golden Nugget and was surprised to find the same loop (identical logical form) as from the inital loop from tarek-0075. These loops are similar to ones found in other puzzles like Fata Morgana, and. have alternate logical forms depending on how the central box is connected.

I placed a logic diagram for Fata Morgana at the bottom for comparison. It looks like FM only differs because it is missing the top layer (relative to the diagram) of the other two puzzles. The top layers of Tarek-75 and GN are different from the other layers and has the only bi-value set in the logic.

Golden Nugget Morph Summary

ENMA 47 Nodes, Raw Rank = 4 (linksets - sets)
14 Sets = {1247R2 1247R5 1247R8 46N5}
18 Links = {12c1 47c3 1247c5 14c7 27c9 2n4 8n6 1247b5}
--> (2n4) => r2c4<>3[/code]

.Thumbs Left: Golden Nugget Morph, Right: Tarek-0075.

Code: Select all: Golden Nugget Morph, Initial Loop, notation is NCR +--------------------------------------------------------------------------------------+ | 7 1236 3569 | 1238 1239 1289 | 13568 156 4 | | 36(12) 8 36(4) | -3(1247) 3(1247) 5 | 36(1) 9 36(7) | | 1359 134 3459 | 13478 6 14789 | 2 157 3578 | +--------------------------------------------------------------------------------------+ | 23689 23467 1 | 5 (247) 2467 | 4689 2467 26789 | | 69(2) 5 69(47) | (1247) 8 6(1247) | 69(14) 3 69(27) | | 268 2467 4678 | 9 (1247) 3 | 14568 124567 25678 | +--------------------------------------------------------------------------------------+ | 13568 136 2 | 1348 13459 1489 | 7 456 3569 | | 35(1) 9 35(7) | 6 35(1247) (1247) | 35(4) 8 35(2) | | 4 367 35678 | 2378 23579 2789 | 3569 256 1 | +--------------------------------------------------------------------------------------+ 4c8 4b5 4c2 4c5 6c1 6b5 6c8 6c5 2n4 8n6 7c9 7c5 7c2 7b5 9c9 9c5 9c1 9b5 4R8: 482==485===========================486 } | | | } 4R2: 428=======422==425======================424 | } "Top" Loop | | | | } 4R5: 458==454 | | | } 456 | | | 6R2: | | 621============625==624 | | | | | | | 6R8: | | | 688==685===|===686 | | | | | | | 6R5: | | 651==654==658 | | | | | 656 | | | | | | | | | 4N5: 445A======445A======645B======645B==|====|========745C======745C======945D======945D | | | | | | | | 6N5: 665E======665E==|====|========765F======765F======965G======965G | | | | | | 7R2: 724===|========725==722 | | | | | | | | | | 7R8: | 786==789==785 | | | | | | | | | | | 7R5: | | 759=======752==754 | | | | 756 | | 9R8: | 986===========================985==981 | | | | | 9R2: 924===========================929==925 | | | | | 9R5: 959=======951==954 956 Tarek-0075, Initial Loop, notation is NCR 1c7 1b5 1c1 1c5 2c1 2b5 2c9 2c5 2n4 8n6 7c5 7c3 7c9 7b5 4c3 4c5 4c7 4b5 1R8: 181==185===========================186 } | | | } 1R2: 127=======121==125======================124 | } "Top" Loop | | | | } 1R5: 157==154 | | | } 156 | | | 2R2: | | 221============225==224 | | | | | | | 2R8: | | | 289==285===|===286 | | | | | | | 2R5: | | 251==254==259 | | | | | 256 | | | | | | | | | 6N5: 165D======165D======265E======265E==|====|===765G===========765G======465F======465F | | | | | | | | 4N5: 245A======245A==|====|===745C===========745C======445B======445B | | | | | | 7R2: 724===|===725=======729 | | | | | | | | | | 7R8: | 786==785==783 | | | | | | | | | | | 7R5: | | 753==759==754 | | | | 756 | | 4R8: | 486===========================485==487 | | | | | 4R2: 424===========================423==425 | | | | | 4R5: 453=======457==454 Fata Morgana, Initial Loop, notation is NCR 1r1 1b5 1r9 1r5 6n8 4n2 3r5 3r9 3r2 3b5 6r8 6r5 6r1 6b5 <------- (missing top loop) 1C8: 118============158==168 | | | 1C2: | 192==152===|===142 | | | | | 1C5: 115==145==195 | | | 165 | | | | | | | 5N4: 154A======154A==|====|===354B===========354B======654C======654C | | | | | | | | 5N6: 156D======156D==|====|===356E===========356E======656F======656F | | | | | | 3C2: | 342==352=======322 | | | | | | | | | | 3C8: 368===|===358==398 | | | | | | | | | | | 3C5: | | 395==325==345 | | | | 365 | | 6C2: | 642===========================652==612 | | | | | 6C8: 668===========================688==658 | | | | | 6C5: 685=======615==645 665

The New Sudoku Players' Forum

Great Monster Loops