- Code: Select all
You're not going to make me believe, for example, that the resolutions proposed in the tarek puzzles by each other are obtained the first time without having tried something else beforehand that leads to nothing or a partial result. Even if a pattern is spotted, it would be a lucky guess if it eliminates the anti-door.
your confusion the process of finding something as the trial part vs the construct as presented in its self as the "trial".
searching for anything is "trial":
building something from given parts or a list of parts which either hit true and eliminate or hit true and do nothing can also be a "trial"
the physical construct as a whole is not trial and error but its description or methodology in how it functions can be trial.
krakens as present are almost N set's joined by N-sets to form an overall deduction. {strong links simplicity or nodes}
again all coded as And else (not And) logic gates.
i have zero issues with them due to this fact.
several of the users you have named posted techniques which are known to as Forcing nets with sub-chains which are trial and error, again no issue with them as they have mentioned what they are and are trial and error eliminations.
yes trial and error can be singular candidates, but they can also Bifurcation which is what you are doing following 2 paths.
i understand exactly what you are doing, as i said before i have your method coded as my
bruteforce solving function
locate bivalves/bi-locals and project both as true on the grid and look for commonality between the two.
{I go one step further and imply the common solved cells between the two grids as true. }
it doesn't use coloring: but it helps a manual player track the links the path moves down: which is the point.
logic gates do not retain information from previous link and apply grid changes before triggering the next marker.
tracks and anti tracks do.
again, my point is the fact you use bifurcation on two points
part A : which generates the whole solution path/ or mostly a completed one / or establishes comminality
part B: generates contradictions + partial solution
and compare the two perform eliminations based on identical scenarios between the two truths.
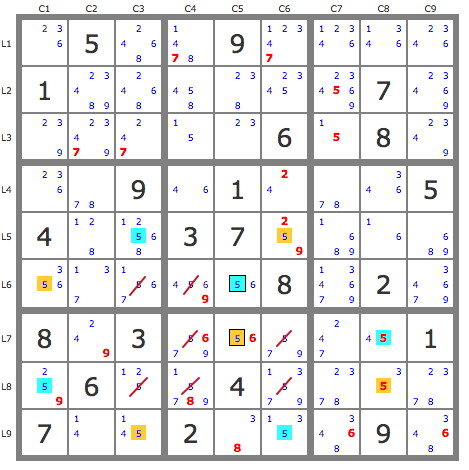
for example: (5)r7c5 = r6c5 - r6c1 = (5-9)r8c1 =(924)r7c278 => -5 r7c8; ste
- Code: Select all
+------------------------+------------------------+--------------------------+
| 236 5 2468 | 1478 9 1347 | 12346 1346 2346 |
| 1 23489 2468 | 458 238 345 | 234569 7 23469 |
| 239 23479 247 | 15 23 6 | 15 8 2349 |
+------------------------+------------------------+--------------------------+
| 236 78 9 | 46 1 24 | 78 346 5 |
| 4 128 12568 | 3 7 259 | 1689 16 689 |
| c356 137 1567 | 4569 b56 8 | 134679 2 34679 |
+------------------------+------------------------+--------------------------+
| 8 e249 3 | 5679 a56 579 | e247 e4-5 1 |
| d259 6 125 | 15789 4 13579 | 2378 35 2378 |
| 7 14 145 | 2 38 135 | 3468 9 3468 |
+------------------------+------------------------+--------------------------+
is a logic gate construct built using the given information on the grid.
your:
P'(5r7C5) : -5r7c5->[6r7c5->5r6c5->5r8c1->9r7c2]->57r7c46 => -5r7C8, stte.
the difference is you bifurcated the choice of the bivalve instead of using the links and data sets
this grid shows all the bi-locals just as your original link also does
mine on the other hand also shows the "5"'s that removed due to a N-set { fish }

- bi local grid.PNG (126.13 KiB) Viewed 866 times
heres my problem out lined:
you pick a cell which happens to be a bivalve and bi-local.
you surmised A OR B is true {which is great}
instead of writing R7C5 or R6C5 is "5" the bi-local, you instead use the bivalve for the not case. if R7C5 is not 5 then R7c5 must be 6.
then we follow the implication of the induced 6. {instead of its not 5. ie R6C5 = 5 } from their we follow the chain of 5's true/not true using induced links.
then we arrive at the switch from 5-9 {another bi-local} which leads to another switch 9(R7C2) -> 2{R7C7) then we noticed the unmarked 3 link on candidate 4 in R7C2 has 2 removed spots making it a single {but this isn't mentioned} = R7C8{4} instead we write that (57) R7C46 or that their is only 2 spots left for the 5 and apparently 7 {which also has its cell count reduced}
for here we test what if R7C5 = 5 ie R6C5 = 6 the similarities between the two is R7C8 <> 5
the whole point I'm saying is the difference in your presentation is the use of trial and error + memory chain to derive a solution:
the difference is noted above with swapping to the "5/6" from bivalves for the not case + the unnoticed 3 link on 4. and induction coloring
so again with logic gate we can build it quicker and easier without trialing both bivalves and both locations for similarities and it contains the omitted information that does the ground work for it to function:
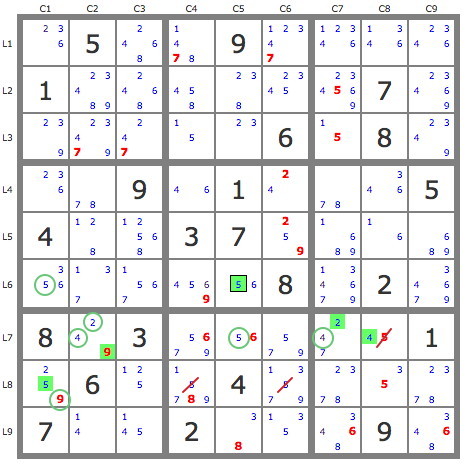
let start with the bi-local:
(5) R7C5 => R7C8 <> 5
or
( not 5 ) R7C5 = {5} R6C5 = (not 5) R6C1 = (5)R8C1 & (not 9) = (9)R7C2 [- 1 cell almost Hidden Set ] = [Hidden set] 24 R7C78 => R7C8 <> 5

- AHS.PNG (109.17 KiB) Viewed 866 times
after all that fun stuff.
instead of trialing the 56 bivalves we could have simply trialed the tipple link 4 on Row 7 and found the exact same scenarios {however it would be a three way check instead of 2}
ps: True or NoT true isn't the same as: True or True.
one examines both cases of yes or no from the same origin with out changing anything.
the other one, nope can't as it follows 2 different paths leading from both truths.
like another ? is why didn't you pick R7C8,R8C8 make this AHS
like this: {which backwards generates the other above comments}
- Code: Select all
+----------------------+-------------------+---------------------+
| 236 5 2468 | 1478 9 1347 | 12346 1346 2346 |
| 1 23489 2468 | 458 238 345 | 234569 7 23469 |
| 239 23479 247 | 15 23 6 | 15 8 2349 |
+----------------------+-------------------+---------------------+
| 236 78 9 | 46 1 24 | 78 346 5 |
| 4 128 12568 | 3 7 259 | 1689 16 689 |
| 356 137 1567 | 4569 56 8 | 134679 2 34679 |
+----------------------+-------------------+---------------------+
| 8 (249) 3 | 5679 56 579 | 7(24) (45) 1 |
| 2-5(9) 6 125 | 15789 4 13579 | 2378 3(5) 2378 |
| 7 14 145 | 2 38 135 | 3468 9 3468 |
+----------------------+-------------------+---------------------+
which is easier technically then the first method.
to me, there is a lot of ad-hock information used off the pencil-marks post induction from the path to generalize anything from your moves as its not including the
information/or information removed from via the non included cells in the overall path.